并查集(不相交集合)详解与java实现

@

目录

• 认识并查集
• 并查集解析
  • 基本思想
  • 如何查看a,b是否在一个集合？
  • a,b合并，究竟是a的祖先合并在b的祖先上，还是b的祖先合并在a上？
  • 其他路径压缩？
• 代码实现
• 结语

认识并查集

对于并查集(不相交集合)，很多人会感到很陌生，没听过或者不是特别了解。实际上并查集是一种挺高效的数据结构。实现简单，只是所有元素统一遵从一个规律所以让办事情的效率高效起来。

对于定意义，百科上这么定义的：

并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受；即使在空间上勉强通过，运行的时间复杂度也极高，根本就不可能在比赛规定的运行时间（1～3秒）内计算出试题需要的结果，只能用并查集来描述。

并查集是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。常常在使用中以森林来表示。

并查集解析

基本思想

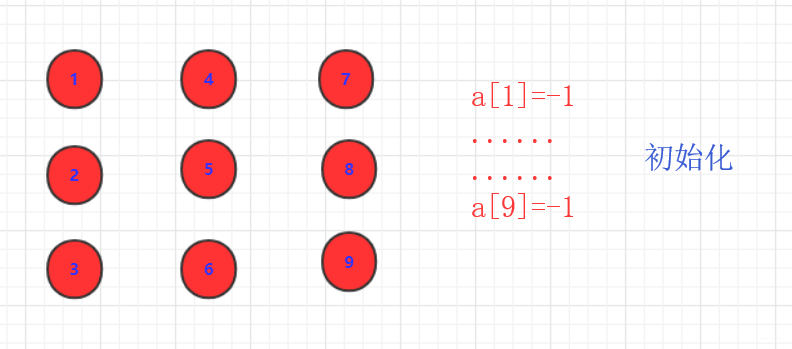
• 初始化，一个森林每个都为独立。通常用数组表示，每个值初始为-1。各自为根
  
  
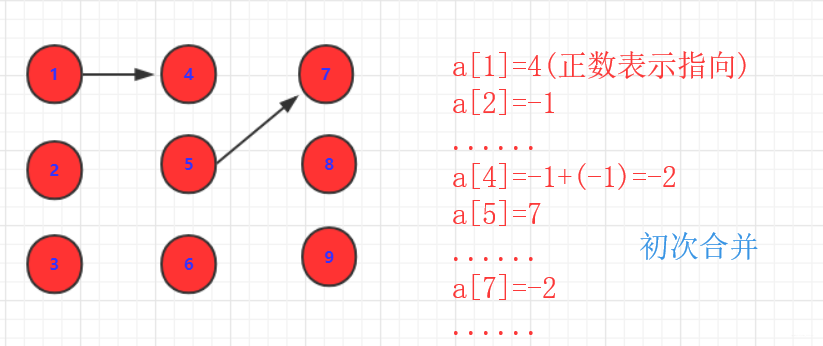
• join(a,b) 操作。a,b两个集合合并。注意这里的a，并不是a,b合并，而是a,b的集合合并。这就派生了一些情况：
• a，b如果是独立的(没有和其他合并)，那么直接a指向b(或者b指向a)，即data[a]=b;同时为了表示这个集合有多少个，原本-1的b再次-1.即data[b]=-2.表示以b为父亲的节点有|-2|个。
  
  
  
  
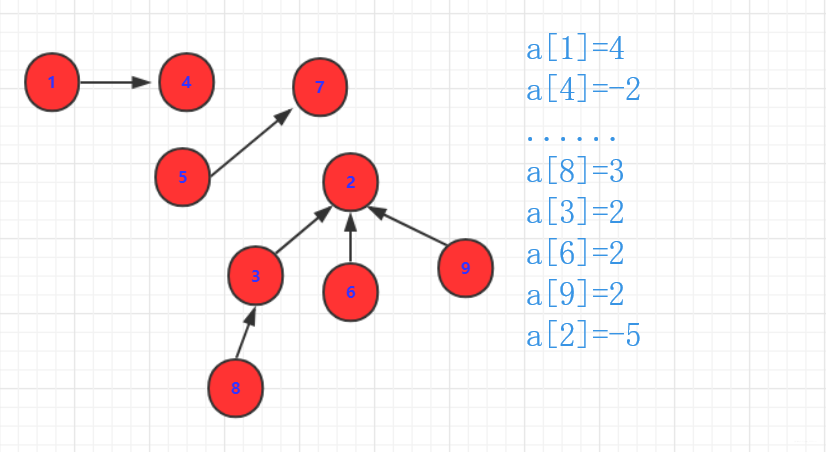
• a,b如果有集合(可能有父亲，可能自己是根)，那么我们当然不能直接操作a,b(因为a,b可能已经指向别人了.)那么我们只能操作a,b的祖先。因为a,b的祖先是没有指向的(即数据为负值表示大小)。那么他们首先一个负值要加到另外一个上面去。另外这个数值要变成指向的那个表示联系。
  
  

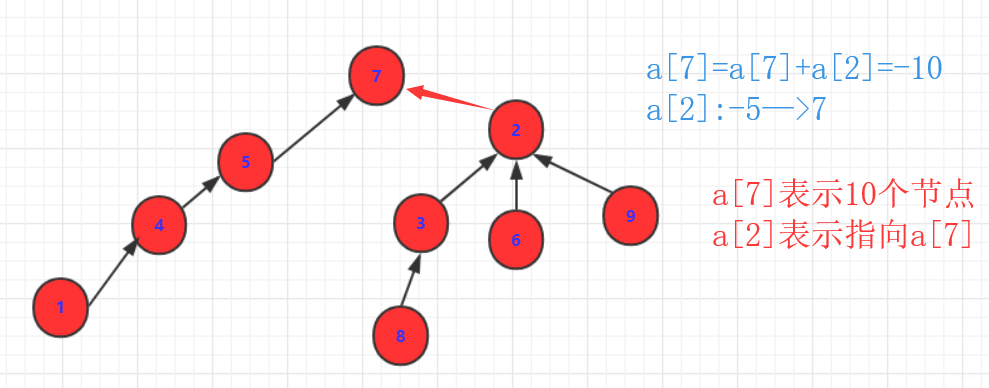
对于上述你可能会有疑问：

如何查看a,b是否在一个集合？

• 查看是否在一个集合，只需要查看节点根祖先的结果是否相同即可。因为只有根的数值是负的，而其他都是正数表示指向的元素。所以只需要一直寻找直到不为正数进行比较即可！

a,b合并，究竟是a的祖先合并在b的祖先上，还是b的祖先合并在a上？

• 这里会遇到两种情况，这个选择也是非常重要的。你要弄明白一点：树的高度+1的化那么整个元素查询的效率都会降低！

所以我们通常是：小数指向大树(或者低树指向高树)，这个使得查询效率能够增加！



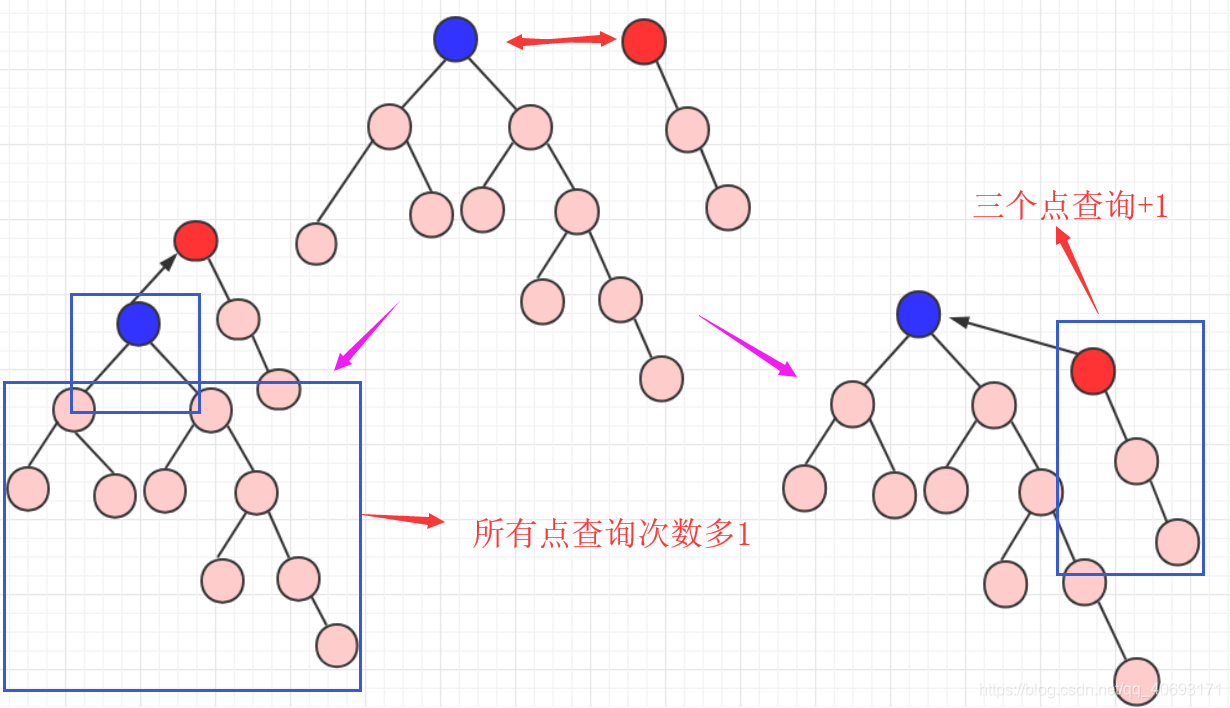
当然，在高度和数量的选择上，还需要你自己选择和考虑。

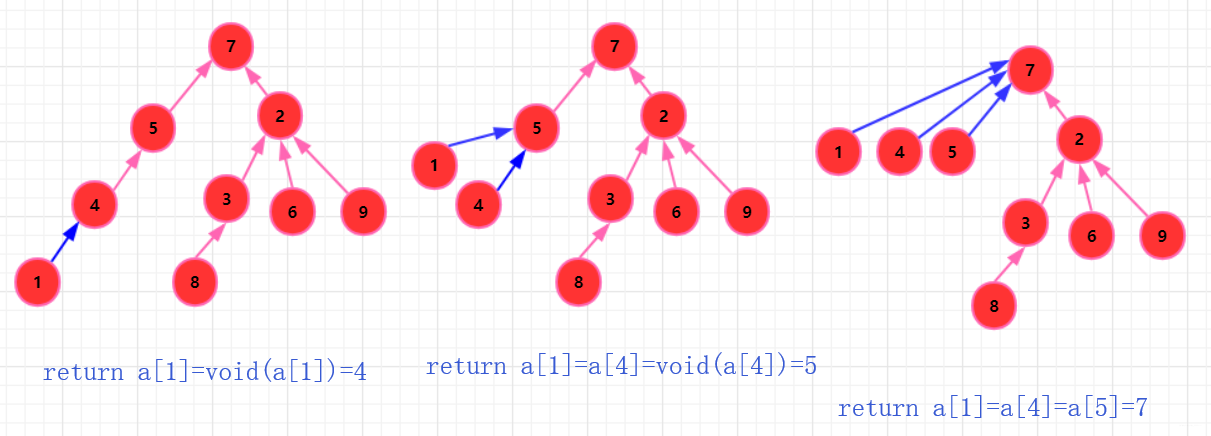
其他路径压缩？

每次查询，自下向上。当我们调用递归的时候，可以顺便压缩路径，因为我们查找一个元素其实只需要直到它的祖先，所以当他距离祖先近那么下次查询就很快。并且压缩路径的代价并不大！

代码实现

并查集实现起来较为简单，直接贴代码！

package 并查集不想交集合;

import java.util.Scanner;
public class DisjointSet {
	static int tree[]=new int[100000];//假设有500个值
	public DisjointSet() 	{set(this.tree);}
	public DisjointSet(int tree[])
	{
		this.tree=tree;
		set(this.tree);
	}
	public void set(int a[])//初始化所有都是-1 有两个好处，这样他们指向-1说明是自己，第二，-1代表当前森林有-（-1）个
	{
		int l=a.length;
		for(int i=0;i<l;i++)
		{
			a[i]=-1;
		}
	}
	public int search(int a)//返回头节点的数值
	{
		if(tree[a]>0)//说明是子节点
		{
			return tree[a]=search(tree[a]);//路径压缩
		}
		else
			return a;
	}
	public int value(int a)//返回a所在树的大小（个数）
	{
		if(tree[a]>0)
		{
			return value(tree[a]);
		}
		else
			return -tree[a];
	}
	public void union(int a,int b)//表示 a，b所在的树合并
	{
		int a1=search(a);//a根
		int b1=search(b);//b根
		if(a1==b1) {System.out.println(a+"和"+b+"已经在一棵树上");}
		else {
		if(tree[a1]<tree[b1])//这个是负数，为了简单减少计算，不在调用value函数
		{
			tree[a1]+=tree[b1];//个数相加  注意是负数相加
			tree[b1]=a1;       //b树成为a的子树，直接指向a；
		}
		else
		{
			tree[b1]+=tree[a1];//个数相加  注意是负数相加
			tree[a1]=b1;       //b树成为a的子树，直接指向a；
		}
		}
	}
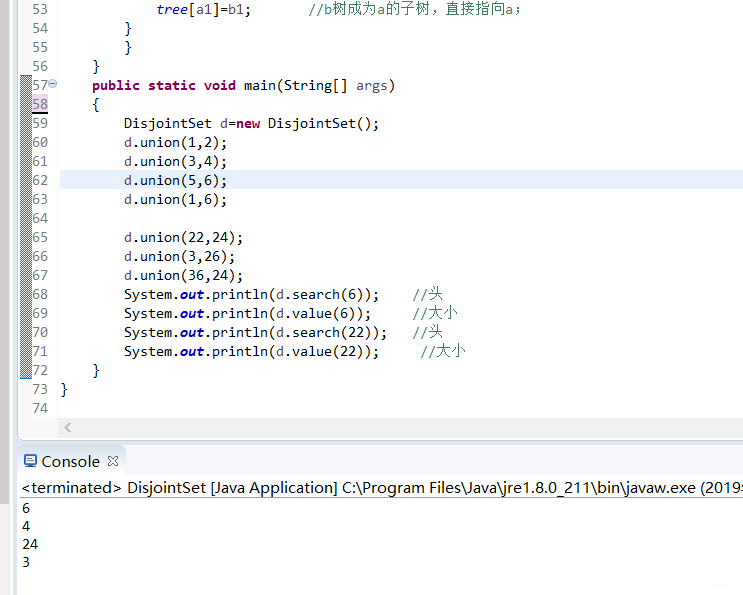
	public static void main(String[] args)
	{
		DisjointSet d=new DisjointSet();
		d.union(1,2);
		d.union(3,4);
		d.union(5,6);
		d.union(1,6);

		d.union(22,24);
		d.union(3,26);
		d.union(36,24);
		System.out.println(d.search(6));	//头
		System.out.println(d.value(6));     //大小
		System.out.println(d.search(22));	//头
		System.out.println(d.value(22));     //大小
	}
}

结语

• 并查集属于简单但是很高效率的数据结构。在集合中经常会遇到。如果不采用并查集而传统暴力效率太低，而不被采纳。
• 另外，并查集还广泛用于迷宫游戏中，下面有机会可以介绍用并查集实现一个走迷宫小游戏。大家欢迎关注！
• 最后，欢迎大家关注笔者公众号，一起学习、交流！笔者学习资源也放置公众号和大家一起分享！