【数论】【欧拉函数】bzoj2190 [SDOI2008]仪仗队

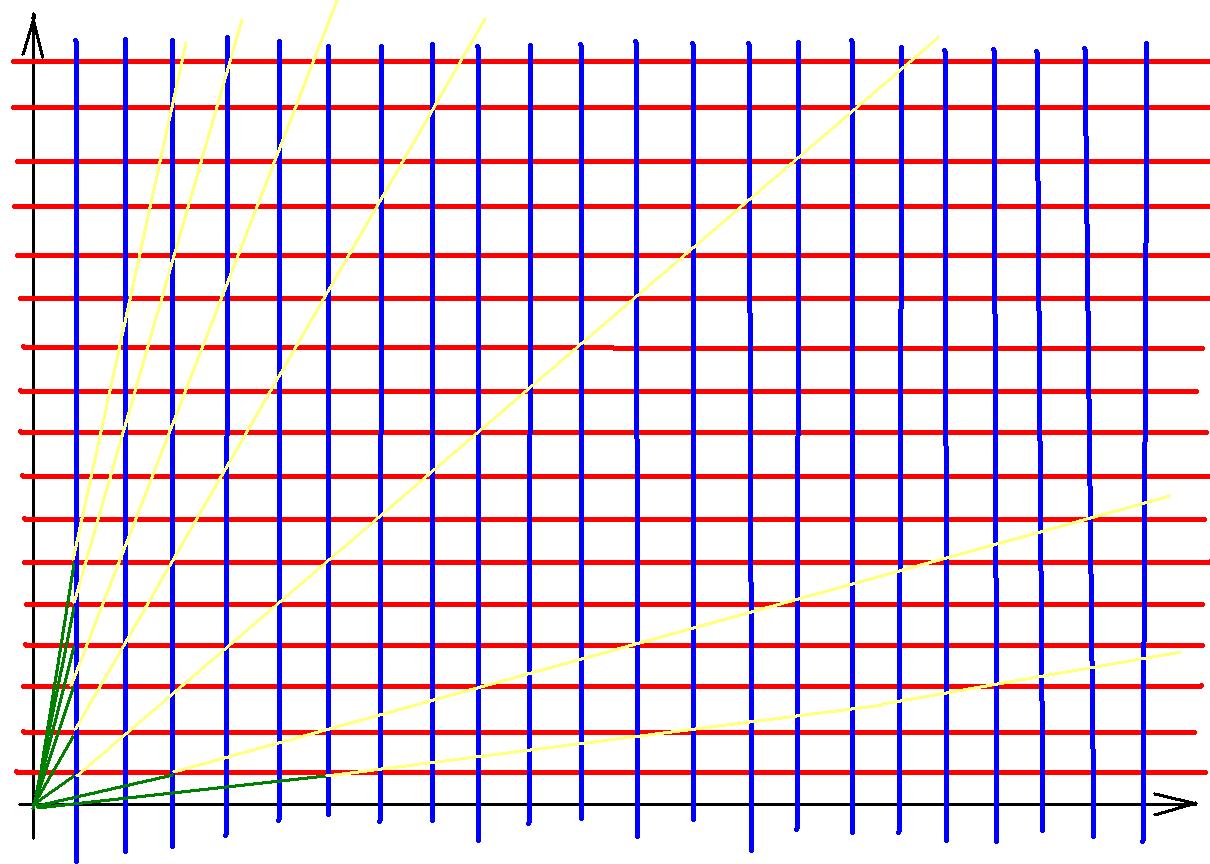
由图可知，一个人无法被看到时，当且仅当有 人与原点 的斜率与他相同，且在他之前。

∴一个人可以被看到，设其斜率为y/x，当且仅当y/x不可再约分，即gcd(x,y)=1。

考虑将图按对角线划分开，两部分对称，

对其中的下半部分来说，枚举x，其所对应的y值(y<x)有几个与它互质的，则其对答案的贡献就是几。

这个值显然就是phi(x)，所以枚举phi(x)，将它们加起来即可。

 #include<cstdio>
 using namespace std;
 int n,phi[];
 //bool get_phi(const int &x)//求单个数的phi
 //{
 //    int ans=n;
 //    for(int i=2;i*i<=x;i++)
 //      if(n%i==0)
 //        {
 //          ans=ans/i*(i-1);
 //          while(n%i==0) n%=i;
 //        }
 //    if(n>1) ans=ans/n*(n-1);
 //}
 void phi_table()
 {
     phi[]=;//规定phi(1)=1;
     for(int i=;i<=n;i++)
       if(!phi[i])//若i是质数(类似筛法的思想)
         for(int j=i;j<=n;j+=i)//i一定是j的质因数
           {
             if(!phi[j]) phi[j]=j;
             phi[j]=phi[j]/i*(i-);
           }
 }
 int main()
 {
     scanf("%d",&n);
     if(n==) printf("3\n");
     else if(n==) puts("");
     else
       {
           long long ans=;
           phi_table();
           for(int i=;i<n;i++) ans+=(long long)phi[i];
           printf("%lld\n",ans<<|);
       }
     return ;
 }