洛谷P1282 多米诺骨牌 (DP)

洛谷P1282 多米诺骨牌

题目描述

多米诺骨牌有上下2个方块组成，每个方块中有1~6个点。现有排成行的

上方块中点数之和记为S1，下方块中点数之和记为S2，它们的差为|S1-S2|。例如在图8-1中，S1=6+1+1+1=9，S2=1+5+3+2=11，|S1-S2|=2。每个多米诺骨牌可以旋转180°，使得上下两个方块互换位置。 编程用最少的旋转次数使多米诺骨牌上下2行点数之差达到最小。

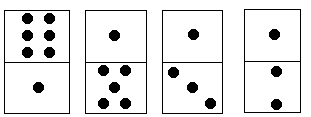
对于图中的例子，只要将最后一个多米诺骨牌旋转180°，可使上下2行点数之差为0。

输入输出格式

输入格式：

输入文件的第一行是一个正整数n(1≤n≤1000)，表示多米诺骨牌数。接下来的n行表示n个多米诺骨牌的点数。每行有两个用空格隔开的正整数，表示多米诺骨牌上下方块中的点数a和b，且1≤a，b≤6。

输出格式：

输出文件仅一行，包含一个整数。表示求得的最小旋转次数。

输入输出样例

输入样例#1：

4

6 1

1 5

1 3

1 2

输出样例#1：

1

Solution

先打了个搜索?45分

#include<bits/stdc++.h>
using namespace std;
const int N=1010,inf=2e9;
int n,tot,ans=inf,tq=inf;
int a[N],b[N];
void dfs(int x,int sum,int cnt) {
    if(x==n+1) {
        if(abs(tot-sum-sum)<ans) ans=abs(tot-sum-sum),tq=cnt;
        else if(abs(tot-sum-sum)==ans) tq=min(tq,cnt);
        return;
    }
    dfs(x+1,sum+a[x],cnt);
    dfs(x+1,sum+b[x],cnt+1);
}
int main()
{
    ios::sync_with_stdio(0);
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i]>>b[i],tot+=a[i]+b[i];
    dfs(1,0,0);
    cout<<tq<<endl;
}

为什么要贴这份代码,因为我们可以把我们搜索中记录的变量变成dp中的状态(一位dalao告诉我的做dp的方法?)

我们发现因为当题目给出塔牌的点数后,无论是否翻转,前i张牌的上下点数之和是不变的,那么我们知道一个就可以求出另一个

ok?我们现在来设计\(dp\)数组,按照搜索中的变量,设dp[i][j]表示到第i张纸牌,第一行的和为j的翻转次数

那么状态转移方程就呼之欲出了?

\(dp[i][j]=min(dp[i][j],dp[i-1][j-a[i]])\) 这是不翻转的情况

\(dp[i][j]=min(dp[i][j],dp[i-1][j-b[i]]+1)\) 翻转

我们发现这样转移可能会越界?那就加个条件嘛

  if(j-a[i]>=0) dp[i][j]=min(dp[i][j],dp[i-1][j-a[i]]);
  if(j-b[i]>=0) dp[i][j]=min(dp[i][j],dp[i-1][j-b[i]]+1);

那么初始化,第二维最大可能是6*n(每张都是6点),所以初始化

for(int i=1;i<=n;i++)
	for(int j=0;j<=6*n;j++)  dp[i][j]=inf;

然后就是dp边界

dp[1][b[1]]=1,dp[1][a[1]]=0;//为什么是这个顺序,因为如果先a后b,那么当第一张纸牌上下点数相同时,dp[1][a[1]]会被赋值成1

最后枚举一下点数统计答案就可以了,和dfs一样

Code

#include<bits/stdc++.h>
using namespace std;
const int N=1010,inf=2e5;
int n,tot,ans=inf,tq=inf;
int a[N],b[N],dp[N][6*N];
int main()
{
    ios::sync_with_stdio(0);
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i]>>b[i],tot+=a[i]+b[i];
    for(int i=1;i<=n;i++)
        for(int j=0;j<=6*n;j++)  dp[i][j]=inf;
    dp[1][b[1]]=1,dp[1][a[1]]=0;
    for(int i=2;i<=n;i++) {
        for(int j=0;j<=6*n;j++) {
            if(j-a[i]>=0) dp[i][j]=min(dp[i][j],dp[i-1][j-a[i]]);
            if(j-b[i]>=0) dp[i][j]=min(dp[i][j],dp[i-1][j-b[i]]+1);
        }
    }
    for(int i=0;i<=tot;i++) {
        if(dp[n][i]!=inf) {
            if(abs(tot-i-i)<ans)
                ans=abs(tot-i-i),tq=dp[n][i];
            else if(abs(tot-i-i)==ans) tq=min(tq,dp[n][i]);
        }
    }cout<<tq<<endl;
}

博主蒟蒻,随意转载.但必须附上原文链接

http://www.cnblogs.com/real-l/