[Python] 弗洛伊德(Floyd)算法求图的直径并记录路径

---

相关概念

对于一个图G=(V, E)，求图中两点u， v间最短路径长度，称为图的最短路径问题。最短路径中最长的称为图的直径。

其中，求图中确定的某两点的最短路径算法，称为单源最短路径算法。求图中任意两点间的最短路径算法，称为多源最短路径算法。

常用的路径算法有：

• Dijkstra算法
• SPFA算法\Bellman-Ford算法
• Floyd算法\Floyd-Warshall算法
• Johnson算法

其中最经典的是Dijkstra算法和Floyd算法。Floyd算法是多源最短路径算法，可以直接求出图中任意两点间的距离，因此只要取其中最大的就可以得到图的直径。

Floyd算法

算法思想

假设Dis(i,j)为节点u到节点v的最短路径的距离(最短路径长度)，对于每一个节点k，检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，说明从i到k再到j的路径比i直接到j的路径短，便记录Dis(i,j) = Dis(i,k) + Dis(k,j)。因此，当遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。

算法特点

• 使用了动态规划思想
• 可以计算无向图或有向图
• 核心代码简短(五行)
• 可以一次性计算出任意两点间的距离
• 算法复杂度O(n^3)，是一个好算法

一个关键性问题

在判断Dis(i,k) + Dis(k,j) < Dis(i,j)这个公式时，如果经过k的距离更短就选择k，但是这能否保证此时Dis(i,k)和Dis(k,j)已经取得了最小值呢？

答案是肯定的，可以用数学归纳法证明，参考这篇博客

示例

待求直径的图G

程序输入

2（表示无向图）

8 9 （表示8个顶点，9条边）

1 2 5 （表示顶点1和顶点2之间的距离权重是5）

... ...

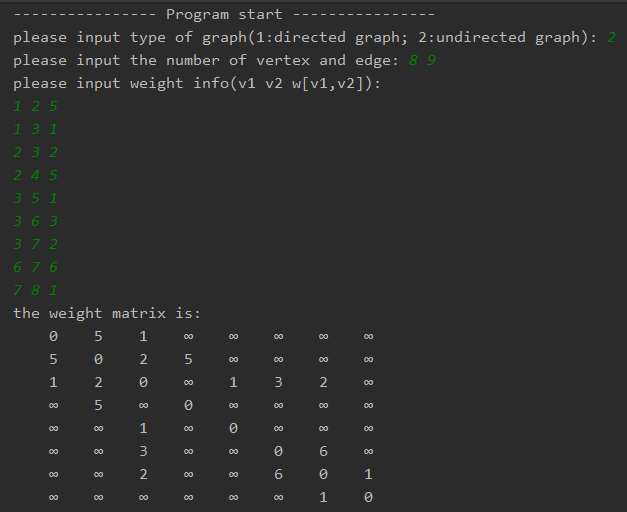
程序输出

（邻接矩阵，矩阵元素M[i][j]表示顶点Vi与Vj间的距离）

（各个顶点间的最短路径以及路径长度，对于此例，顶点V4与V6或V8间的距离都是10，是距离最远的两个顶点对）

（此图的直径）

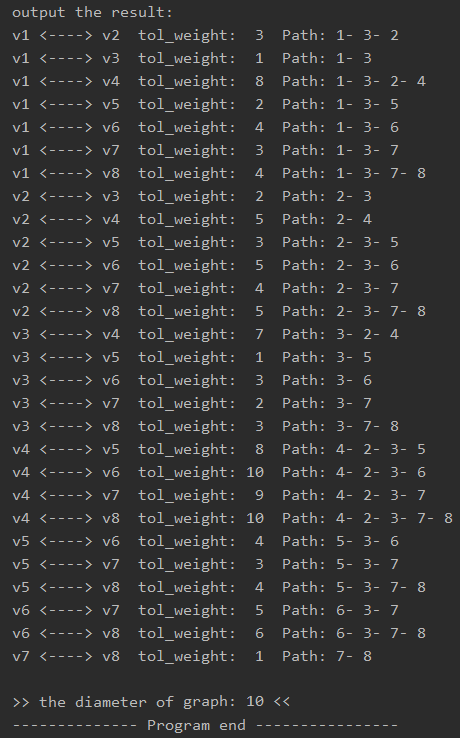
Python源代码

# ----------------------------------------------
# Project： calculate diameter of graph
# Using floyd algorithm
# ----------------------------------------------
# define function: print shortest path
def getPath(i, j):
    if i != j:
        if path[i][j] == -1:
            print('-', j+1, end='')
        else:
            getPath(i, path[i][j])
            getPath(path[i][j], j)
def printPath(i, j):
    print(' Path:', i+1, end='')
    getPath(i, j)
    print()
print('---------------- Program start ----------------')
# read data
flag = input('please input type of graph(1:directed '
             'graph; 2:undirected graph): ')
vertex, edge = input('please input the number of '
                     'vertex and edge: ').strip().split()
# initialized
flag = int(flag)
vertex = int(vertex)
edge = int(edge)
inf = 99999999
dis = []  # matrix of the shortest distance
path = []  # record the shortest path
for i in range(vertex):
    dis += [[]]
    for j in range(vertex):
        if i == j:
            dis[i].append(0)
        else:
            dis[i].append(inf)
for i in range(vertex):
    path += [[]]
    for j in range(vertex):
        path[i].append(-1)
# read weight information
print('please input weight info(v1 v2 w[v1,v2]): ')
for i in range(edge):
    u, v, w = input().strip().split()
    u, v, w = int(u)-1, int(v)-1, int(w)
    if flag == 1:
        dis[u][v] = w
    elif flag == 2:
        dis[u][v] = w
        dis[v][u] = w
print('the weight matrix is:')
for i in range(vertex):
    for j in range(vertex):
        if dis[i][j] != inf:
            print('%5d' % dis[i][j], end='')
        else:
            print('%5s' % '∞', end='')
    print()
# floyd algorithm
for k in range(vertex):
    for i in range(vertex):
        for j in range(vertex):
            if dis[i][j] > dis[i][k] + dis[k][j]:
                dis[i][j] = dis[i][k] + dis[k][j]
                path[i][j] = k
print('===========================================')
# output the result
print('output the result:')
if flag == 1:
    for i in range(vertex):
        for j in range(vertex):
            if (i != j) and (dis[i][j] != inf):
                print('v%d ----> v%d  tol_weight:'
                      '%3d' % (i+1, j+1, dis[i][j]))
                printPath(i, j)
            if (i != j) and (dis[i][j] == inf):
                print('v%d ----> v%d  tol_weight:'
                      '  ∞' % (i+1, j+1))
                printPath(i, j)
if flag == 2:
    for i in range(vertex):
        for j in range(i+1, vertex):
            print('v%d <----> v%d  tol_weight:'
                  '%3d' % (i+1, j+1, dis[i][j]), '', end='')
            printPath(i, j)
print()
for i in range(vertex):
    for j in range(vertex):
        if dis[i][j] == inf:
            dis[i][j] = 0
# max(max(dis)): the max item of two dimension matrix
print('>> the diameter of graph: %d <<' % max(max(dis)))
print('-------------- Program end ----------------')

---

Reference

最短路径_百度百科

最短路径—Dijkstra算法和Floyd算法

最短路径问题---Floyd算法详解 - CSDN博客

Floyd算法(记录路径) - CSDN博客