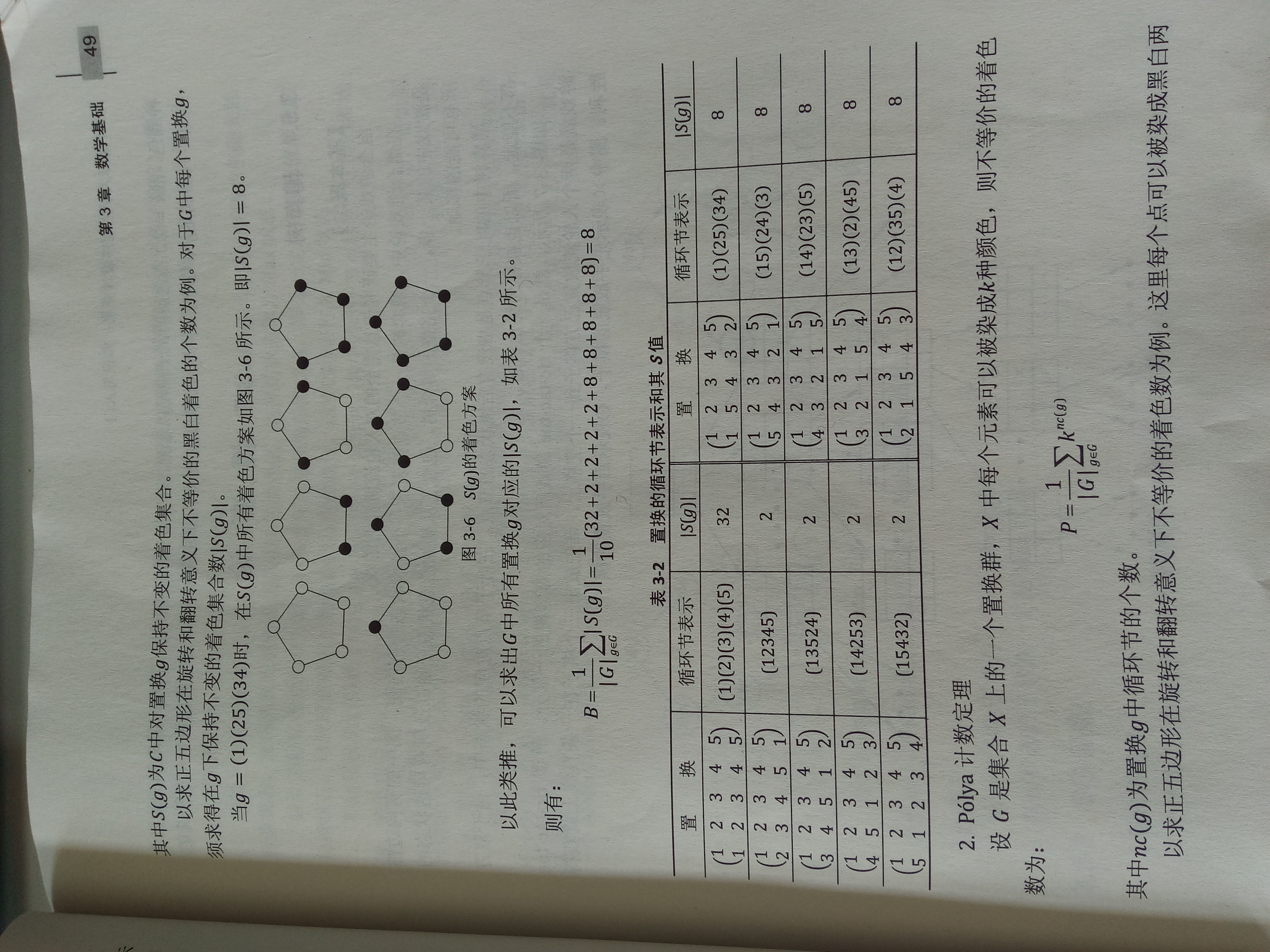
[ACM] POJ 2409 Let it Bead (Polya计数）

参考:https://blog.csdn.net/sr_19930829/article/details/38108871

 #include <iostream>
 #include <string.h>
 using namespace std;
 int c,n;//c种颜色，n个珠子
 int ans;

 int gcd(int a,int b)
 {
     return b==?a:gcd(b,a%b);
 }

 int power(int p,int n)//快速幂求公式里的k的nc(g)次方
 {
     int ans=;
     while(n)
     {
         if(n&)
             ans*=p;
         p*=p;
         n/=;
     }
     return ans;
 }

 int main()
 {
     while(cin>>c>>n&&(c||n))
     {
         ans=;
         for(int i=;i<=n;i++)
             ans+=power(c,gcd(n,i));//相当于求图3-1中左边的循环群染色数
         if(n&)//是奇数，有n个包含(n/2+1)个循环节的循环群
             ans+=n*power(c,n/+);
         else
             ans+=(power(c,n/+)+power(c,n/))*(n/);
         ans/=*n;//别忘了除以置换群的总个数
         cout<<ans<<endl;
     }
     return ;
 }