字符串相似度算法（编辑距离算法 Levenshtein Distance）（转）

在搞验证码识别的时候需要比较字符代码的相似度用到“编辑距离算法”，关于原理和C#实现做个记录。

据百度百科介绍：

编辑距离，又称Levenshtein距离（也叫做Edit Distance），是指两个字串之间，由一个转成另一个所需的最少编辑操作次数，如果它们的距离越大，说明它们越是不同。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。

　　例如将kitten一字转成sitting：

　　sitten （k→s）

　　sittin （e→i）

　　sitting （→g）

　　俄罗斯科学家Vladimir Levenshtein在1965年提出这个概念。因此也叫Levenshtein Distance。

例如

• 如果str1="ivan"，str2="ivan"，那么经过计算后等于 0。没有经过转换。相似度=1-0/Math.Max(str1.length,str2.length)=1
• 如果str1="ivan1"，str2="ivan2"，那么经过计算后等于1。str1的"1"转换"2"，转换了一个字符，所以距离是1，相似度=1-1/Math.Max(str1.length,str2.length)=0.8

应用

　　DNA分析

　　拼字检查

　　语音辨识

　　抄袭侦测

感谢大石头在评论中给出一个很好的关于此方法应用的连接 补充在此：

小规模的字符串近似搜索，需求类似于搜索引擎中输入关键字，出现类似的结果列表，文章连接:【算法】字符串近似搜索

算法过程

1. str1或str2的长度为0返回另一个字符串的长度。 if(str1.length==0) return str2.length; if(str2.length==0) return str1.length;
2. 初始化(n+1)*(m+1)的矩阵d，并让第一行和列的值从0开始增长。
3. 扫描两字符串（n*m级的），如果：str1[i] == str2[j]，用temp记录它，为0。否则temp记为1。然后在矩阵d[i,j]赋于d[i-1,j]+1 、d[i,j-1]+1、d[i-1,j-1]+temp三者的最小值。
4. 扫描完后，返回矩阵的最后一个值d[n][m]即是它们的距离。

计算相似度公式：1-它们的距离/两个字符串长度的最大值。

为了直观表现，我将两个字符串分别写到行和列中，实际计算中不需要。我们用字符串“ivan1”和“ivan2”举例来看看矩阵中值的状况：

1、第一行和第一列的值从0开始增长

		i	v	a	n	1
	0	1	2	3	4	5
i	1
v	2
a	3
n	4
2	5

2、i列值的产生 Matrix[i - 1, j] + 1 ; Matrix[i, j - 1] + 1   ;    Matrix[i - 1, j - 1] + t

		i	v	a	n	1
	0+t=0	1+1=2	2	3	4	5
i	1+1=2	取三者最小值=0
v	2	依次类推：1
a	3	2
n	4	3
2	5	4

3、V列值的产生

		i	v	a	n	1
	0	1	2
i	1	0	1
v	2	1	0
a	3	2	1
n	4	3	2
2	5	4	3

依次类推直到矩阵全部生成

		i	v	a	n	1
	0	1	2	3	4	5
i	1	0	1	2	3	4
v	2	1	0	1	2	3
a	3	2	1	0	1	2
n	4	3	2	1	0	1
2	5	4	3	2	1	1

最后得到它们的距离=1

相似度：1-1/Math.Max(“ivan1”.length,“ivan2”.length) =0.8

算法用C#实现

public class LevenshteinDistance
    {
        /// <summary>
        /// 取最小的一位数
        /// </summary>
        /// <param name="first"></param>
        /// <param name="second"></param>
        /// <param name="third"></param>
        /// <returns></returns>
        private int LowerOfThree(int first, int second, int third)
        {
            int min = Math.Min(first, second);
            return Math.Min(min, third);
        }
 
        private int Levenshtein_Distance(string str1, string str2)
        {
            int[,] Matrix;
            int n = str1.Length;
            int m = str2.Length;
 
            int temp = 0;
            char ch1;
            char ch2;
            int i = 0;
            int j = 0;
            if (n == 0)
            {
                return m;
            }
            if (m == 0)
            {
 
                return n;
            }
            Matrix = new int[n + 1, m + 1];
 
            for (i = 0; i <= n; i++)
            {
                //初始化第一列
                Matrix[i, 0] = i;
            }
 
            for (j = 0; j <= m; j++)
            {
                //初始化第一行
                Matrix[0, j] = j;
            }
 
            for (i = 1; i <= n; i++)
            {
                ch1 = str1[i - 1];
                for (j = 1; j <= m; j++)
                {
                    ch2 = str2[j - 1];
                    if (ch1.Equals(ch2))
                    {
                        temp = 0;
                    }
                    else
                    {
                        temp = 1;
                    }
                    Matrix[i, j] = LowerOfThree(Matrix[i - 1, j] + 1, Matrix[i, j - 1] + 1, Matrix[i - 1, j - 1] + temp);
                }
            }
 	   for (i = 0; i <= n; i++)
            {
                for (j = 0; j <= m; j++)
                {
                    Console.Write(" {0} ", Matrix[i, j]);
                }
                Console.WriteLine("");
            }
 
            return Matrix[n, m];
        }
 
        /// <summary>
        /// 计算字符串相似度
        /// </summary>
        /// <param name="str1"></param>
        /// <param name="str2"></param>
        /// <returns></returns>
        public decimal LevenshteinDistancePercent(string str1, string str2)
        {
            //int maxLenth = str1.Length > str2.Length ? str1.Length : str2.Length;
            int val = Levenshtein_Distance(str1, str2);
            return 1 - (decimal)val / Math.Max(str1.Length, str2.Length);
        }
    }

1	<strong>调用</strong>

static void Main(string[] args)
        {
            string str1 = "ivan1";
            string str2 = "ivan2";
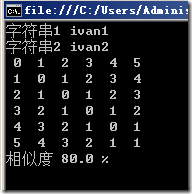
            Console.WriteLine("字符串1 {0}", str1);
 
            Console.WriteLine("字符串2 {0}", str2);
 
            Console.WriteLine("相似度 {0} %", new LevenshteinDistance().LevenshteinDistancePercent(str1, str2) * 100);
            Console.ReadLine();
        }

1	<strong>结果</strong>

http://www.cnblogs.com/ivanyb/archive/2011/11/25/2263356.html