BZOJ 后缀自动机四·重复旋律7

后缀自动机四·重复旋律7

时间限制:15000ms

单点时限:3000ms

内存限制:512MB

描述

小Hi平时的一大兴趣爱好就是演奏钢琴。我们知道一段音乐旋律可以被表示为一段数构成的数列。

神奇的是小Hi发现了一部名字叫《十进制进行曲大全》的作品集，顾名思义，这部作品集里有许多作品，但是所有的作品有一个共同特征：只用了十个音符，所有的音符都表示成0-9的数字。

现在小Hi想知道这部作品中所有不同的旋律的“和”（也就是把串看成数字，在十进制下的求和，允许有前导0）。答案有可能很大，我们需要对（10^9 + 7)取摸。

解题方法提示

输入

第一行，一个整数N，表示有N部作品。

接下来N行，每行包含一个由数字0-9构成的字符串S。

所有字符串长度和不超过 1000000。

输出

共一行，一个整数，表示答案 mod （10^9 + 7)。

样例输入

2
101
09

样例输出

131

小Hi：我们已经学习了后缀自动机，今天我们再来看这道有意思的题。

小Ho：好！这道题目让我们求的是若干的数字串所有不同子串的和。

小Hi：你能不能结合后缀自动机的性质来思考如何解决本题？

小Ho：这道题目既然是关于子串，那么我知道从后缀自动机的所有状态中包含的子串的集合恰好对应原串的所有不重复子串。

小Hi：很好。那你可以先简化问题，想想只有一个串怎么做？

小Ho：好的。这个难不倒我。我上次已经知道如何计算一个串所有不同子串的数量，现在这题也类似，只不过计算更加复杂一点。

小Hi：那你可以详细说说。

小Ho：我们举个例子，假设S="1122124"，其实就是我们熟悉的例子"aabbabd"啦。

状态	子串	endpos	sum
S	空串		0
1	1	{1,2,5}	1
2	11	{2}	11
3	112	{3}	112
4	1122,122,22	{4}	1266
5	2	{3,4,6}	2
6	11221,1221,221,21	{5}	12684
7	112212,12212,2212,212	{6}	126848
8	12	{3,6}	12
9	1122124,122124,22124,2124,124,24,4	{7}	1248648

小Ho：如果我们能像上面的表格一样求出每个状态中包含的子串的"和"，不妨记为sum(st)。那么我们只要求出Σsum(st)就是答案了。

小Hi：那你讲讲怎么求出每个状态的和？

小Ho：从初始状态开始一个个递推出来咯。比如我们现在要求状态6也就是{11221,1221,221,21}的和。我们知道到达状态6的边（transition）有2条，分别是trans[4][1]和trans[5][1]。如果我们已经求出sum(4) = 1266, sum(5)=2，那么我们就可以求出sum(6)=(sum(4) * 10 + 1 * |substrings(4)|]) + (sun(5) * 10 + 1 * |substring(5)|) = (12660 + 1 * 3) + (2 * 10 + 1 * 1) = 12684。

小Ho：换句话说，状态6里的{11221, 1221, 221}这三个子串是从状态4的所有（3个）子串乘以10再加1得到的；状态6里的{21}这个子串是从状态5的所有（1个）子串乘以10再加1得到的。也就是说对于状态st

sum(st) = Σ{sum(x) * 10 + c * |substrings(x)| | trans[x][c] = st}。

小Ho：我们知道SAM的状态和转移构成了一个有向无环图，我们只要求出状态的拓扑序，依次求出sum(st)即可。

小Hi：不错嘛。那我们回到原题的多个串的情况，怎么解决？

小Ho：多个串我就不会了 ┑(￣Д ￣)┍

小Hi：还记得我们第122周用后缀数组求多个串的最长公共字串时用到的技巧么？

小Ho：把多个串用'#'连接起来当作一个串来处理？

小Hi：没错。这次我们也使用这种方法，把所有串用冒号':' (':'的ACII码是58，也就是'0'的ASCII码+10，方便处理) 连接以来。以两个串"12"和"234"为例，"12:234"的SAM如图：

 '

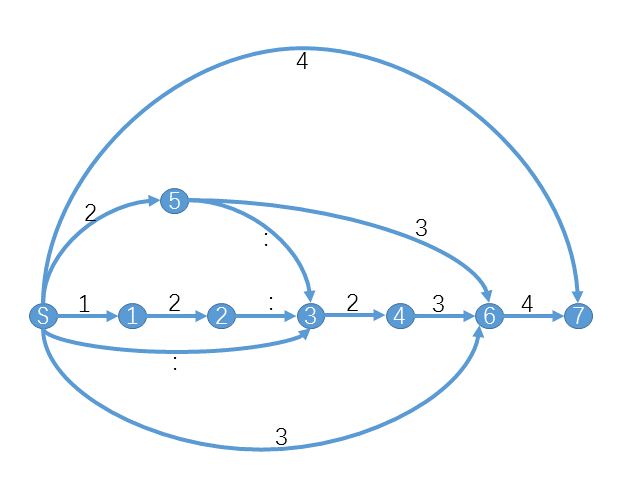状态	子串	endpos	｜valid-substrings｜	sum
S	空串		1	0
1	1	{1}	1	1
2	12	{2}	1	12
3	12:,2:,:	{3}	0	0
4	12:2,2:2,:2	{4}	0	0
5	2	{2,4}	1	2
6	12:23,2:23,:23,23,3	{5}	2	26
7	12:234,2:234,:234,234,34,4	{6}	3	272

小Ho：看上去如果我们把每个状态中带冒号的子串都排除掉，好像也是可以递推的！

小Hi：没错。如果我们用valid-substrings(st)表示一个状态中所有的不带冒号的子串，那么对于sum(st)我们有类似的递推式

sum(st) = Σ{sum(x) * 10 + c * |valid-substrings(x)| | trans[x][c] = st}

小Ho：那么关键就是|valid-substrings(st)|怎么求出来了？

小Hi：没错。|valid-substrings(st)|代表st中不带冒号的子串个数，这个值恰好就是从初始状态S到状态st的所有"不经过冒号转移的边"的路径数目。

小Ho：好像有点绕。

小Hi：举个例子，对于状态6，如果我们不经过标记为':'的转移，那么从S到状态6一共有2条路径，是S->6和S->5->6，分别对应不带冒号的子串3和23。前面已经提到过SAM的状态和转移构成了一个有向无环图，有向无环图上的路径数目也是一个经典的拓扑排序问题，可以参考之前我们的讨论

小Ho：我明白了。建完SAM之后对所有状态拓扑排序，然后按拓扑序递推一边求出|valid-substrings(st)|，一边求出sum(st)就可以了。好了，我写程序去了。

依然是HiHo怎么说，我们怎么做，2333~~~

 #include <bits/stdc++.h>

 #define fread_siz 1024

 inline int get_c(void)
 {
     static char buf[fread_siz];
     static char *head = buf + fread_siz;
     static char *tail = buf + fread_siz;

     if (head == tail)
         fread(head = buf, , fread_siz, stdin);

     return *head++;
 }

 inline int get_i(void)
 {
     register int ret = ;
     register int neg = false;
     register int bit = get_c();

     for (; bit < ; bit = get_c())
         if (bit == '-')neg ^= true;

     for (; bit > ; bit = get_c())
         ret = ret *  + bit - ;

     return neg ? -ret : ret;
 }

 inline int get_s(int *s)
 {
     register int ret = ;
     register int bit = get_c();

     while (bit < )
         bit = get_c();

     while (bit > )
         *(s + ret++) = bit - ,
         bit = get_c();

     return ret;
 }

 typedef long long lnt;

 const int maxn = ;
 const int mod  = ;

 /* AUTOMATON */

 int last = ;
 int tail = ;
 int fail[maxn];
 int step[maxn];
 int next[maxn][];

 inline void build(int *s)
 {
     while (~*s)
     {
         int c = *s++;
         int p = last;
         int t = tail++;
         step[t] = step[p] + ;
         while (p && !next[p][c])
             next[p][c] = t, p = fail[p];
         if (p)
         {
             int q = next[p][c];
             if (step[q] == step[p] + )
                 fail[t] = q;
             else
             {
                 int k = tail++;
                 fail[k] = fail[q];
                 fail[q] = fail[t] = k;
                 step[k] = step[p] + ;
                 for (int i = ; i < ; ++i)
                     next[k][i] = next[q][i];
                 while (p && next[p][c] == q)
                     next[p][c] = k, p = fail[p];
             }
         }
         else
             fail[t] = ;
         last = t;
     }
 }

 /* SOLVE PBM */

 lnt ans;
 lnt sum[maxn];
 lnt sub[maxn];
 int cnt[maxn];

 inline void solve(void)
 {
     static int que[maxn];
     static int inq[maxn];
     static int head, tail;

     head = , tail = ;
     que[tail++] = ;
     inq[] = ;

     while (head != tail)
     {
         int u = que[head++];
         for (int i = ; i < ; ++i)
             if (next[u][i])
             {
                 ++cnt[next[u][i]];
                 if (!inq[next[u][i]])
                     inq[que[tail++] = next[u][i]] = ;
             }
     }

     head = , tail = ;
     que[tail++] = ;
     sub[] = ;

     while (head != tail)
     {
         int u = que[head++], v;
         ans += sum[u];
         if (ans >= mod)
             ans %= mod;
         for (int i = ; i < ; ++i)
             if (v = next[u][i])
             {
                 sub[v] += sub[u];
                 sum[v] += sum[u] *  + i * sub[u];
                 if (sub[v] >= mod)
                     sub[v] %= mod;
                 if (sum[v] >= mod)
                     sum[v] %= mod;
                 if (--cnt[v] == )
                     que[tail++] = v;
             }
     }

     printf("%lld\n", ans);
 }

 /* MAIN FUNC */

 int s[maxn], len, n;

 signed main(void)
 {
     n = get_i();

     for (int i = ; i <= n; ++i)
     {
         len += get_s(s + len);
         s[len++] = ;
     }

     s[len] = -;

     build(s);

     solve();
 }

@Author: YouSiki