从头开始学JAVA[Day01]
1.Java程序的执行过程必须经过先编译,后解释两个步骤
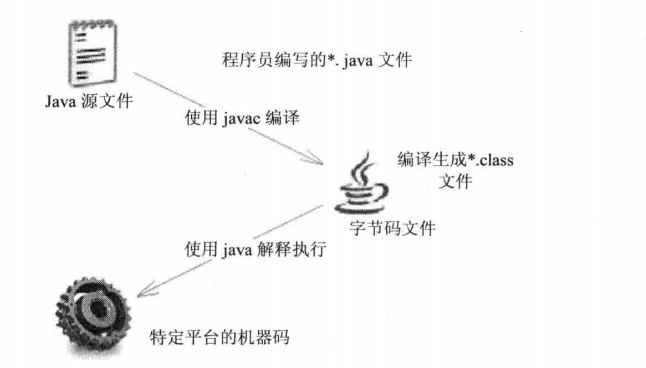
Jvm的统一标准,具体定义了JVM的如下细节:
--指令集
--寄存器
--类文件格式
--栈
--垃圾回收堆
--存储区
2.编译Java程序
javac -d destdir srcFile
destdir 存放路径地址
srcFile 源文件地址
3.运行Java程序
java Java类名
# 一个类中只能有一个public修饰的类
从头开始学JAVA[Day01]的更多相关文章
- 从头开始学Java【1】
1:常见的DOS命令 盘符的切换 d:回车 目录的进入 cd javase cd javase\day01\code 目录的回退 cd.. cd\ 清屏 cls 退出 exit 创建目录 md 删除目 ...
- 初学者学Java常遇到的问题,我都给你回答了!
前言 只有光头才能变强. 文本已收录至我的GitHub精选文章,欢迎Star:https://github.com/ZhongFuCheng3y/3y 春节在家刷知乎,看到了一个知乎的问题:<学 ...
- 小白学Java:RandomAccessFile
目录 小白学Java:RandomAccessFile 概述 继承与实现 构造器 模式设置 文件指针 操作数据 读取数据 read(byte b[])与read() 追加数据 插入数据 小白学Java ...
- 从零开始学 Java - Spring 集成 Memcached 缓存配置(二)
Memcached 客户端选择 上一篇文章 从零开始学 Java - Spring 集成 Memcached 缓存配置(一)中我们讲到这篇要谈客户端的选择,在 Java 中一般常用的有三个: Memc ...
- 从零开始学 Java - Spring 集成 ActiveMQ 配置(一)
你家小区下面有没有快递柜 近两年来,我们收取快递的方式好像变了,变得我们其实并不需要见到快递小哥也能拿到自己的快递了.对,我说的就是类似快递柜.菜鸟驿站这类的代收点的出现,把我们原来快递小哥必须拿着快 ...
- 从零开始学 Java - Spring 集成 Memcached 缓存配置(一)
硬盘和内存的作用是什么 硬盘的作用毫无疑问我们大家都清楚,不就是用来存储数据文件的么?如照片.视频.各种文档或等等,肯定也有你喜欢的某位岛国老师的动作片,这个时候无论我们电脑是否关机重启它们永远在那里 ...
- 从零开始学 Java - 我放弃了 .NET ?
这不是一篇引起战争的文章 毫无疑问,我之前是一名在微软温暖怀抱下干了近三年的 .NET 开发者,为什么要牛(sha)X一样去搞 Java 呢?因为我喜欢 iOS 阿!哈哈,开个玩笑.其实,开始学 Ja ...
- 从零开始学 Java - Spring 集成 ActiveMQ 配置(二)
从上一篇开始说起 上一篇从零开始学 Java - Spring 集成 ActiveMQ 配置(一)文章中讲了我关于消息队列的思考过程,现在这一篇会讲到 ActivMQ 与 Spring 框架的整合配置 ...
- 从零开始学 Java - 利用 Nginx 负载均衡实现 Web 服务器更新不影响访问
还记得那些美妙的夜晚吗 你洗洗打算看一个小电影就睡了,这个时候突然想起来今天晚上是服务器更新的日子,你要在凌晨时分去把最新的代码更新到服务器,以保证明天大家一觉醒来打开网站,发现昨天的 Bug 都不见 ...
随机推荐
- JVM进程占用CPU过高问题排查
上午收到报警,某台机器上的CPU负载过高,通过逐步的排查,解决了问题,下面记录一下整个排查的过程. 首先,登录上对应的机器,通过top命令找到占用CPU过高的进程ID,也就是PID,为29126, 然 ...
- h5手机查看
1.装个node:2.全局装个anywhere的npm包.(npm i -g anywhere)3.大功告成,现在到任意目录下用命令行执行anywhere就可以:(-p 参数可以设置启动端口) 补充: ...
- 015模块——起别名
1.import起别名:通过as关键字可以给模块起别名: 模块名一旦起别名,原模块名就不能再使用 2.起别名的作用:①可以简化模块名字 import mmmmmmmmmmm3 as my_m3 pri ...
- codeforces342B
Xenia and Spies CodeForces - 342B Xenia the vigorous detective faced n (n ≥ 2) foreign spies lined u ...
- poj-1904(强连通缩点)
题意:有n个王子,每个王子都有k个喜欢的女生,王子挑选喜欢的女生匹配,然后再给你n个王子最开始就定好的匹配,每个王子输出能够结合且不影响其他王子的女生匹配 解题思路:强连通缩点,每个王子与其喜欢的女生 ...
- C#语法相比其它语言比较独特的地方
C#语法相比其它语言比较独特的地方(一) 本文讲解了switch语句可以用来测试string型的对象.多维数组.foreach语句.索引器和Property等内容 1,switch语句可以用来测试st ...
- nginx 详细配置
Nginx全局变量 Nginx中有很多的全局变量,可以通过$变量名来使用.下面列举一些常用的全局变量: 变量 说明 boxClass 需要执行动画的元素的 变量 说明 $args 请求中的参数,如ww ...
- time、datetime、calendar
time 1. Python中表示时间的方式 l 时间戳 l 格式化的时间字符串 l 元组(struct_time)共九个元素.由于Python的time模块实现主要调用C库,所以各个平台可能 ...
- [JSOI2009]密码 [AC自动机]
题面 bzoj luogu 首先看到这题就知道随便暴枚 只要是多项式算法都能过 先常规建AC自动机 注意被别的单词包含的单词没有存在的价值 剩余单词状压 大力dp f[长度][节点编号][状态] \( ...
- [PRIMITIVE TECHNOLOGY]澳洲小哥的黑皮豆/black been/摩顿湾板栗(栗子)/Moreton Bay Chestnut
wiki:https://en.wikipedia.org/wiki/Castanospermum inner:http://blog.sciencenet.cn/blog-309517-770951 ...
