倍增法求LCA（最近公共最先）

对于有根树T的两个结点u、v，最近公共祖先x=LCA(u,v)表示一个结点x，满足x是u、v的祖先且x的深度尽可能大。

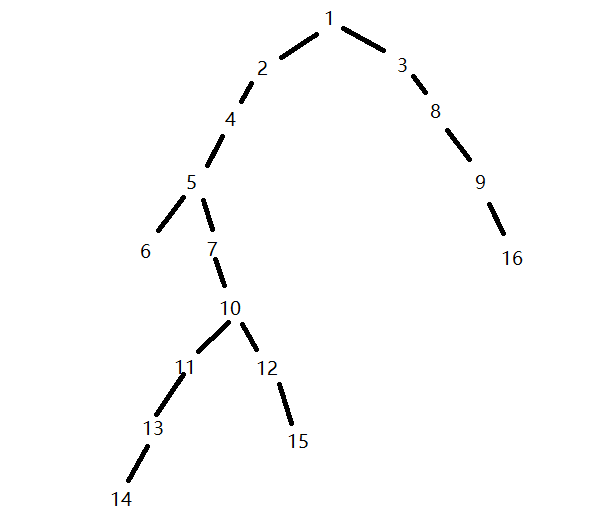
如图，根据定义可以看出14和15的最近公共祖先是10,   15和16的最近公共祖先是1,     6和5的最近公共祖先是5......

假如我要求14和16的最近公共祖先，要怎么做呢？

最暴力的做法，就是先看14和16在不在同一层，如果他们不在同一层，那么较深的那个点往上爬（即距离根较远的那个点）

一直爬，爬到两点的深度一样

当两点深度一样时，判断他们是否在同一个点上，如果不是，则两个点同时往上爬，直到这两个点是同一个点

显然，这么做一般来说都是不行的。

下面介绍倍增法（图是用vector存的）

既然一步一步往上爬太慢了，那就一次爬远一点

我们预处理一个数组fa【x】【i】使游标快速移动，大幅度减少跳转次数。

fa【x】【i】表示 点x的第2^i个祖先

拿上图来说，fa【15】【0】就是点15的第2^0个祖先，即12（fa【15】【0】=12）

　　　　　　fa【15】【1】就是点15的第2^1个祖先，即10（fa【15】【1】=10）

　　　　　　　  fa【15】【2】就是点15的第2^2个祖先，即5（fa【15】【2】=5）

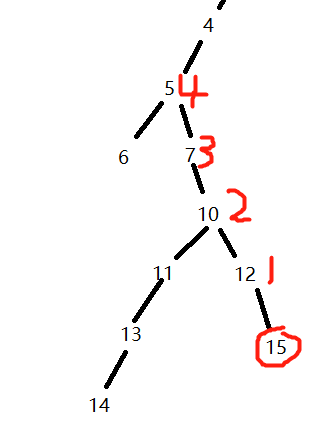
怎么预处理出这个数组呢？我们观察上图，15的第一个祖先是12，12的第一个祖先是10

即fa【15】【0】=12     fa【12】【0】=10

而15的第二个祖先是10，和12的第一个祖先是一样的

fa【15】【1】=10

也就是说，对于点15来说，15的第二个祖先就是15的第一个祖先的第一个祖先（点12的第一个祖先）

用数组表示是fa[15][1]=fa[ fa[15][0] ][ 0 ];

即fa[15][1]=fa[12][0]

推广到第2^i个祖先：递推式：fa[rt][i]=fa[fa[rt][i-1]][i-1];（rt为当前节点）

预处理代码：（depth数组存的是当前节点的深度）

void dfs(int f,int rt )//rt是当前节点，f是当前节点的父亲
{
    depth[rt]=depth[f]+;
    fa[rt][]=f;
    for(int i=;i<;++i)//自己估计i的范围
    fa[rt][i]=fa[fa[rt][i-]][i-];
    for(int i=;i<E[rt].size();++i)//用vector存的图，遍历当前节点的每一个孩子
    dfs(rt,E[rt][i]);
}

下一个问题是，游标移动到哪里合适？

我们的原则是，先让两个点的深度一致

然后，让两个点同时跳相同的步数

1.如果跳出根以外了，就不跳

2.如果跳到的点是相同的点，也不跳（不一定是最近的公共祖先）

不是以上两种情况，就跳

举个栗子，如图：

假如我们问14和15的lca是哪个点

按照规则

我们先让14和15在同一层上（深度一致）

14跳到了13

然后，我们看跳多少步合适，如果i=3，即2^3=8步，发现已经跳出根以外了，不跳

再看i=2, 2^2=4，13和15的第四个祖先都是5，不跳

再看i=1，即跳2步，发现都是10，不跳

再看i=0，跳一步，13跳一步到11,15跳一步到12，两个点不相同，可以跳

此时第一遍循环结束，判断这两个点的第一个祖先是不是同一个点

如果是，则找到了

如果不是，那就继续进行循环

用图表示：

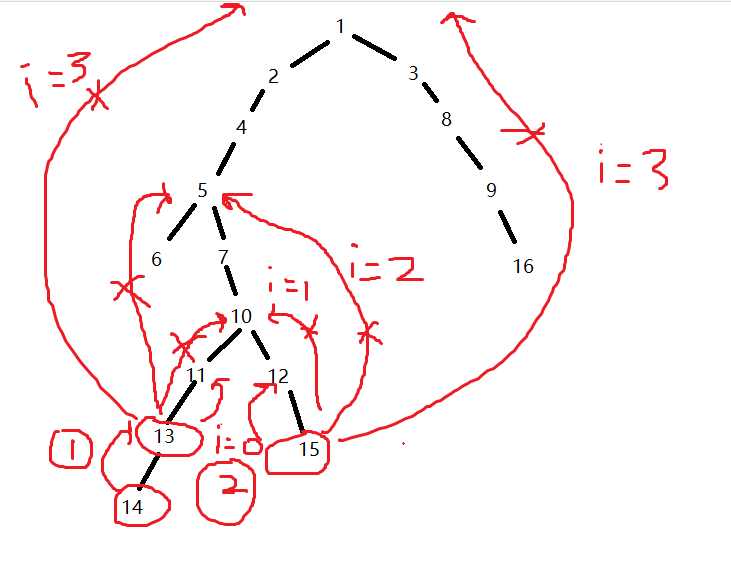
第一步是14跳到13

第二步是13跳到11,15跳到12

发现11和12的第一个祖先都是10，找到答案，结束循环 （时间是log级别的）

代码：

int lca(int x,int y)//找x和y的最近公共祖先
{
    if(depth[x]<depth[y])//调整x的深度大一些
        swap(x,y);
    while(depth[x]!=depth[y])//使x和y的深度一致
    {
        for(int i=;i>=;--i){//初始常数自己根据问题进行调整
            if(depth[x]-(<<i)>=depth[y])
                x=fa[x][i];
        }
    }
    if(x==y) return x;
    while(fa[x][]!=fa[y][])//当x和y的第一位祖先都一样时退出循环
    {
        for(int i=;i>=;--i){
        //如果没有出界而且两点的祖先不一样，就跳
                if(fa[x][i]!=&&fa[x][i]!=fa[y][i])
            x=fa[x][i],y=fa[y][i];
        }
    }
    return fa[x][];
}        

代码自己写的，有点丑，网上的没看懂....

下面给出测试代码和样例，大家可以去试一试，样例就是第一幅图

#include <iostream>
#include <queue>
#include <vector>
#include <stdio.h>
using namespace std;
vector<int> E[];
int depth[];
int fa[][];
void dfs(int f,int rt )
{
    depth[rt]=depth[f]+;
    fa[rt][]=f;
    for(int i=;i<;++i)
    fa[rt][i]=fa[fa[rt][i-]][i-];
    for(int i=;i<E[rt].size();++i)
    dfs(rt,E[rt][i]);
}
int lca(int x,int y)
{
    if(depth[x]<depth[y])//调整左边深
        swap(x,y);
    while(depth[x]!=depth[y])
    {
        for(int i=;i>=;--i){
            if(depth[x]-(<<i)>=depth[y])
                x=fa[x][i];
        }
    }
    if(x==y) return x;
    while(fa[x][]!=fa[y][])
    {
        for(int i=;i>=;--i){
            if(fa[x][i]!=&&fa[x][i]!=fa[y][i])
            x=fa[x][i],y=fa[y][i];
        }
    }
    return fa[x][];
}
int main()
{
    int l,r;
    for(int i=;i<=;++i){
        cin>>l>>r;
        E[l].push_back(r);
    }
    dfs(,);
    int a,b,t=;
    while(t--)
    {
        cin>>a>>b;
        cout<<lca(a,b)<<endl;
    }

    return ;
}
/*
输入图：
1 2
2 4
4 5
5 6
5 7
7 10
10 11
10 12
11 13
12 15
13 14
1 3
3 8
8 9
9 16
*/