2016第七届蓝桥杯C/C++语言A组

一：问题：

某君新认识一网友。
当问及年龄时，他的网友说：
“我的年龄是个2位数，我比儿子大27岁,
如果把我的年龄的两位数字交换位置，刚好就是我儿子的年龄”

请你计算：网友的年龄一共有多少种可能情况？

提示：30岁就是其中一种可能哦.

请填写表示可能情况的种数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

答案：这题似乎只要列一下方程组就可以得出答案7了吧。

二：题目：

某君从某年开始每年都举办一次生日party，并且每次都要吹熄与年龄相同根数的蜡烛。

现在算起来，他一共吹熄了236根蜡烛。

请问，他从多少岁开始过生日party的？

请填写他开始过生日party的年龄数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

答案：

标准的递增数列求和

#include<stdio.h>
int main()
{
    int a, b;
    for (a = ; a < ; a++)
    {
        int c = ;
        for (b = ; b < ; b++)
        {
            c = c + a + b;
            if (c == )
            {
                printf("        %d %d\n", a, b);
                break;
            }
        }
        printf("%d\n", a);
    }
    return ;
}

三：题目：

方格填数

如下的10个格子
填入0~9的数字。要求：连续的两个数字不能相邻。

（左右、上下、对角都算相邻）

一共有多少种可能的填数方案？

请填写表示方案数目的整数。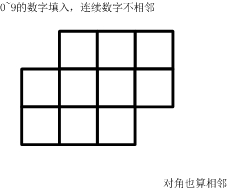
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

答案：

八：题目：

四平方和

四平方和定理，又称为拉格朗日定理：
每个正整数都可以表示为至多4个正整数的平方和。
如果把0包括进去，就正好可以表示为4个数的平方和。

比如：
5 = 0^2 + 0^2 + 1^2 + 2^2
7 = 1^2 + 1^2 + 1^2 + 2^2
（^符号表示乘方的意思）

对于一个给定的正整数，可能存在多种平方和的表示法。
要求你对4个数排序：
0 <= a <= b <= c <= d
并对所有的可能表示法按 a,b,c,d 为联合主键升序排列，最后输出第一个表示法

程序输入为一个正整数N (N<5000000)
要求输出4个非负整数，按从小到大排序，中间用空格分开

例如，输入：
5
则程序应该输出：
0 0 1 2

再例如，输入：
12
则程序应该输出：
0 2 2 2

再例如，输入：
773535
则程序应该输出：
1 1 267 838

资源约定：
峰值内存消耗 < 256M
CPU消耗 < 3000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

答案：

蓝桥杯果然暴力出真理

#include <iostream>
#include <cmath>
#include <stdio.h>
#include <cstdio>
#include <cstring>
#include<algorithm>
#include<time.h>
#include<math.h>
#include <stdlib.h>
#include <string.h>
#include <stack>  
 
using namespace std;
 
int a[], temp;
int handle(int temp)
{
    for (a[] = ; a[] < ; a[]++)
        for (a[] = a[]; a[] < ; a[]++)
            for (a[] = a[]; a[] < ; a[]++)
            {
                a[] = (int)sqrt(temp - (a[] * a[] + a[] * a[] + a[] * a[]));
                if (a[] * a[] + a[] * a[] + a[] * a[] + a[] * a[] == temp)
                {
                    sort(a, a + , less<int>());
                    return ;
                }
            }
    return ;
}
 
int main()
{
    while ()
    {
        scanf("%d", &temp);
        if (handle(temp))
        {
            printf("%d %d %d %d\n", a[],a[],a[],a[]);
        }
        else
        {
            printf("inexistence\n");
        }
    }
    return ;
}

九：题目：

密码脱落

X星球的考古学家发现了一批古代留下来的密码。
这些密码是由A、B、C、D 四种植物的种子串成的序列。
仔细分析发现，这些密码串当初应该是前后对称的（也就是我们说的镜像串）。
由于年代久远，其中许多种子脱落了，因而可能会失去镜像的特征。

你的任务是：
给定一个现在看到的密码串，计算一下从当初的状态，它要至少脱落多少个种子，才可能会变成现在的样子。

输入一行，表示现在看到的密码串（长度不大于1000）
要求输出一个正整数，表示至少脱落了多少个种子。

例如，输入：
ABCBA
则程序应该输出：
0

再例如，输入：
ABDCDCBABC
则程序应该输出：
3

资源约定：
峰值内存消耗 < 256M
CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

答案：

计算原字符串与逆序字符串的LCS（最长公共子序列）的长度，用字符串长度减去LCS的长度就是最小回文代价

#include <iostream>
#include <cmath>
#include <stdio.h>
#include <cstdio>
#include <cstring>
#include<algorithm>
#include<time.h>
#include<math.h>
#include <stdlib.h>
#include <string.h>
#include <stack>  
 
using namespace std;
 
int f[][];
int len1, len2;
int LCS(char a[], char b[])
{
    int i, j;
        len2=len1 = strlen(a);
        for (i = ; i <= len1; i++)
        {
            f[i][] = ;
        }
        for (i = ; i <= len2; i++)
        {
            f[][i] = ;
        }
        for (i = ; i <= len1; i++)
        {
            for (j = ; j <= len2; j++)
            {
                if (a[i - ] == b[j - ])
                {
                    f[i][j] = f[i - ][j - ] + ;
                }
                else
                {
                    f[i][j] = f[i - ][j]>f[i][j - ] ? f[i - ][j] : f[i][j - ];
                }
            }
        }
    return ;
}
 
int main()
{
    int len;
    int j = ,i=;
    char a[], b[  ];
    scanf("%s", &a);
    len = strlen(a);
    for ( i = len-; i >= ; i--)
    {
        b[j] = a[i];
        j++;
        printf("%c", a[i]);
    }
    LCS(a, b);
    printf("\n%d\n", len-f[len1][len2]);
    return ;
}

十：题目：

最大比例

X星球的某个大奖赛设了M级奖励。每个级别的奖金是一个正整数。
并且，相邻的两个级别间的比例是个固定值。
也就是说：所有级别的奖金数构成了一个等比数列。比如：
16,24,36,54
其等比值为：3/2

现在，我们随机调查了一些获奖者的奖金数。
请你据此推算可能的最大的等比值。

输入格式：
第一行为数字 N (0<N<100)，表示接下的一行包含N个正整数
第二行N个正整数Xi(Xi<1 000 000 000 000)，用空格分开。每个整数表示调查到的某人的奖金数额

要求输出：
一个形如A/B的分数，要求A、B互质。表示可能的最大比例系数

测试数据保证了输入格式正确，并且最大比例是存在的。

例如，输入：
3
1250 200 32

程序应该输出：
25/4

再例如，输入：
4
3125 32 32 200

程序应该输出：
5/2

再例如，输入：
3
549755813888 524288 2

程序应该输出：
4/1

资源约定：
峰值内存消耗 < 256M
CPU消耗 < 3000ms

答案：

先对各项排序，两两相除并约分，只要保证每次计算结果大于1，最后剩下的就是最大公比。

　　需要注意去重，以及公比为1的情况。

#include <iostream>
#include <cmath>
#include <stdio.h>
#include <cstdio>
#include <cstring>
#include<algorithm>
#include<time.h>
#include<math.h>
#include <stdlib.h>
#include <string.h>
#include <stack>  
 
using namespace std;
 
struct fraction
{
    _int64 son, mom;
}adata[];
 
__int64 GCD(__int64 a, __int64 b)
{
    __int64 c;
    while (c = a%b)
        a = b, b = c;
    return b;
}
 
fraction getfra(fraction a, fraction b)
{
    if (a.son == b.son&&a.mom==b.mom)
    {
        return a;
    }
    _int64 gcd;
    gcd = GCD(a.mom, b.mom);
    a.mom /= gcd;
    b.mom /= gcd;
    gcd = GCD(a.son, b.son);
    a.son /= gcd;
    b.son /= gcd;
    a.son *= b.mom;
    b.son *= a.mom;
    if (a.son < b.son)
    {
        a.mom = a.son;
        a.son = b.son;
    }
    else
        a.mom = b.son;
    return a;
}
 
int main()
{
    int i, j, n;
    _int64 temp[];
    scanf("%d", &n);
    for (i = ; i < n; i++)
    {
        scanf("%lld", &temp[i]);
        adata[i].mom = ;
    }
    sort(temp, temp + n);
    for (i=j = ; i < n; i++)
    {
        if (temp[i] != temp[i + ])
            adata[j++].son = temp[i];
    }
    for (i = j - ; i; i--)
    {
        for (n = ; n < i; n++)
        {
            adata[n]=getfra(adata[n], adata[n + ]);
        }
    }
    if (j == )
        printf("1/1");
    else
        printf("%lld/%lld", adata[].son, adata[].mom);
    return ;
}