The Separator in Grid_BFS

Description

Given a connected, undirected graph G = (V, E), where V is the vertex set consisting a collection of nodes, and E is the set of edges, each of which connects two nodes from V. A vertex subset S is a separator if the subgraph induced by the vertices in V, but not in S, has two connected components. We shall use the notation [S, W, B] to represent the partition, where the removal of the separator S will give two connected components W and B.

In this problem, we consider the separators in grids. Each node in a grid is connected to its eight neighbors (if they exist). In Figure-1, we illustrate a partition of a 6*6 grid with a 9-point separator (gray nodes in the figure). The nodes on the left of the separator are in set W (white nodes), and the nodes on the right of the separator are in set B (black nodes).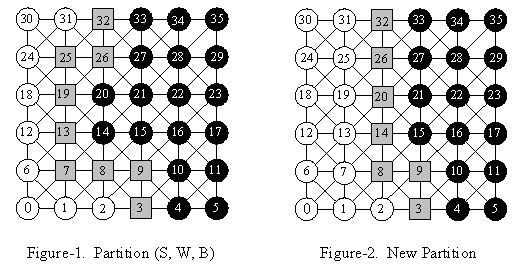 

To simplify the problem, you can assume that all the separators referred in this problem satisfy the following restrictions: 
1) It’s a minimal separator. A separator is minimal if no subset of it forms a separator. 
2) It begins from a node on the top line of the grid, except the corner (i.e. 30 and 35 in the figures), and ends with a node on the bottom line of the grid, also except the corner (i.e. 0 and 5 in the figures). 
3) On its way from top to bottom, it can go left, right or down, but never go up.

Now we describe a method to improve a given partition on a grid, through which we can reduce the number of nodes in the separator. This method contains two steps: 
1) Select several nodes from B and add them into S. Any of the selected nodes must have a left neighbor which is in S. 
2) Remove several nodes from S (excluding the nodes added in the former step), and add them into W.

After the improvement, we should ensure S is still a separator, and make the number of nodes in S as small as possible. As for Figure-1, we should add 14 and 20 into S, and remove 7, 13, 19 and 25 from S. After that, we obtain a new partition with a 7-point separator shown in Figure-2.

Your task is, given a partition on a grid, to determine the least number of nodes in the separator after the improvement.

Input

There are several test cases. Each case begins with a line containing two integers, N and M (3 <= M, N <= 200). In each of the following N lines, there are M characters, describing the initial partition of the M*N grid. Every character is 'S', 'W' or 'B'. It is confirmed that each of these three characters appears at least once in each line, and 'W's are always on the left of 'S's.

A test case of N = 0 and M = 0 indicates the end of input, and should not be processed.

Output

For each test case, you should output one line containing one integer, which is the least number of nodes in the separator after the improvement.

Sample Input

6 6
WWSBBB
WSSBBB
WSBBBB
WSBBBB
WSSSBB
WWWSBB
0 0

Sample Output

7

【题意】给出一个n*m的矩阵，包含w,s,b，s是分界线，每行每种都至少有一个，B在他的左边是S时能变成S，S无条件可以变成w,求最少的分界线s

【思路】先把能变成S的B全部变成s，然后进行BFS从第一行的S开始，把（0，s）（0，s+1）入队，进行三个方向的搜索下、左、右

#include<iostream>
#include<stdio.h>
#include<queue>
#include<string.h>
using namespace std;
const int inf=0x7777777;
const int N=;
int n,m,ans,s;
char mp[N][N];
int vis[N][N];
int di[][]={,,,,,-};//以左上角为原点，下，右，左开始搜索
struct node
{
    int x,y;
    int step;
};
bool go(int x,int y)
{
    if(x<||x>n-||y<||y>m-) return false;
    else return true;
}
void bfs()
{
    memset(vis,,sizeof(vis));
    queue<node>qu;
    node pre,next;
    pre.x=,pre.y=s;
    pre.step=;
    qu.push(pre);
    vis[][s]=;
    if(s+<m-)
    {
        pre.x=;pre.y=s+;
        pre.step=;
        qu.push(pre);
        vis[][s+]=;
    }
    while(!qu.empty())
    {
        pre=qu.front();
        qu.pop();
        if(pre.x==n-&&pre.y>&&pre.y<m-)
        {
            ans=min(ans,pre.step);
        }
        for(int i=;i<;i++)
        {
            int xx=pre.x+di[i][];
            int yy=pre.y+di[i][];
            if(go(xx,yy)&&(!vis[xx][yy])&&mp[xx][yy]=='S')
            {
                next.x=xx;
                next.y=yy;
                next.step=pre.step+;
                vis[xx][yy]=;
                qu.push(next);
            }
        }
    }
}
int main()
{
    while(~scanf("%d%d",&n,&m),n||m)
    {
        for(int i=;i<n;i++)
        {
             scanf("%s",mp[i]);
             int flag=;
             for(int j=;j<m;j++)
             {
                 if(mp[i][j]=='B'&&mp[i][j-]=='S'&&!flag)
                 {
                     mp[i][j]='S';
                     flag=;
                 }
             }
        }
        for(int i=;i<m;i++)
        {
            if(mp[][i]=='S')
            {
                s=i;
                break;
            }
        }
        ans=inf;
        bfs();
        printf("%d\n",ans);

    }
    return ;
}