Sklearn库例子2:分类——线性回归分类(Line Regression )例子
线性回归:通过拟合线性模型的回归系数W =(w_1,…,w_p)来减少数据中观察到的结果和实际结果之间的残差平方和,并通过线性逼近进行预测。
从数学上讲,它解决了下面这个形式的问题: 
LinearRegression()模型在Sklearn.linear_model下,他主要是通过fit(x,y)的方法来训练模型,其中x为数据的属性,y为所属类型。线性模型的回归系数W会保存在他的coef_方法中。
例如:
>>> from sklearn import linear_model
>>> clf = linear_model.LinearRegression()
>>> clf.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
>>> clf.coef_
array([ 0.5, 0.5])
实例:
使用的数据集为Sklearn.dataset.load_diabetes()一个关于糖尿病的数据集。
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAx0AAAEWCAIAAACMo20uAAAgAElEQVR4nO3dz2rrxvvH8d+NGINXvZOAjbPpdQQORxjau8giEDvQTVff7fkuDpw46aJ3kFKyCIm+dNtVdoXCQb+F/j0zekYaWY/8L+8XoqSKPBqNJetzZsbK/2UAAACw8H+HrgAAAMCZIFcBAADYIFcBAADYIFcBAADYIFcBAADYIFcBAADYIFcBAADYIFcBAADYIFcBAADYIFcBAADYIFcBAADYIFcBAADYIFf1k6bpCRU7noNU2HynJ9fsAIAjZ5Kr0vViNt9Y36IeVpPpantEZY5zmE6xj8l0ljxYlFof6WMyvVy31brvTkdoh+73xXynHQVuE6M3wljnu2n+QgBAD+SqeCeaqzqRqxq/21xOkke7fR2H9G6+uCNZAcCoxs5V6Xoxm0xnk+lsIj/T07v5tFzv3NQfk2Ll5XoTuNfqr31Mppfrh+pX8p/mnWWm60X+q+qFzWqLNcmjn0XqWOAV1VKrRvtUxW7U7QMt6VCPVHRUBJtO7lS2T2c7BCuWbi4nwaNufV+USjZ2Gjh/AjuNOQqvYlUjxJwbLYcT+3K15tpK2e2kFtV2ym2TMf5hAACojZqr0vWivm9tk+rT3wkl22QmbkJOz42WgUKvdbYX+4opM10v5J3JOZx0cxkqKpCrvJucWqtQ68UchaxSTDnVnTiq6dLNpfZ2hNohsI3sf9L7olpqG3VuKNvoO405CrdmTmdV5LnxmEzL9UXmU8+HPs2lH071brZdXMFT7mEVDuUAAANj5qr0bu7cUAPjTeqNpPm/Kud+owWdqDLd+vvbpOtF3WsSk6tEU4Q2C+097ijqKqlN0WwZrcco1HTV/8a0Q2ibzvcu8r0ONqy2jVpI1Lspeevjzg03r4Syab/m0tukfDeDF1f7KccsKwAY15i5yv/HsZI5ymGO1bbZDePfOST/taHbSVyZTkwRgy/1Mt+k8blKySj+ZqHWCx+FXiVRSvBIvVup2nT+qNl8k8a0Q/s2jUHemNqGKtk8x/RtwiODLe9m5hUr6hx1bvjzsQLnQ8/mUleWb1bw4mo/5bREDgCwc5BcVdwRvT6PuAykv9Y4V+ljJQfNVV3DNxG5qqXpArmqqx06K7ZN9ClWrbVVK9kcNwz1mTk7jXs3JaU1Os+NHrmqf3O5Kw1yFVOsAGA8hxgH9G4JvcbsQq8dPA7YlX6yA+aqnkOi3v8G7sS9xwG1Ckd961A7PUK1DVbS3am+jbbTqHdTauuvahuvDI8DRpxanRWTsWnIOCD9VQAwrkPMW5ef9cUk3+ZU3MAc8+BrWyeSt5fp32zcucYPK1k9OV/b/ULcmLkqWCW/HO1IRa4KN11osnxUOzS38fcVXdvWc0MJc3IbfacxRxF6O7Kdzg3ZnnEvV2uuH07UvHXmVwHAoZjlKn/iSOuX8Muhjfz2I+8E1fbB5ywEXttyO+kss/mPeHlEje+9O2lgNim+1r5zrpLFxhyFMqzWqLb+nIVw04lv5jdGl7raQd9G7CvUQaK/L6FzQ+40tE1gpzFH4b4d7vcBY84N/zkLIpvGvFytubYy5jkL4VNO9KvxzAUAGAN/xwbwDO7UOdbHGZClAGBs5CrA1/t5687I7LHODed56wAwPnIV0NR7frd8hsIxhipmVgHAXpCrAAAAbJCrAAAAbJCrAAAAbJCrAAAAbBjkqjfgxA2/CgAAyExy1fs//7KwnPQy/CoAACAjV7GwvJOrAABGyFUsLOQqAIANchULC7kKAGCDXMXCQq4CANggV7GwkKsAADbIVf++//Pv0/OLyTYsJ7oMvwoAAMjGy1VfPs2qP0M7+fRttDvit6vp8vp5SAkv1/PZxc3L4G2G10Qsz7cXamn++m9XVSNPky9jNfL5L8OvAgAAspFy1ZdPMku9XM/Hi1ZnmaterueziVKat/7b1bSu1dPNkmi18zL8KgAAIBsnVzUSxtekvuU/317UXSyzq6/VyuX1TVL3b31N3L6ub1fT5fXX6rVVgJD7ymPHbDKdTea3T+Xen26W5e5CSUXuqFlIYxv1EOxy1dPN8uJT0uyv8tfLVjWtwAdchl8FAABk4+Sqlg6qb1d1EMnHCpMv/5RJJX9JnqjqBJNnhXzAq4gRom+mChNOl9LTzbJIRTJ8+EGkrm35QqfmXz450arcJnAIVrHm+fZifvvUHAcMrZcbkKt2XYZfBQAAZKPNrxLzfkTXkb9UQef59sLp+Gn+7KQZd/3y+rmZmV6u57Orr6EsJReRmZ5vL/weoHwv4XHAunyTXPVyPV9ePzdDUmi9cxRjzmM782X4VQAAQDb+9wHLgOXc8huzrZ24IANKIz+JGHFx81KtF4N99XJx8yJH8UQsk4vITF8TNwVWv2rmquaEcYNc9XSzFAmvLi20XtaTUDVkGX4VAACQ7ek5C/5wnsgxhrmqpWOs/n6iHkr65KrAIQzPVflIn99i4fX1ms459Swdy/CrAACAbJRcpQy9lfHICy79clWvcUB1UYfzeo4Dhg5hcK5Su9yuvgbXl3tnTpXBMvwqAAAgG3Heuv+NvOTLP+oXA5vThoK5qnqtmFHuzFuvd1oFDn+Prf1VMfPWQ4ew/+dXMVHdbhl+FQAAkO3puaAiY4n1yZcqNkX2V31KGgUGnrMgAoesiTrFqugQCj5nwd9GP4S956q2fiyWnsvwqwAAgOx0/o6NNw7IwmK5DL8KAADIyFUsLO/kKgCAEXIVCwu5CgBg41RyFQvLiMvwqwAAgIxcxcLyTq4CABghV7GwkKsAADbIVSws5CoAgA2DXPUGnLjhVwEAAJlJrvoOnLjhVwEAABm5CvhOrgIAGCFXAeQqAIANchVArgIA2CBXAeQqAIANcpWN19e3A9cAAwy/CgAAyMbJVW+3i9lkKpfl7Wv12+1n53/HZr67qsDqh7fbxWy+frPbxdvtYvb53l+TN6bpjlAYfhUAAJCNl6ucWHC/mky9oHC6mkHNNlcVEUo019vtYjZJtuXeiVb2hl8FAABke8pV37+/rpeTxeb1+/c6l7xu5tPl7XpV9Gkl2zx+FT+LooqVxcvLEu4380Zn2Ot62eghkzGoX2nfX6uVMuh4/VWizGR7n8jKf39dL+X/dirqv1h9lg2YN1RVq/uVqDxsDL8KAADI9parRDiQuapMIXmiyn+ut3T6gdxkNptMV/ke7pMyJN2vqpXiZ2e0rko59atCpX3ffhadRvfJrFGgNg4o66C2Q6vX9ea++UIvSL1u5vUuYGP4VQAAQLa/XFXHFCdXiU6gxs9ORpHFOomn3szfviqt2p38rayPVppHCWrq/CpR2u4ByGlAESirYvc5Qe1DGH4VAACQHTpXqaN1xZZiUK9e5uu3cBKqh+TE3suS/eGzKgy156q8NytfYnLV92oosO8gYKgByVV7MPwqAAAgO/Q4YFeu0icSdfQw3SdyptTOuapIVI0Bvq7vAxbdVL0HAQXGAfdt+FUAAEB2+Hnr4VwVHJKLGrmTsWmncUAvzcTnqvzw10PSj9uAXs2Ztz6C4VcBAADZIZ6zEJ2r8nG9KkPcr0QXVNf8qmb3WOu89YjSGh1g4edXFSOYOw4CNhuQ5yyMbvhVAABAdsjngnbnKq8odQMnAJUjgOpjEdzSnOcsdJa2um/ODxMl+0HKmZK/A54Lum/DrwIAADL+js0omAJ1aoZfBQAAZOSqMbyul/QqnZbhVwEAABm5ylg+E4t55adm+FUAAEBGrgK+k6sAAEbIVQC5CgBgg1wFkKsAADbIVQC5CgBgwyBXvQEnbvhVAABAZpKr3v/5l4XlpJfhVwEAABm5ioXlnVwFADBCrmJhIVcBAGyQq1hYyFUAABvkKhYWchUAwAa5ioWFXAUAsHECuerp+eXg912W816GXwUAAGTj5KqX6/lsMvWXq6873PBeruezi5uXg993T2H5djVdXj8PeXn1ZiVfDn84e63V8KsAAIBsvFxlFIbIVfHLkFz17Wpat/PTzfI4otX+ajX8KgAAIDtErhK9WfPbp2r98+2F37kltvz0Lb/L1p1eX5PyLvtyPV9e3yST6WxSBAt9F083y7L8If064y2xB6K11b+DclXdmPFFvVzP/W2ebpZlPV+u5/m71q+EwbXacRl+FQAAkO09Vzm/ErdhJzN9+TQTmanaviVXydgR2IW8Sfs37CNZ4g4k2FZ2seP59qKtqHxsTt2grNvz7YUMgj1K2LlWg5bhVwEAANne5lcV+cAPNC/Xc23elZuZYnJVHeNCuzjSLOW3W/eBBNvKKleFu5qKfrKuTqZP3758Ckyniymhb60sluFXAQAA2Z77q8RIXCNyFcnAm6Qcm6uq9eFd1Glvpxn0e1giDyTUVia5qj1UxQTT4SX0KdNoGX4VAACQHSBX6cNDRUpodGvtlKvaRqDygbPjnGIVeSChturIVU5QC3dHtX1LIKq3Ka9eID/t0F/VWSuLZfhVAABAtu/5VaHBuK+JkyEG5Kq48b7j/Jph3IEE22pYf9XXJDrutM2OerpZXty85P/drYRdazVoGX4VAACQHWTeeh0LqrumzBBOl4YsSg4G5YN6Wq6K3cWx91f1b6sBuWqXBtG+zVeP9O34jcLBtdpxGX4VAACQHfg5C+KuWQ7P5Wmp7poqRq+KOFVNKlpef61u4c0J3Z27OM4pVjsciGyrOsp8+RTVG1dtps7l2qGJvnyqRxjlz30Lsa1VzDL8KgAAIDuJv2PD0nt5vr06ulHOo16GXwUAAGTkqrNcnm6S4xvlPOpl+FUAAEBGrmJheSdXAQCMkKtYWMhVAAAb5CoWFnIVAMAGuYqFhVwFALBBrmJhIVcBAGwY5Ko34MQNvwoAAMhMctV34MQNvwoAAMjIVcB3chUAwAi5CiBXAQBskKsAchUAwAa5CiBXAQBskKsAchUAwMY55KrX17cD12CPXl/fDlyDczT8KgAAIBsjV72ul5PprLl8vh/jhvh2u5jN129jFL1328/T5e1rywb7P9jt5/odXNVv4OtmLt/cxaat1oq320X52mSr/P51M3eb4j6pdtfeRDsafhUAAJCN21/VuDuO4JxyVac9H+z287Te3et6WUer+5Weh+LcJ1WcUo8oT131mXOfiG3uV07CMzL8KgAAINtrrnI7Ocruq7fbxfJ2vRJdEVUfSb6+uomKTo6ig8Tv9hBdZWPnuTFU/VXbz9Pl7X3VXPnKZh9Ps0GqciIb8LvW/iU/wdTdaffJgN5H96x4XS+97q7X9XKerOpt9pHOyVUAABt7y1Xbz2Io8D6pxpXebhfyNi/6SIocVm/m9J2IaFWslzlgnF6NkclcVY+73Scz5WCDDbJLA0YN5NXv5tvtYjnXI11fjf6q1818sXmVZ879atguogy/CgAAyA42DljnHvfO6t5E67EnPye93S7ylBbIVSfJyVV1h5DaVqEGGdKAbd5uF1U/mTM+WCSh3gdbdp45r327XSxvX50zJ4+A93VP5Chv8fCrAACAbO+5qjkPurrBlzdROXGnTAPqXPj5+q3ZhTPmHPmx9chVoQbZrQG7mkuGKrXaAxpcBL7X9VL0tIlcNWV+FQDgNOx1HLC+QbpZISpX6Z0iSndL+d2xk5ti1TNXaQ2yWwO2paLXzXza3qGllODEuI4Z7uXLZb9Xo7/qtbm9qeFXAQAA2f5ylTdLJpCrooexKqFhrFP8nuCQcUCxcf8GDMaU+5UST8Pz2aMoL599vtd71Jojm+QqAMAx22Ouqu6mxXzq+mtu4jYp85Ccvu1Or67v94GosZcvkVnrk6tiGiS6AfWYEmzDtigcIeLlzq4b2zMOCAA4VvubXyUe7bi6r6ND877uPibAeSKA8nDIop8j2bq7OMUpVp25yjnYUIP0bMBgrgp2IDm72O37gKEnRFT79iKdrDnz1gEAx+u4/47NXr5jf85owDjDrwIAALKjy1XOhJ5TnCN1aDTgToZfBQAAZEeXq9zhJzLBDmjAHQy/CgAAyI4wVwH7N/wqAAAgI1cB38lVAAAj5CqAXAUAsGGQq96AEzf8KgAAIDPJVQAAAMjIVQAAAFbIVQAAADbIVQAAADbIVQAAADbIVQAAADbIVQAAADbIVQAAADbIVQAAADbIVQAAADbIVQAAADbIVQAAADbIVQAAADbIVQAAADbIVQAAADbIVQAAADbIVQAAADbIVQAAADbIVQAAADbIVQAAADbIVQAAADbIVQAAADbIVQAAADbIVfbSND10FQAAwAGY5Kp0vZhNpu6yuLMJFw+ryXS1NSlqR4/J9HIdezDpejGbb9LyhbPkYbed/vXzT//95W+x4u8/fvzp9992K6zVb//59YefqsXdaWTdcn/+/sM4NQQA4FSY5So3QMh4Mczhc1Uvp5Wr/vr5p19/+M9f9Yo/f//hp19//nOnwshVAIAPb6RclWUPK9FlJTq0ZD9WejcXXVyihMekWHm53mi5Kr2bF7+aTaazSfKYPYif23aarhfVC/NeqEDdalV/1WMyvVw/VHVudmKJopLHIldt1O07d9qWq/7323+17qX3X67LbqfrP/5Xr/zvL7/9rvZF/fYfN1RVhRcv/+tnmbHq2CTr9tfPVU1+k7lKrQwAAGduD7nK6btKN5fleqc7Z5vMyvzkd/kEclUZofJElf+c560qLZUZa5vMZGW8wKfVTZK5qq6MKNNvCrXyXh26dhrOVbJbqP75/ZfrX3/87T1fLbLR+y/XoWQTGM5zNmjPVXKnecBqrwwAAGdupFz1mEzL6OAP5GkhTG7mba+OA6Z38zqTyXxW/pzezZ1XVdu4A5RRdXNyVf1bfYAyPA4YOkB9p3G5quKvfP/lOo9ETsRxdA8sduUqb6fV/wYrAwDAmRtt3nrZV5RuLv1fTeXUq2rIr+ja8ftv/IRUrayG1eS88jLKOKOQmYg7TojpqptXvk2uittpyzhgPcRWhRUxMlgvP/723pZpvFz19x8/+rPXO3KV3xFVFhiuDAAAZ86+v0qM6GVZcJwrqxKV162171zV/b3FEXJV9067562X3+PTIk6tpa8oMA749x8/Ds9VDPwBAD6kUcYBnWgV+kKfF316jwO25qrWccCubOQZexxQ1chDf/6uhZVymC/4Xby2MTh13np8rooeBwQA4KMYcX5VORToThV/WBXfjJPxovhiYHPKecu89dZc1TpvXVQ1UDeHda6K2mk+muZ8va4YSpOppc5A7vz0P3//QawPz23662fv+3rFaKAoswhe+eCjMm+93MCft65VBgCAMzfm9wG9aNV43MA2kTOrZAqptm99zkJbrnJ36n4BsPmorWbdhF65qpw+VT1nQd++c6dZ5j6xU85PkutFZhKPNqhzTPeccW86lLuxeIzCn9VApBxArHYafs6CCFXbxOipZgAAHCX+jg0AAIANchUAAIANchUAAIANchUAAIANchUAAIANchUAAIANchUAAIANg1z1BgAAcI4OkKve//n3XJfhjQMAAD4OchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAICNMXLVt6vpbOIvyZe4KPPl0+zq6+ETVVyuekyms8niLu3abpvMkofhLf2Y+K262g4v1S3fop4AAHxQe8tVs8n89ikiVE2m55artslsYpNX/NyzTaJS3c7lAwCAXsbLVbKDyl/zdLOs8laZol6u5yKEffpWrqle9e2qDmf5r5ZXn/JyltfP5cZfE6WH7Pn2Quk5a9YzJlel60VRVPLg5qqHlciRl+vU2XgynU2Sx8Bmvm0ym2+av2jknodV2WXl/spZf7l+uJs3d5eWK+tk9phMZ8lG2xgAAEQ4QK7KO6XkcnHzslOukj1h7pq6EK3/rChkh1zl5iQnlzQG6RZ3qZKr1M0iKf1V5f+25Kp6uFD0b1Xbp+tFleFCGwMAgCh7HAfMU07edVSPCTrhyR0HjMhVRXKq11zcvLz/8+973muVb+zvccA4YNHHUySPdHMZCEaNgKKPrzmbRWjOr3IiUShXKevrDfzytUIAAECUPeWqespUPU4nl+X18w65qnjVu7JGbuzVJ3YGvZKr8iG8fDgvy7T5VTL6tOQqZbMIfn9VurksR+v65ap0cxmKg+QqAAB2NvY4YJFpim6k0XOVurE3v8p7oVGuqqYrteeq8GYRmvPKqzXkKgAADm/8+VVlpinSUuuonJariv8tprrvlquCuzAbB8x/Lkbl3M1krmrZLIJZrmIcEACAMexj3nr57b/gvPUqANW/+vStdcs+ucrvrPL60ozmrTvf8lP6q4qOrvBmEbRxwKLbKV0vqo60vJKd3xMUUa94IbkKAIBB9vN9QH+auROYZK9SlYEaU6OuvlqNA7pzsAY8Z2G+uZPzq6r8NN+keb+UP/a3uEtbNhNanrMQzmTVb/MHK7TnKjkiWRVCrgIAYBD+jk2fcUAAAIAwchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANctWHyFVpmh66CqctpgH31shj7+ggBzLGTs/ytDc5qEO1TN/9nuU7GGMPB95rFx/2jdgNueokclW6XswmU7lcruvz/DFx/ld57XyTRmy5H1Ud5A+z5MF2F2qBux2+bMCYbYYcTmcNYyozxN7OFrmjloPa+SQZu6GGSNeL1ba5+mE1mWrrnRd2HVR6N+9RiN2lZ1L5Qdsfw4dbHL2tqrNiD6eu2MWhTpizRq46mVzlnM0Pq0ns+X1sN5jmx9/ectVu9pmrTCpzzOWrO4rZ6RnlqvQuUStmFE22CbnquKltVZ8V+81Vhzphzhq56jRzVZalm8vJ4i7NMucDJb2b5x1axa9ER1fy6H70iF8VG5dFPZSFyM+pquTpTES6dL24XG9W+cbzRb4XUUPxv5ncRai/Kt9L8Sq1hkrLaEcxSzZVhatPjc7D72zArjoUjSz3Lj/rO4/IbRz/jWhWRi3QeVP8F4r9ppvLSVv57ZWpm7pYuQncWZUzR+7ozt2pV3n3JNHfU3FpFHesyIZqtkBM5Xu08DbRbpBOD0GgATsa7TFYt/RuHjxR1bd453N1hMoH6xlTnz5Xd9u72XK2ywqqRQ24UoqzIrKhmmdgqPxmU7i72OsJ81GQq041V2Xp3TwYUEKdAdWW6VpkoG0yExGtvml566sKbJNqm3S9EFfRg389tw7GNaqd3s2dD476niRCpN8snUeRbi7Ln53D1wrvbMAQ/590WhvGHJHTJl2FhAp035TQZvLNqn9Wz5a2s0KMJsy0XNV25mgH4lVer4P7njZzVVxD6S0QW/nuFu4WOm1iGi20zc477Xuujl35xlmhXOlS/NWtVMz7V5nWJt6+1KJi2tPZRhPTUEqdtSux7SMiukvM6oT5QMhVJ5ur6kuu/EAJDts37pT+mLosSr1LufS7l/vy4LB9KFeJjwZl16FkGXEU3Q1VFt7dgCHhrvKqzJgjCk0nUhs8WKBb4d0PtqsyD6tG30/Xrb079zTPKHV+VecZG9FQ3UNXMZWPfGfbC1TL6dpvS1FtjM7V0SvfMgdIHY3qurpjKxb3GagXFdeeHWXGNFTjDFSvxMiPiA5WH24fCLnqfHJV3D8ry48eZ8tqm/bPlKqr2fn3kKzYNin+WRkYBMxCucrrVRYDNPXifxC0HYXfQS3XhwqPaMCQ7o+eqCPqk6vCBTpvSvtmjVGYHrnKf4vb7hb6mRPKVW5+8s4Wr55DGyowDtVd+YgW7uCfb1p6CDdaaJvu3Zqcq+NX3k3G+pUudVzd7RXTIrvTJppmUeH2bGur8IHH1Tl0Jbaf+Ya5audL4FyRq042VzXGAcfMVcWF3egAaFRMzBLI1zuXXHPWjrxti1pF9SQPyVVa4aPnqu6+8Z65Si+w8Znbut9tIkOtea5qO3P2l6t6tEBs5eNbOCR8u41ptNA23bs1OVfHr/yAXBWcgBXzIRaTq0JFmeeq6DMwlKvCHxHGuepjD/x5yFWnmquUeevjjQN6n2stuSpfs2n54AjnqraxG7VVrMYBm8flH9EI44CqIeOATmX6DWTUxVqPA7aeOT1zldU4YHsLxFa+ZwtrQsNDMY0W3KaT0bk6euWtxgHFXqI+xCJyVbAo63HA+DMwahxQ20U3qw+3D4RcdZq56mHlfwnFvfeIf8God8rQPNCIy6aYF1mXowS+acu351pyVb4jUUNnRnyzO6HtKLTJle7hK4V3NmBIxEdP1BH1yVXBAr03JbCZ/5727q/S/mGt3YHCZ07fXKW9p/IcyMf1ohtKb4HYyne3cDdZeXGAMY0W3CZqpxbn6tiVb7yDfeatR7zdoXczLlfpRbW2Z7OtdDENpZyB2pXY9hFhmat2vwTOE7nqZHKVO3odeC5o/aXc+roVQUcOpogyvScUaJ8p5VhJXrLTw6QNULZMWGnNVc1bpnK8gZYJPS1C+XJZuPCOBgx8c95v5NDncucRdUYZL7aqBeqdiM39ive0MVvIH7ENHZGYG7dZaXe70JnjHIj4uXUcUHlP3To81B0bEQ2lt0BE5Xu0cEwirxuw43LzT0V1G1n5Mc/VcSuftbyDvZ6zoL/dLe9m1PyqQFEx7Rl+Iol24NFnYOhK1JtC/dfv+CfMR0GuOolcdVK6H+B7KN4cnZ2EHuoIfxIMDo1z9WPa+UrkhDFCriJXGUs3l0f6TRB1rKdvGZvVB/+nWM3p7e81soB94Fz9KIyuRE4YK+QqcpWdfBDtKDstumZ9YRfyy56EKuBQuBKPCrmKXAUAAGyQq8hVAADMFysAAARaSURBVADABrmKXAUAAGyQq8hVAADABrmKXAUAAGyQq8hVAADABrmKXAUAAGyQq8hVAADABrmKXHVIaTr6I+z2sAsAAHLkKnLVDiz+0N4+/vJJeBcPq0M/m1j/W7OHYPJuAgCyjFxFrjqcQ+aqbXLwv2lDrgKAM0SuOolcla4Xl+tN3sWS3wLT9aL4a1Du3+N7TIq/EpVvv9r2ebn4I1P1jVZbKe/EalGPyfRy/XA3b5Qmjqh8VZ5v0mrj2aQOHM2aqweoVqOxi9I2qXZUtU/zEJq7DtRftr9+FGK900SzZNPSRMF3RN9L/leliwrPJslj1SdXHr73plRN1/luAgBikatOJVd5t/y6GybdXJa/ekyqga3i1ityQ+fLH0RMqX5WV9Z34nS9qFPLNpnJmlQvFOv9gyqr4XTebJNQzdsOUGuQmP6q0CF4uw7V3G9/7Siq9f4hdzRRsPG1veQNkh9InqjqwCojaVFgurlU303tuAAAschVJ5Or6nwgb7flb5OHLHtYNTqflNjR9nJnvbpxrrwTp3dz57fVLd8d5NILaZ/8FKi5eoChI4rJVcFDiKmet7vAZsE27Goi/YWBbdK7eV2gLDzwpjjrL9dp9HEBAMLIVSeTq6o7nBgbqpf5Jk03l86Al5tOOl8ux4DE3VRdKe7ETpdGlUV2y1XVGN8sWHPtANuPqCNXBQ8hmCrCu9OPItDxE9tEjcYPtFXdL5W5Q3uN/OQfabG+67gAAN3IVaeZq7QBmh65qnV8p5x+5Mz4cVea56oiJRT/21LzUK6KGLDzj3FIrtJ3px/FgFwlatuYYea3lUmuYuAPAIYhV51ergreg1vHASNv4XKPjUTi34nNxgG9cBPIVdHjgO1HkWXR44D6KFhc+xuMA6rHEtpLVK7qNQ4IAOiNXHWCucqbUv2wmijzjuUk5biXy9tqdZNWV8bNW++Xq5y9ON9b9GoeOsCuBnFEzlsPzC6KbECnhykvSnS59ZxfFXxHyr3E5Sptprz7birNCACIRa46xVyVOd+Hd25+7mMIghFBf7l4AIH3jTNvZcxzFro7Y4oJPclj5j/7oKXTSD3A4BHJXUju86tCz1lombXd2YDyKOSTEeTTDbqbqOsdEXuJ7K9KVtqbpb2b7nEx0QoAYpCrTiJX7cSfOXR2zv4AjR3Pk0gB4GyRq84oVzkDN3t4mvnenf0BjotcBQCjI1edUa5yHwFwlpnj7A9wTOQqABgdueqschUAADggchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2CBXkasAAIANchW5CgAA2DDIVW8AAADn6AC5CgAAABm5CgAAwAq5CgAAwAa5CgAAwAa5CgAAwAa5CgAAwAa5CgAAwMb/A5fFRufCNYrrAAAAAElFTkSuQmCC" alt="" width="677" height="236" />
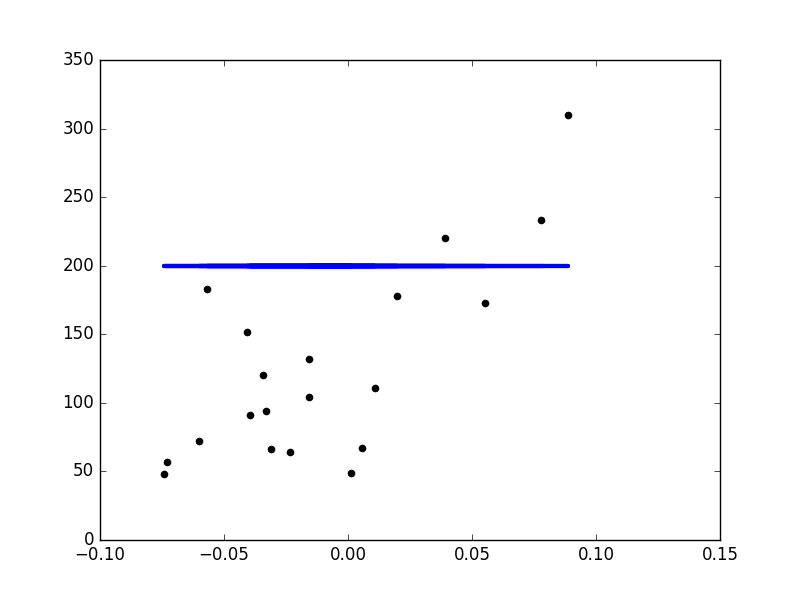
为了说明这个回归技术的一个二维图,例子仅仅使用了糖尿病数据集的第一个特征。
代码如下:
# -*- encoding:utf-8 -*-
"""
Line Regression Example
DataBase:diavetes
""" import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets,linear_model
import time a=time.time()
####加载数据集
diabetes=datasets.load_diabetes() ####仅仅使用一个特征:
diabetes_X=diabetes.data[:,np.newaxis,2] ###s数据划分训练集和测试集
diabetes_X_train=diabetes_X[:-20]
diabetes_X_test=diabetes_X[-20:] ###目标划分为训练集和测试集
diabetes_y_train=diabetes.target[:-20]
diabetes_y_test=diabetes.target[-20:] ###训练模型
regr=linear_model.LogisticRegression()
regr.fit(diabetes_X_train,diabetes_y_train) ###回归系数
print('Coefficients:\n',regr.coef_) ###均方误差
print('the mean sqare error:%.2f' %np.mean((regr.predict(diabetes_X_test)-diabetes_y_test)**2))
print('Variance score:%.2f' %regr.score(diabetes_X_test,diabetes_y_test))
##散点图
plt.scatter(diabetes_X_test,diabetes_y_test,color='black')
plt.plot(diabetes_X_test,regr.predict(diabetes_X_test),color='blue',linewidth=3)
plt.xticks()
plt.yticks()
b=time.time()
print('the running time is %.2f' %(b-a))
plt.show()
实验结果:
Coefficients:
[ 938.23786125]
Residual sum of squares: 2548.07
Variance score: 0.47
the running time is 0.31
Sklearn库例子2:分类——线性回归分类(Line Regression )例子的更多相关文章
- 从损失函数优化角度:讨论“线性回归(linear regression)”与”线性分类(linear classification)“的联系与区别
1. 主要观点 线性模型是线性回归和线性分类的基础 线性回归和线性分类模型的差异主要在于损失函数形式上,我们可以将其看做是线性模型在多维空间中“不同方向”和“不同位置”的两种表现形式 损失函数是一种优 ...
- Python机器学习笔记:sklearn库的学习
网上有很多关于sklearn的学习教程,大部分都是简单的讲清楚某一方面,其实最好的教程就是官方文档. 官方文档地址:https://scikit-learn.org/stable/ (可是官方文档非常 ...
- day-10 sklearn库实现SVM支持向量算法
学习了SVM分类器的简单原理,并调用sklearn库,对40个线性可分点进行训练,并绘制出图形画界面. 一.问题引入 如下图所示,在x,y坐标轴上,我们绘制3个点A(1,1),B(2,0),C(2,3 ...
- 复盘一篇讲sklearn库的文章(下)
skleran-处理流程 获取数据 以用sklearn的内置数据集, 先导入datasets模块. 最经典的iris数据集作为例子. from sklearn import datasets iris ...
- 复盘一篇讲sklearn库学习文章(上)
认识 sklearn 官网地址: https://scikit-learn.gor/stable/ 从2007年发布以来, scikit-learn已成为重要的Python机器学习库, 简称sklea ...
- 2.sklearn库中的标准数据集与基本功能
sklearn库中的标准数据集与基本功能 下面我们详细介绍几个有代表性的数据集: 当然同学们也可以用sklearn机器学习函数来挖掘这些数据,看看可不可以捕捉到一些有趣的想象或者是发现: 波士顿房价数 ...
- Python: sklearn库——数据预处理
Python: sklearn库 —— 数据预处理 数据集转换之预处理数据: 将输入的数据转化成机器学习算法可以使用的数据.包含特征提取和标准化. 原因:数据集的标准化(服从均值为 ...
- Python深度学习案例2--新闻分类(多分类问题)
本节构建一个网络,将路透社新闻划分为46个互斥的主题,也就是46分类 案例2:新闻分类(多分类问题) 1. 加载数据集 from keras.datasets import reuters (trai ...
- 分类and分类延展
1.Category简介 Category,又称为类别&类目&分类,是OC特有语法,在不修改原有类的基础上增加新的方法,一个庞大的类可以多人来分模块开发,有助于团队合作,或者对当前类方 ...
随机推荐
- JS 基础事件的用法
// 1.9以上用on // 案例一 // $('#btn').on('click', function(){ // //console.log(1); // alert('测试...'); // } ...
- Java三大主流开源工作流引擎技术分析
首先,这个评论是我从网上,书中,搜索和整理出来的,也许有技术点上的错误点,也许理解没那么深入.但是我是秉着学习的态度加以评论,学习,希望对大家有用,进入正题! 三大主流工作流引擎:Shark,oswo ...
- 神奇彩带KMP
描述 有两条彩带A,B,如果能制作出一条彩带,这条彩带既是彩带A的前缀,又是彩带B的后缀,称之为神奇彩带 草滩小王子想送一条最长的神奇彩带给拉面女神 给你两条彩带,你能找到最大的神奇彩带的长度是多少吗 ...
- Threads Events QObjects
Events and the event loop Being an event-driven toolkit, events and event delivery play a central ro ...
- shell MAC 地址 校验
/*************************************************************************************** * shell MAC ...
- 《more effective c++》条款26 限制类对象的个数
问题: 如何限制类对象的个数?比如1个,10个等等. 方法(1): 将类的构造函数定义为private,那么就无法实例化这个类了.但是如何创建1个对象出来?方法有2种: 1.声明一个友元函数,那么在友 ...
- LeetCode Rectangle Area (技巧)
题意: 分别给出两个矩形的左下点的坐标和右上点的坐标,求他们覆盖的矩形面积? 思路: 不需要模拟,直接求重叠的部分的长宽就行了.问题是如果无重叠部分,注意将长/宽给置为0. class Solutio ...
- <td colspan="2" > 一个td占两个 td空间
<tr> <td>机构名称: ${accreditInfo.companyName}</td> <td>初始授信额度: ${accreditInfo.i ...
- NIO中Selector分析
NIO中,使用Selector.select()方法来侦听是否有数据可以读/写,服务端开始执行时,如果没有客户端,这里的语句将进行阻塞,等待下面三个情况出现,才会进行后续的方法之行,这里是重点 ...
- Linux中的likely()和unlikely()
likely()与unlikely()在2.6内核中,随处可见,那为什么要用它们?它们之间有什么区别呢?首先明确: if (likely(value))等价于if (value) if (unlike ...
