通过Matrix进行二维图形仿射变换

Affine Transformation是一种二维坐标到二维坐标之间的线性变换，保持二维图形的“平直性”和“平行性”。仿射变换可以通过一系列的原子变换的复合来实现，包括：平移（Translation）、缩放（Scale）、翻转（Flip）、旋转（Rotation）和错切（Shear）。

在做2D图形引擎时，仿射变换是非常重要的点，图形的旋转等各种表现都需要通过仿射变换来完成，比如在显示列表树中，父节点旋转了，那么子节点在计算显示时也要叠加上父节点的变换矩阵，这是叠加矩阵。还有计算2D空间内的点在经过仿射变换的图形中的位置、鼠标是否点在经过仿射变换过的矩形中，等等都是需要仿射变换来完成计算。

定义一个矩阵类Matrix包含属性如下：

参数	描述
a	水平缩放比例
b	垂直倾斜比例
c	水平倾斜比例
d	垂直缩放比例
x	水平偏移像素
y	垂直偏移像素

矩阵的默认值为Matrix(1,0,0,1,0,0)，后面的变换以改变矩阵值的形式完成。通过H5中的canvas实现改变图形：

var c=document.getElementById("canvas");
var ctx=c.getContext("2d");

ctx.fillStyle="yellow";
ctx.fillRect(0,0,250,100)

var matrix = RM.Matrix.create(1,0,0,1,0,0);
ctx.setTransform(matrix.a,matrix.b,matrix.c,matrix.d,matrix.x,matrix.y);
ctx.fillStyle="red";
ctx.fillRect(0,0,250,100);

平移

平移变换是一种“刚体变换”，并不会改变图形的形状。

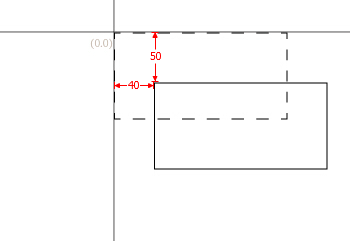
//（平移到点40,50）
matrix.translate( 40, 50 );

涉及到函数的平移公式code：

/**平移x，y像素*/
public translate( x:number, y:number ):RM.Matrix {
    this.x += x;
    this.y += y;
    return this;
}

缩放

缩放变换可以改变图形的宽高比例，横向缩放与纵向缩放。当值为负数时反向缩放。

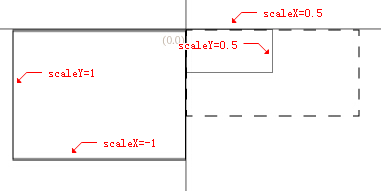
//（x轴缩放0.5，y轴缩放0.5）
matrix.scale( 0.5, 0.5 );
或
//（x轴缩放-1，y轴缩放1）
matrix.scale( -1, 1 );

涉及到函数的缩放公式code：

/**缩放，x、y轴方向缩放*/
public scale( scaleX:number, scaleY:number ):RM.Matrix {
    this.a *= scaleX;
    this.b *= scaleY;
    this.c *= scaleX;
    this.d *= scaleY;
    this.x *= scaleX;
    this.y *= scaleY;
    return this;
}

旋转

目标图形围绕(x,y)点顺时针旋转value弧度

旋转矩阵为(cosA, sinA, -sinA, cosA, 0, 0)

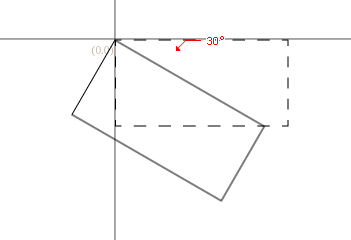
//（顺时针旋转30角度）
matrix.rotate( 30 );

涉及到函数的旋转公式code：

/**旋转，单位是角度
 * 旋转矩阵（ cosA, sinA, -sinA, cosA, 0, 0）
 * */
public rotate( angle:number ):RM.Matrix {
    angle = ( angle % 360 )
    angle = RM.GFunction.angle2radian( angle );//角度转弧度
    var cos:number = Math.cos( angle );
    var sin:number = Math.sin( angle );
    var ta:number = this.a;
    var tc:number = this.c;
    var tx:number = this.x;
    this.a = ta * cos - this.b * sin;
    this.b = ta * sin + this.b * cos;
    this.c = tc * cos - this.d * sin;
    this.d = tc * sin + this.d * cos;
    this.x = tx * cos - this.y * sin;
    this.y = tx * sin + this.y * cos;
    return this;
}

错切

错切变换指的是类似于四边形不稳定性那种性质，菱形形状。根据弧度顺时针倾斜。

错切矩阵为( 1, tanAy, tanAx, 1, 0, 0 )

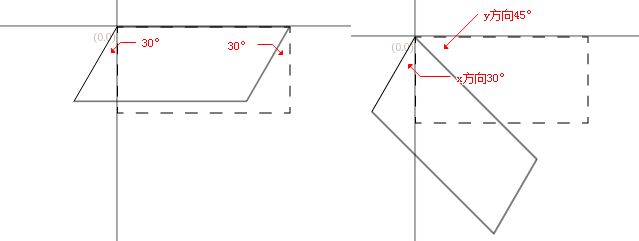
//（x轴错切30角度）
matrix.skew( 30, 45 );

涉及到函数的错切公式code：

/**切变，单位是角度
 * 切变矩阵 （ 1, tanAy, tanAx, 1, 0, 0）
 * */
public skew( angleX:number, angleY:number ):RM.Matrix {
    angleX = ( angleX % 90 );
    angleY = ( angleY % 90 );
    angleX = RM.GFunction.angle2radian( angleX );//角度转弧度
    angleY = RM.GFunction.angle2radian( angleY );//角度转弧度
    var tanAx:number = Math.tan( angleX );
    var tanAy:number = Math.tan( angleY );
    var ta:number = this.a;
    var tc:number = this.c;
    var tx:number = this.x;
    this.a = ta + tanAx * this.b;
    this.b = ta * tanAy + this.b;
    this.c = tc + tanAx * this.d;
    this.d = tc * tanAy + this.d;
    this.x = tx + tanAx * this.y;
    this.y = tx * tanAy + this.y;
    return this;
}

属性叠加

当设置仿射变换的多个属性时，依据矩阵乘法的特性要遵循顺序（缩放->错切->旋转－>平移）依次变换。

如果不按照以上顺序，产生的结果将会与预期大大不同。下图以先x轴缩放0.5、错切x轴-30y轴30、旋转10度、平移（10，20）

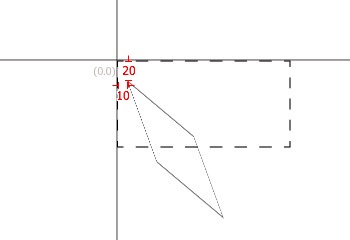
错切与旋转的区别：错切可以分别向两方向倾斜不同的角度；旋转是同时向两方向倾斜相同的角度。

那么，可以把错切与旋转合并，错切的默认x轴倾斜是正方向倾斜，也就是逆时针，改为与y轴倾斜相同的顺时针方向。

当旋转30度时，也就是x轴y轴同时顺时针倾斜30度。

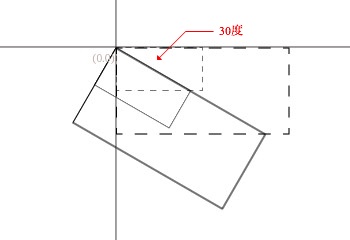
如图所示，大矩形错切x轴y轴各30度，小矩形旋转30度，两者的结果是一致的。

//大矩形
matrix.rightTransform( 0,0,1,1,30,30,0 );
//小矩形
matrix.rightTransform( 0,0,1,1,0,0,30 );

属性叠加公式code：

/**转换矩阵操作，顺序为：缩放、切变、旋转、平移*/
public rightTransform(x:number, y:number, scaleX:number, scaleY:number, skewX:number, skewY:number, rotate:number):RM.Matrix {
    rotate = ( rotate % 360 );
    rotate = RM.GFunction.angle2radian(rotate);
    //旋转与切变一起算
    skewX = RM.GFunction.angle2radian(skewX) + rotate;
    skewY = RM.GFunction.angle2radian(skewY) + rotate;
    if (skewX || skewY) {
        //矩阵乘法（右置矩阵、后置矩阵）
        this.rightMultiply(Math.cos(skewY) * scaleX, Math.sin(skewY) * scaleX, -Math.sin(skewX) * scaleY, Math.cos(skewX) * scaleY, x, y);
    }
    else {
        this.rightMultiply(scaleX, 0, 0, scaleY, x, y);
    }
}

叠加矩阵

在显示对象树中，父节点旋转30度，那么它的子节点是否也要旋转到相对于父节点的位置呢？答案是肯定的，必须旋转到相对位置。这就涉及到矩阵乘法，例如矩阵A*矩阵B得到的就是叠加矩阵，但是一定要注意的是 A*B ≠ B*A 。

矩阵乘法满足结合律，但不满足交换律。

因为矩阵A*B=C，C的结果是由A的行与B的列相乘和的结果；而B*A=D，D的结果是由B的行与A的列相乘和的结果。显然，得到的结果C和D不一定相等。

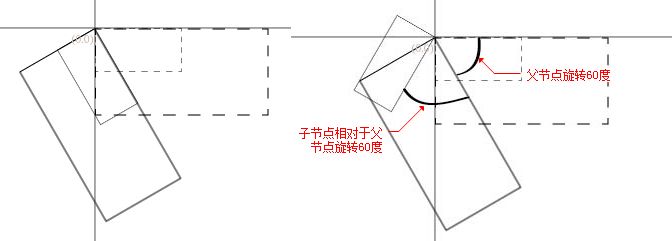
显然，大矩形为父节点，小矩形为大矩形的子节点，当大矩形旋转60度时，小矩形相对于父节点为0度，

然后小矩形再旋转60度，这是相对于父节点旋转了60度，相对于原点旋转了120度。大矩形以原点(0,0)点旋转，小矩形以大矩形内的坐标(0,0)点旋转。

parent.matrix = RM.Matrix.create(0,0,1,1,0,0,60);
//父节点的矩阵与子节点的矩阵相乘，便是子节点的真实矩阵
child.matrix = parent.matrix.rightTransform(0,0,1,1,0,0,60);

矩阵的运用

矩阵这东西在图形引擎中的运用是很多的，上面的例图就是使用自己写好的图形引擎，通过设置属性再渲染到canvas中的。一张坐标轴地图、一个虚线矩形、一个实线矩形完成演示。

矩阵的运用还是很多的，2D图形引擎中坐标点的判断，鼠标点击是否在图形上，脏矩形的范围，子节点上的坐标与原点坐标系的转换，等都是通过点与矩阵之间的二维空间转换而得到确切的值。