[AGC004F] Namori

Description

现在给你一张N个点M条边的连通图，我们保证N−1≤M≤N，且无重边和自环。

每一个点都有一种颜色，非黑即白。初始时，所有点都是白色的。

“全”想通过执行若干次某种操作的方式，来将所有的点变成黑色。操作方式如下：

选择一对颜色相同的相邻的节点（存在边直接连接彼此），将它们的颜色反转。即若原来都是白色，则都变成黑色，反之亦然。

现在“全”想知道，他能否通过执行这种操作以达到目的。如果可以，他还希望步数尽可能的少。

Input

第一行有两个正整数N和M（2≤N≤105，N−1≤M≤N）

接下来M行，每行2个正整数a和b（1≤a,b≤N），表示每条边连接的两个点。

Output

如果存在操作方案使得“全”能达到目的，请输出最少操作次数。

否则，请输出−1

题解：

这里

分三类：树，奇环，偶环

1.树

我们可以吧两个相邻的两个颜色相同的点翻转转化为，我们把原树二分图染色，把两个相邻的两个不同颜色的点交换。那我们的目标就是把所有黑点变成白点，白点变为黑点

我们可以看做一个球入洞的问题，白点上都有一个球，黑点上都有一个洞。我们把每个球都放进一个洞里，问最小要移多少次才能使全部球都入洞。

那么方案可行的条件是球和洞的数量相等。

那么我们把白点权值设为1，黑点为-1，那么答案就为

\[\sum_i sum_i
\]

\(sum_i\) 为子树 \(i\) 的点权和（仔细想想能明白的）。

以上就是为树的解法。

2.奇环

奇环只不过是在树上加一条边罢了。

奇环多出来的那条边的两端肯定是同色的，所以对这条边操作一次可以使两个端点同时加上或是减少若干个球。

那我们如果图中球数和洞数不一样的话，我们可以通过操作这条边补成相等。

就像这样：

if(sum&1)return printf("-1"),0;	//sum为球数和洞数的差
ans+=abs(sum>>1);
siz[S]-=sum>>1,siz[T]-=sum>>1;

奇环卒……

3.偶环：

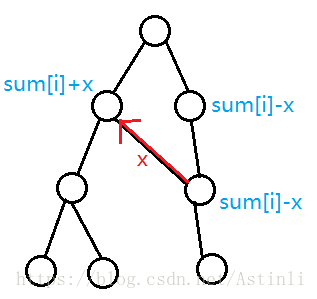
偶环条的两个端点不是同一种颜色的，那我们可以从一个点运 \(x\) 个球到另一个点。

那我们其中一个点到 \(lca\) 的 \(sum\) 都要加 \(x\)，另一边要减 \(x\)。

如图：

我们可以得到这些修改后的sum[i]。

我们换一下顺序全部写成 \(x-k[i]*sum[i]\) 的形式。

答案就为那些不受影响到点的sum和，加上 \(\sum_i |x-k[i]*sum[i]|\)

这不是初中的典型数学问题吗？找到一个x使得他到他到数轴上其他n个点的距离最小，

取中位数就行了。

AC……

COMPLETE CODE：

#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstdio>
using namespace std;

long long ans=0;
int tot=0,h[100005];
int n,m,x,y,S,T,k[100005],siz[100005];
int s[100005],top;
bool odd;
struct Edge{
	int x,next;
}e[200005];

inline void add_edge(int x,int y){
	e[++tot].x=y;
	e[tot].next=h[x],h[x]=tot;
}

void dfs1(int x,int fa){
	for(int i=h[x];i;i=e[i].next){
		if(e[i].x==fa)continue;
		if(siz[e[i].x]){
			if(siz[x]==siz[e[i].x])odd=true;
			S=x,T=e[i].x;
		}else{
			siz[e[i].x]=-siz[x];
			dfs1(e[i].x,x);
		}
	}
}

void dfs2(int x,int fa){
	for(int i=h[x];i;i=e[i].next){
		if(e[i].x==fa||(x==S&&e[i].x==T)||(x==T&&e[i].x==S))continue;
		dfs2(e[i].x,x);
		siz[x]+=siz[e[i].x];
		k[x]+=k[e[i].x];
	}
}

int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		scanf("%d%d",&x,&y);
		add_edge(x,y);
		add_edge(y,x);
	}
	siz[1]=1,dfs1(1,0);
	int sum=0;
	for(int i=1;i<=n;i++)sum+=siz[i];
	if(m==n-1){
		if(sum)return printf("-1"),0;
	}else{
		if(odd){
			if(sum&1)return printf("-1"),0;
			ans+=abs(sum>>1);
			siz[S]-=sum>>1,siz[T]-=sum>>1;
		}else{
			if(sum)return printf("-1"),0;
			else k[S]=1,k[T]=-1;
		}
	}
	dfs2(1,0);
	for(int i=1;i<=n;i++){
		if(k[i])s[++top]=k[i]*siz[i];
		else ans+=abs(siz[i]);
	}
	s[++top]=0;
	sort(s+1,s+top+1);
	int mid=s[top+1>>1];
	for(int i=1;i<=top;i++)ans+=abs(s[i]-mid);
	printf("%lld",ans);
}