洛谷P4363 [九省联考2018]一双木棋chess 【状压dp】

题目

菲菲和牛牛在一块n 行m 列的棋盘上下棋，菲菲执黑棋先手，牛牛执白棋后手。棋局开始时，棋盘上没有任何棋子，两人轮流在格子上落子，直到填满棋盘时结束。

落子的规则是：一个格子可以落子当且仅当这个格子内没有棋子且这个格子的左侧及上方的所有格子内都有棋子。

棋盘的每个格子上，都写有两个非负整数，从上到下第i 行中从左到右第j 列的格子上的两个整数记作$A_{i,j}$、$B_{i,j}$。在游戏结束后，菲菲和牛牛会分别计算自己的得分：菲菲的得分是所有有黑棋的格子上的 $A_{i,j}$之和，牛牛的得分是所有有白棋的格子上的 $B_{i,j}$的和。

菲菲和牛牛都希望，自己的得分减去对方的得分得到的结果最大。现在他们想知道，在给定的棋盘上，如果双方都采用最优策略且知道对方会采用最优策略，那么，最终的结果如何。

输入格式

从文件chess.in 中读入数据。

输入第一行包含两个正整数n;m，保证n;m <= 10。

接下来n 行，每行m 个非负整数，按从上到下从左到右的顺序描述每个格子上的第一个非负整数：其中第i 行中第j 个数表示 $A_{i,j}$ 。

接下来n 行，每行m 个非负整数，按从上到下从左到右的顺序描述每个格子上的第二个非负整数：其中第i 行中第j 个数表示 $B_{i,j}$ 。

输出格式

输出到文件chess.out 中。

输出一个整数，表示菲菲的得分减去牛牛的得分的结果。

输入样例

2 3

2 7 3

9 1 2

3 7 2

2 3 1

输出样例

提示

样例1说明：

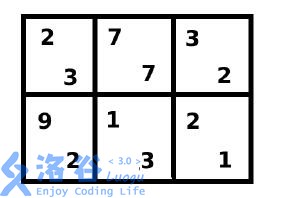
棋盘如图所示，双方都采用最优策略时，棋局如下：

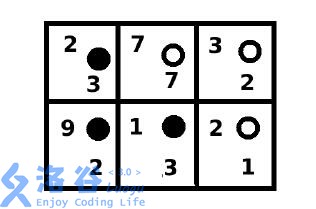
• 菲菲下在第1 行第1 列（这是第一步时唯一可以落子的格子）；

• 牛牛下在第1 行第2 列；

• 菲菲下在第2 行第1 列；

• 牛牛下在第1 行第3 列；

• 菲菲下在第2 行第2 列；

• 牛牛下在第2 行第3 列（这是这一步时唯一可以落子的格子）；

• 填满棋盘，游戏结束，盘面如下。

菲菲的得分为：2 + 9 + 1 = 12 ；牛牛的得分为：7 + 2 + 1 = 10 。

对于所有的测试数据，$n,m <= 10 ， A_{i,j},B_{i,j}<= 100000$。

对于编号为奇数的测试点，保证所有的 $B_{i,j} = 0 $。

题解

范围很小，很容易想到状压dp

但是$2^{10 * 10}$有点大啊

根据题目的性质，每行从左取而且取的数量乘单调递增，似乎状态数少了很多

于是对于这种单调递增的矩阵取数，有一种状压方法叫做轮廓线状压

我们先放置$m$个$0$，再向其中插入$n$个$1$，每个$1$代表一行，每个$1$右边有几个$0$就代表了这行选了几个数

由于单调性，所以每个$1$对应的行唯一确定

就可以记忆化搜索转移了

#include<iostream>

#include<cstdio>

#include<cmath>

#include<cstring>

#include<algorithm>

#define LL long long int

#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)

#define REP(i,n) for (int i = 1; i <= (n); i++)

#define BUG(s,n) for (int i = 1; i <= (n); i++) cout<<s[i]<<' '; puts("");

using namespace std;

const int maxn = 12,maxm = 1 << 22,INF = 1000000007;

inline int read(){

	int out = 0,flag = 1; char c = getchar();

	while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}

	while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}

	return out * flag;

}

int A[maxn][maxn],B[maxn][maxn],f[maxm],vis[maxm],n,m;

int F(int s,int p){

	if (vis[s]) return f[s];

	int re = p ? -INF : INF;

	vis[s] = true;

	for (int i = 0,j = n + 1,k = 1; i < n + m; i++){

		if ((s | (1 << i)) != s) k++;

		else j--;

		if (i == n + m - 1 || ((s >> i) & 3) != 1) continue;

		int e = (s ^ (3 << i));

		if (p) re = max(re,F(e,p ^ 1) + A[j][k]);

		else re = min(re,F(e,p ^ 1) - B[j][k]);

	}

	return f[s] = re;

}

int main(){

	n = read(); m = read();

	REP(i,n) REP(j,m) A[i][j] = read();

	REP(i,n) REP(j,m) B[i][j] = read();

	f[((1 << n) - 1) << m] = 0;

	vis[((1 << n) - 1) << m] = true;

	printf("%d\n",F((1 << n) - 1,1));

	return 0;

}