CodeForces - 922E Birds —— DP

题目链接：https://vjudge.net/problem/CodeForces-922E

E. Birds

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Apart from plush toys, Imp is a huge fan of little yellow birds!

To summon birds, Imp needs strong magic. There are n trees in a row on an alley in a park, there is a nest on each of the trees. In the i-th nest there are ci birds; to summon one bird from this nest Imp needs to stay under this tree and it costs him costi points of mana. However, for each bird summoned, Imp increases his mana capacity by B points. Imp summons birds one by one, he can summon any number from 0 to ci birds from the i-th nest.

Initially Imp stands under the first tree and has W points of mana, and his mana capacity equals W as well. He can only go forward, and each time he moves from a tree to the next one, he restores X points of mana (but it can't exceed his current mana capacity). Moving only forward, what is the maximum number of birds Imp can summon?

Input

The first line contains four integers n, W, B, X (1 ≤ n ≤ 103, 0 ≤ W, B, X ≤ 109) — the number of trees, the initial points of mana, the number of points the mana capacity increases after a bird is summoned, and the number of points restored when Imp moves from a tree to the next one.

The second line contains n integers c1, c2, ..., cn (0 ≤ ci ≤ 104) — where ci is the number of birds living in the i-th nest. It is guaranteed that .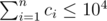

The third line contains n integers cost1, cost2, ..., costn (0 ≤ costi ≤ 109), where costi is the mana cost to summon a bird from the i-th nest.

Output

Print a single integer — the maximum number of birds Imp can summon.

Examples

input

Copy

2 12 0 4
3 4
4 2

output

6

input

Copy

4 1000 10 35
1 2 4 5
1000 500 250 200

output

5

input

Copy

2 10 7 11
2 10
6 1

output

11

Note

In the first sample base amount of Imp's mana is equal to 12 (with maximum capacity also equal to 12). After he summons two birds from the first nest, he loses 8 mana points, although his maximum capacity will not increase (since B = 0). After this step his mana will be 4 of 12; during the move you will replenish 4 mana points, and hence own 8 mana out of 12 possible. Now it's optimal to take 4 birds from the second nest and spend 8 mana. The final answer will be — 6.

In the second sample the base amount of mana is equal to 1000. The right choice will be to simply pick all birds from the last nest. Note that Imp's mana doesn't restore while moving because it's initially full.

题意：

有n棵树，在第i棵树上有ci只小鸟，在此树召唤一只小鸟需要花费costi个mama，但却能增加b个单位装mama的容量。人初始时在第一棵树下，且只能往前走，但每往前走一棵树，就能得到x个mama，前提是不能超过容量，初始容量和mama值都为w。问在第n棵树时，最多能召唤多少只小鸟。

题解：

1.一看题目，就很容易想到DP递推：设 dp[i][cnt]为到达第i棵树，且剩余cnt个mama的情况下，最多能召唤多少只小鸟。

2.但是，在看看数据：w、cost等有关mama的大小范围都为：1e9，数组根本开不了这么大。而却规定了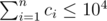：，多么（找不到形容词）。

3.根据数据范围，重新调整一下dp数组，设dp[i][j]为：到达第i棵树，且召唤了j只小鸟所剩下的mama的最大值。

4.那么就可以根据此递推。

代码如下：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int MOD = 1e9+;
 const int MAXN = 1e5+;

 LL dp[][];    //直接开1e3*1e4，内存开销太大，故使用滚动数组
 int c[], cost[];
 int main()
 {
     int n, w, b, x;
     while(scanf("%d%d%d%d", &n,&w,&b,&x)!=EOF)
     {
         int sum = ;
         for(int i = ; i<=n; i++) scanf("%d", &c[i]), sum += c[i];
         for(int i = ; i<=n; i++) scanf("%d", &cost[i]);

         memset(dp, -, sizeof(dp));
         for(int j = ; j<=c[]; j++)    //初始化第一棵树
             dp[][j] = 1LL*w-1LL*j*cost[];
         for(int i = ; i<=n; i++)
         {
             memset(dp[i&], -, sizeof(dp[i&]));   //记得初始化
             for(int j = ; j<=sum; j++)
             {
                 for(int k = ; k<=min(j,c[i]); k++)
                 {
                     //小于0，即不可能达到的状态，必须退出。否则往后可能又会变成正，认为此状态是存在的，对答案有影响。
                     if(dp[(i-)&][j-k]<) continue;
                     LL tmp = min(1LL*w+1LL*(j-k)*b, dp[(i-)&][j-k]+x)-1LL*k*cost[i];
                     dp[i&][j] = (dp[i&][j]==-)?tmp:max(dp[i&][j],tmp);
                 }
             }
         }

         int cnt = sum;
         while(cnt && dp[n&][cnt]<) cnt--;
         printf("%d\n", cnt);
     }
 }