CodeForces 781E Andryusha and Nervous Barriers 线段树 扫描线

题意：

有一个\(h \times w\)的矩形，其中有\(n\)个水平的障碍。从上往下扔一个小球，遇到障碍后会分裂成两个，分别从障碍的两边继续往下落。

如果从太高的地方落下来，障碍会消失。

问从每一列的上方扔一个小球，最终落到下面有多少个球。

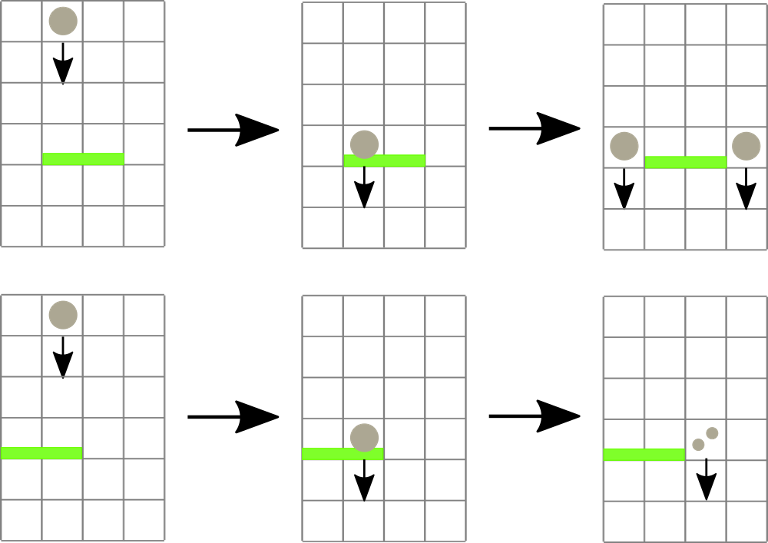
分析：

每一个障碍对应一个矩形，也就是它的有效范围，在这个范围内下落的球才会落到上面，否则障碍会消失。

维护一条从下往上的扫描线，用线段树维护\([1,w]\)区间内被障碍覆盖的集合。

在扫描的过程中计算出对每个障碍一个球落在上面最终会形成多少个球，这可以通过在线段树中查询所在区间中最高的障碍来递推。

扫描结束后，也可以用同样的方法求出每个位置落下最终形成的球数。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <set>
using namespace std;

const int maxn = 100000 + 10;
const int maxnode = maxn << 2;
const int MOD = 1000000007;

int h, w, n;

struct Barrier
{
	int l, r, h, s;

	void read() { scanf("%d%d%d%d", &h, &l, &r, &s); }
};

struct Event
{
	int height, type, id;

	bool operator < (const Event& t) const {
		return height < t.height || (height == t.height && type < t.type);
	}
};

struct Node
{
	int h, id;
	bool operator < (const Node t) const {
		return h > t.h;
	}
};

Barrier barriers[maxn];
Event events[maxn << 1];
set<Node> S[maxnode];
int cnt[maxn], ans[maxn];

void add(int& a, int b) { a += b; if(a >= MOD) a -= MOD; }

int op, id, height;

void opt(int o, int L, int R, int qL, int qR) {
	if(qL <= L && R <= qR) {
		if(op == 0) S[o].erase((Node){ height, id });
		else S[o].insert((Node){ height, id });
		return;
	}
	int M = (L + R) / 2;
	if(qL <= M) opt(o<<1, L, M, qL, qR);
	if(qR > M) opt(o<<1|1, M+1, R, qL, qR);
}

Node qans;
void query(int o, int L, int R, int p) {
	if(!S[o].empty()) { Node tmp = *S[o].begin(); if(tmp < qans) qans = tmp; }
	if(L == R) return;
	int M = (L + R) / 2;
	if(p <= M) query(o<<1, L, M, p);
	else query(o<<1|1, M+1, R, p);
}

int query(int p)
{
	qans = (Node){ -1, -1 };
	query(1, 1, w, p);
	if(qans.id == -1) return 1;
	else return ans[qans.id];
}

int main()
{
	int tot = 0;
	scanf("%d%d%d", &h, &w, &n);
	for(int i = 0; i < n; i++) {
		Barrier& b = barriers[i];
		b.read();
		events[tot++] = (Event){ b.h, 1, i };
		if(b.h + b.s <= h) events[tot++] = (Event){ b.h + b.s + 1, -1, i };
	}
	sort(events, events + tot);
	for(int i = 0; i < tot; i++) {
		id = events[i].id;
		Barrier& b = barriers[id];
		if(events[i].type == -1) {
			op = 0; height = b.h;
			opt(1, 1, w, b.l, b.r);
		} else {
			if(b.l == 1) ans[id] = query(b.r + 1) * 2 % MOD;
			else if(b.r == w) ans[id] = query(b.l - 1) * 2 % MOD;
			else ans[id] = (query(b.l - 1) + query(b.r + 1)) % MOD;
			op = 1; height = b.h;
			opt(1, 1, w, b.l, b.r);
		}
	}

	int res = 0;
	for(int i = 1; i <= w; i++) add(res, query(i));
	printf("%d\n", res);

	return 0;
}