Leetcode 391.完美矩形

完美矩形

我们有 N 个与坐标轴对齐的矩形, 其中 N > 0, 判断它们是否能精确地覆盖一个矩形区域。

每个矩形用左下角的点和右上角的点的坐标来表示。例如， 一个单位正方形可以表示为 [1,1,2,2]。 ( 左下角的点的坐标为 (1, 1) 以及右上角的点的坐标为 (2, 2) )。

示例 1:

rectangles = [

[1,1,3,3],

[3,1,4,2],

[3,2,4,4],

[1,3,2,4],

[2,3,3,4]

]

返回 true。5个矩形一起可以精确地覆盖一个矩形区域。

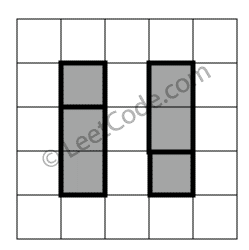
示例 2:

rectangles = [

[1,1,2,3],

[1,3,2,4],

[3,1,4,2],

[3,2,4,4]

]

返回 false。两个矩形之间有间隔，无法覆盖成一个矩形。

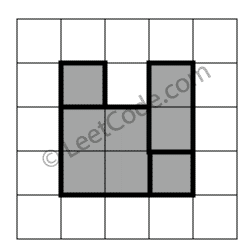
示例 3:

rectangles = [

[1,1,3,3],

[3,1,4,2],

[1,3,2,4],

[3,2,4,4]

]

返回 false。图形顶端留有间隔，无法覆盖成一个矩形。

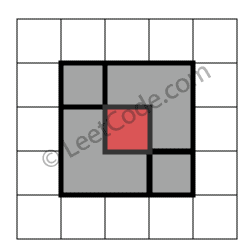
示例 4:

rectangles = [

[1,1,3,3],

[3,1,4,2],

[1,3,2,4],

[2,2,4,4]

]

返回 false。因为中间有相交区域，虽然形成了矩形，但不是精确覆盖。

核心思想就是:能够正好围成一个矩形的情况就是:
有且只有:
- 最左下 最左上 最右下 最右上 的四个点只出现过一次,其他肯定是成对出现的(保证完全覆盖)
- 上面四个点围成的面积,正好等于所有子矩形的面积之和(保证不重复)

 import java.util.HashSet;

 /** * 核心思想就是:能够正好围成一个矩形的情况就是:
  * 有且只有:
  * - 最左下 最左上 最右下 最右上 的四个点只出现过一次,其他肯定是成对出现的(保证完全覆盖)
  * - 上面四个点围成的面积,正好等于所有子矩形的面积之和(保证不重复)
  * Created by MebiuW on 16/8/29. */

 public class Solution{
     public boolean isRectangleCover(int[][] rectangles){
         int left=Integer.MAX_VALUE;
         int right=Integer.MIN_VALUE;
         int top=Integer.MIN_VALUE;
         int bottom=Integer.MAX_VALUE;
         int n=rectangles.length;
         HashSet<String> flags=new HashSet<String>();
         int totalArea=0;
         for(int i=0;i<n;i++){
             left=Math.min(left,rectangles[i][0]);
             bottom=Math.min(bottom,rectangles[i][1]);
             right=Math.max(right,rectangles[i][2]);
             top=Math.max(top,rectangles[i][3]);
             totalArea+=(rectangles[i][3]-rectangles[i][1])*(rectangles[i][2]-rectangles[i][0]);
             String pointLT=rectangles[i][0]+" "+rectangles[i][3];
             String pointLB=rectangles[i][0]+" "+rectangles[i][1];
             String pointRT=rectangles[i][2]+" "+rectangles[i][3];
             String pointRB=rectangles[i][2]+" "+rectangles[i][1];
             if(!flags.contains(pointLT)) flags.add(pointLT);
             else flags.remove(pointLT);
             if(!flags.contains(pointLB)) flags.add(pointLB);
             else flags.remove(pointLB);
             if(!flags.remove(pointRT)) flags.add(pointRT);
             else flags.remove(pointRT);
             if(!flags.contains(pointRB)) flags.add(pointRB);
             else flags.remove(pointRB);
         }
         if(flags.size()==4&&flags.contains(left+" "+top)
                 &&flags.contains(left+" "+bottom)
                 &&flags.contains(right+" "+bottom)
                 &&flags.contains(right+" "+top)){
             return totalArea==(right-left)*(top-bottom);
         }
         return false;
     }
 }