POJ Code the Tree 树的pufer编号

Code the Tree

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 2259		Accepted: 859

Description

A tree (i.e. a connected graph without cycles) with vertices numbered by the integers 1, 2, ..., n is given. The "Prufer" code of such a tree is built as follows: the leaf (a vertex that is incident to only one edge) with the minimal number is taken. This leaf, together with its incident edge is removed from the graph, while the number of the vertex that was adjacent to the leaf is written down. In the obtained graph, this procedure is repeated, until there is only one vertex left (which, by the way, always has number n). The written down sequence of n-1 numbers is called the Prufer code of the tree.
Your task is, given a tree, to compute its Prufer code. The tree is
denoted by a word of the language specified by the following grammar:

T ::= "(" N S ")"

S ::= " " T S

    | empty

N ::= number

That is, trees have parentheses around them, and a number denoting
the identifier of the root vertex, followed by arbitrarily many (maybe
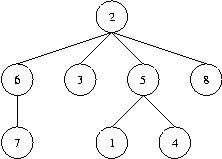
none) subtrees separated by a single space character. As an example,
take a look at the tree in the figure below which is denoted in the
first line of the sample input. To generate further sample input, you
may use your solution to Problem 2568.

Note that, according to the definition given above, the root of a
tree may be a leaf as well. It is only for the ease of denotation that
we designate some vertex to be the root. Usually, what we are dealing
here with is called an "unrooted tree".

Input

The
input contains several test cases. Each test case specifies a tree as
described above on one line of the input file. Input is terminated by
EOF. You may assume that 1<=n<=50.

Output

For
each test case generate a single line containing the Prufer code of the
specified tree. Separate numbers by a single space. Do not print any
spaces at the end of the line.

Sample Input

(2 (6 (7)) (3) (5 (1) (4)) (8))
(1 (2 (3)))
(6 (1 (4)) (2 (3) (5)))

Sample Output

5 2 5 2 6 2 8
2 3
2 1 6 2 6

Source

Ulm Local 2001

 

应该是水题，所以连边表都没开，那set乱搞，然后就Wa了一个小时。

注意整行读入的格式：cin.getline(str,MAXL,'\n')

priority_queue的比较函数自定义：priority_queue<int,vector<int>,cmp_c> q;

还有就是普通数组储存的序列输出，在序列为空时要特判。