PAT_A1146#Topological Order

Source:

PAT A1146 Topological Order (25 分)

Description:

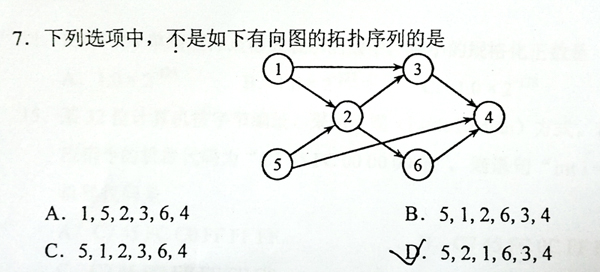
This is a problem given in the Graduate Entrance Exam in 2018: Which of the following is NOT a topological order obtained from the given directed graph? Now you are supposed to write a program to test each of the options.

Input Specification:

Each input file contains one test case. For each case, the first line gives two positive integers N (≤1,000), the number of vertices in the graph, and M (≤ 10,000), the number of directed edges. Then M lines follow, each gives the start and the end vertices of an edge. The vertices are numbered from 1 to N. After the graph, there is another positive integer K (≤ 100). Then K lines of query follow, each gives a permutation of all the vertices. All the numbers in a line are separated by a space.

Output Specification:

Print in a line all the indices of queries which correspond to "NOT a topological order". The indices start from zero. All the numbers are separated by a space, and there must no extra space at the beginning or the end of the line. It is graranteed that there is at least one answer.

Sample Input:

6 8
1 2
1 3
5 2
5 4
2 3
2 6
3 4
6 4
5
1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6

Sample Output:

3 4

Keys:

• 图的存储和遍历
• 拓扑排序（Topological Order）

Attention:

• 性质：若图顶点按照拓扑排序重新编号，则存储矩阵为上三角阵；
• 由性质可以推断出，若存储图的矩阵为三角阵，则存在拓扑排序，反之不一定成立；
• 拓扑排序算法本身比较简单，了解概念之后自然就可以写出了~

Code:

 /*
 Data: 2019-05-19 20:41:28
 Problem: PAT_A1146#Topological Order
 AC: 22:04

 题目大意：
 判别拓扑排序
 输入：
 第一行给出顶点数N<=1e3，和边数M<=1e4
 接下来M行，给出顶点及其有向边（顶点从1~N）
 接下来给出查询次数K
 接下来K行给出顶点序列
 输出：
 按序号给出不是拓扑排序的序列（0~K-1）
 */

 #include<cstdio>
 #include<algorithm>
 #include<vector>
 using namespace std;
 const int M=1e3+;
 vector<int> grap[M],id(M),ans;

 int main()
 {
 #ifdef    ONLINE_JUDGE
 #else
     freopen("Test.txt", "r", stdin);
 #endif

     int n,m,u,v,s[M];
     scanf("%d%d", &n,&m);
     fill(id.begin(),id.end(),);
     for(int i=; i<m; i++)
     {
         scanf("%d%d",&v,&u);
         grap[v].push_back(u);
         id[u]++;
     }
     scanf("%d", &m);
     for(int i=; i<m; i++)
     {
         vector<int> d = id;
         for(int j=; j<n; j++)
             scanf("%d", &s[j]);
         for(int j=; j<n; j++)
         {
             v=s[j];
             if(d[v]==)
                 for(int k=; k<grap[v].size(); k++)
                     d[grap[v][k]]--;
             else
             {
                 ans.push_back(i);
                 break;
             }
         }
     }
     for(int i=; i<ans.size(); i++)
         printf("%d%c", ans[i],i==ans.size()-?'\n':' ');

     return ;
 }