HDU 4456 Crowd

Crowd

Time Limit: 5000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1287    Accepted Submission(s): 290

Problem Description

City F in the southern China is preparing lanterns festival celebration along the streets to celebrate the festival. 
Since frequent accidents had happened last year when the citizens went out to admire the colorful lanterns, City F is planning to develop a system to calculate the degree of congestion of the intersection of two streets. 
The map of City F is organized in an N×N grid (N north-south streets and N west-east street). For each intersection of streets, we define a density value for the crowd on the intersection. 
Initially, the density value of every intersection is zero. As time goes by, the density values may change frequently. A set of cameras with new graphical recognition technology can calculate the density value of the intersection easily in a short time.
But the administrator of the police office is planning to develop a system to calculate the degree of congestion. For some consideration, they come up with a conception called "k-dimension congestion degree". The "k-dimension congestion degree" of intersection (x0,y0) is represented as "c(x0,y0,k)", and it can be calculated by the formula below:

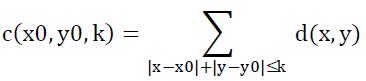
Here, d(x,y) stands for the density value on intersection (x,y) and (x,y) must be in the N×N grid. The formula means that all the intersections in the range of manhattan distance k from (x0,y0) effect the k-dimension congestion degree of (x0,y0) equally, so we just simply sum them up to get the k-dimension congestion degree of (x0,y0). 
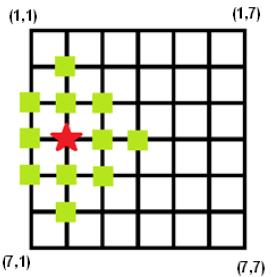
The figure below shows a 7×7 grid, and it shows that if you want to get the 2-dimension congestion degree of intersection (4,2),you should sum up the density values of all marked intersections.

 

Input

These are multiple test cases. 
Each test case begins with a line with two integers N, M, meaning that the city is an N×N grid and there will be M queries or events as time goes by. (1 ≤ N ≤10 000, 1 ≤ M ≤ 80 000) Then M lines follow. Each line indicates a query or an event which is given in form of (p, x, y, z), here p = 1 or 2, 1 ≤ x ≤ N, 1 ≤ y ≤ N. 
The meaning of different p is shown below.
1. p = 1 the value of d(x,y) is increased by z, here -100 ≤ z ≤ 100.
2. p = 2 query the value of c(x,y,z), here 0 ≤ z ≤ 2N-1.
Input is terminated by N=0.

 

Output

For each query, output the value for c(x,y,z) in a line.

 

Sample Input

8 5

1 8 8 1

1 1 1 -2

2 5 5 6

1 5 5 3

2 2 3 9

3 2

1 3 2 -9

2 3 2 0

0

 

Sample Output

1

1

-9

 

Source

2012 Asia Hangzhou Regional Contest

 

解题：隔壁老王对我说，这个曼哈顿距离啊覆盖的区域旋转45度后就是一个矩形区域，既然是矩形区域，范围还那么大，其实可以更大的，只是内存真抠门。。。

 

上吧，CDQ

 

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 const int maxn = ;
 struct QU {
     int x1,x2,y,id,f;
     QU(int a = ,int b = ,int c = ,int d = ,int e = ) {
         x1 = a;
         x2 = b;
         y = c;
         id = d;
         f = e;
     }
     bool operator<(const QU &t)const {
         return y < t.y;
     }
 } Q[maxn],A[maxn],B[maxn];
 LL C[maxn],ans[maxn];
 void add(int i,int val) {
     while(i < maxn) {
         C[i] += val;
         i += i&-i;
     }
 }
 LL sum(int i,LL ret = ) {
     while(i > ) {
         ret += C[i];
         i -= i&-i;
     }
     return ret;
 }
 void cdq(int L,int R) {
     if(R <= L) return;
     int mid = (L + R)>>;
     cdq(L,mid);
     cdq(mid+,R);
     int a = ,b = ,j = ;
     for(int i = L; i <= mid; ++i)
         if(Q[i].id == -) A[a++] = Q[i];
     for(int i = mid + ; i <= R; ++i)
         if(Q[i].id != -) B[b++] = Q[i];
     sort(A,A + a);
     sort(B,B + b);
     for(int i = ; i < b; ++i) {
         for(; j < a && A[j].y <= B[i].y; ++j) add(A[j].x1,A[j].f);
         ans[B[i].id] += B[i].f*sum(B[i].x2);
         ans[B[i].id] -= B[i].f*sum(B[i].x1);
     }
     for(int i = ; i < j; ++i) add(A[i].x1,-A[i].f);
 }
 int main() {
     int n,m,op,x,y,z,tot,ask;
     while(scanf("%d",&n),n) {
         scanf("%d",&m);
         ask = tot = ;
         memset(ans,,sizeof ans);
         while(m--) {
             scanf("%d%d%d%d",&op,&x,&y,&z);
             if(op == ) Q[tot++] = QU(x + y,,y - x,-,z);
             else {
                 int cx = x + y;
                 int cy = y - x;
                 int x1 = cx - z;
                 int x2 = cx + z;
                 int y1 = cy - z;
                 int y2 = cy + z;
                 Q[tot++] = QU(x1-,x2,y2,ask,);
                 Q[tot++] = QU(x1-,x2,y1-,ask++,-);
             }
         }
         cdq(,tot-);
         for(int i = ; i < ask; ++i)
             printf("%I64d\n",ans[i]);
     }
     return ;
 }