TensorFlow-正弦函数拟合

　　MNIST的代码还是有点复杂，一大半内容全在搞数据，看了半天全是一滩烂泥。最关键的是最后输出就是一个accuracy，我根本就不关心你准确率是0.98还是0.99好吗？我就想看到我手写一个5，你程序给我输出一个5，就这么简单。

　　粗略看了文档和网上找了些资料，感觉上吧，倒是有点像Verilog。描述图结构的时候每句话定义一个tensor，它的值由tensorflow下的某一个函数以之前定义过的tensor作为参数运算得到的结果。

　　参考了一下别人的代码，自己写了一个比较直观，能马上看到结果的图，功能是拟合正弦函数。

import tensorflow as tf
import math

#输入层
xs = tf.placeholder(tf.float32,[None,1],name="xs")
ys = tf.placeholder(tf.float32,[None,1],name="ys")

#隐藏层
W1 = tf.Variable(tf.random_normal([1,15]))
b1 = tf.Variable(tf.zeros([1,15])+0.1)
Wx_plus_b1 = tf.matmul(xs,W1) + b1
output1 = tf.nn.relu(Wx_plus_b1)

#输出层
W2 = tf.Variable(tf.random_normal([15,1]))
b2 = tf.Variable(tf.zeros([1,1])+0.1)
Wx_plus_b2 = tf.matmul(output1,W2) + b2
output2 = tf.add(Wx_plus_b2,0,name="output")
#损失
loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys-output2),reduction_indices=[1]))
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(loss)
#初始化
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

#训练
def loop_i():
    ret=-1*math.pi;
    for i in range(200):
        yield ret
        ret+=math.pi/100
for j in range(1000):
    i_range = loop_i();
    for i in i_range:
        _,loss_value = sess.run([train_step,loss],feed_dict={xs:[[i]],ys:[[math.sin(i)]]}) #进行梯度下降运算，并计算每一步的损失
    if(j%50==0):
        print(loss_value)
#保存
saver = tf.train.Saver()
save_path = saver.save(sess,"E:/python/model")

　　图就是一个简单的1->15->1的全连接，比较好理解。不过在模型的保存和导出这里遇到了很大的困扰，场面一度十分尴尬，还好最后搞定了。

　　保存是这样保存的：

saver = tf.train.Saver()
save_path = saver.save(sess,"E:/python/model")

　　然后目录下生成四个文件

　　

　　需要恢复的时候先导入图结构：

saver = tf.train.import_meta_graph('E:/python/model.meta')
graph = tf.get_default_graph()

　　获取需要发生交互的tensor，比如输入输出点：

xs=graph.get_tensor_by_name('xs:0')
ys=graph.get_tensor_by_name('ys:0')
output=graph.get_tensor_by_name('output:0')

　　这里的name是在保存之前定义好的，比如这里：

　　

　　根据目前的了解，想加name貌似必须是xxx=tf.xxxxxx(xxxxxxxx, name="")这种形式，所以上面的代码里被迫写了一句这种搞笑定义。

　　接下来恢复之前计算好的数值：

saver.restore(sess, tf.train.latest_checkpoint('E:/python'))

　　函数里的参数是模型文件所在的目录，而不是文件本身。

　　测试的代码：

import tensorflow as tf
#导入图结构
saver = tf.train.import_meta_graph('E:/python/model.meta')
graph = tf.get_default_graph()
xs=graph.get_tensor_by_name('xs:0')
ys=graph.get_tensor_by_name('ys:0')
output=graph.get_tensor_by_name('output:0')

with tf.Session() as sess:
    #恢复变量
    saver.restore(sess, tf.train.latest_checkpoint('E:/python'))
    #测试
    test = sess.run(output, feed_dict={xs: [[1]], ys: [[0]]})
    print(test)

　　输出结果：

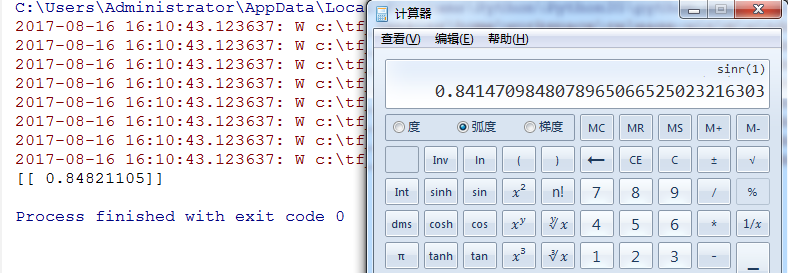
　　前两位正确，还可以接受。