浅谈RMQ问题

RMQ:question

有一个长度为

N

N

N的数组，数组中的数是无序的（

1

<

=

n

<

=

5

∗

1

0

5

1<=n<=5*10^5

1<=n<=5∗105）。
给定

Q

Q

Q次查询，每次给出一个区间

[

L

,

R

]

[L,R]

[L,R]，问区间最值是多少。

Q

Q

Q为

3

×

1

0

6

3×10^6

3×106

浅浅地分析下？

我们拿到题的第一感觉？

• 肯定是暴力枚举
• 不做任何处理，直接查询（这谁都会吧）
• O

  (

  Q

  ∗

  n

  2

  )

  O(Q*n^2)

  O(Q∗n2),时间难以承受

思考下，暴力储存？

• 因为这是区间问题，考虑区间dp？
• F

  [

  i

  ]

  [

  j

  ]

  表示区间

  [

  i

  ,

  j

  ]

  内的最值

  F[i][j]表示区间[i,j]内的最值

  F[i][j]表示区间[i,j]内的最值

• 处理：

  O

  (

  n

  3

  )

  O(n^3)

  O(n3)，查询:

  O

  (

  1

  )

  O(1)

  O(1),比上个好了点，但是还是无法承受。

进一步思考？

• 我们上一个方案的状态转移方程是什么？
• F

  [

  i

  ]

  [

  j

  ]

  =

  m

  a

  x

  (

  f

  [

  i

  ]

  [

  k

  ]

  ,

  f

  [

  k

  +

  1

  ]

  [

  j

  ]

  )

  (

  i

  <

  =

  k

  <

  =

  j

  )

  不需要循环枚举

  F[i][j]=max(f[i][k],f[k+1][j])(i<=k<=j)不需要循环枚举

  F[i][j]=max(f[i][k],f[k+1][j])(i<=k<=j)不需要循环枚举

• 所以，我们真的需要那么多空间吗？
• 于是，我们可以将

  F

  F

  F数组的含义变为

• F

  [

  i

  ]

  [

  k

  ]

  表示区间

  [

  i

  ,

  i

  +

  k

  −

  1

  ]

  的最值

  F[i][k]表示区间[i,i+k-1]的最值

  F[i][k]表示区间[i,i+k−1]的最值

• 这样依旧会爆，但是这是我们迈出成功地一大步

最终？

• 这个时候，就有一个很厉害的东西： ST表
• 这个是什么呢？请看
• F

  [

  i

  ]

  [

  j

  ]

  表示区间

  [

  i

  ,

  i

  +

  2

  j

  −

  1

  ]

  内的最值

  F[i][j]表示区间[i,i+2^j-1]内的最值

  F[i][j]表示区间[i,i+2j−1]内的最值

• 这时候，空间就不会爆！
• 转移方程::

  F

  [

  i

  ]

  [

  j

  ]

  =

  m

  a

  x

  (

  F

  [

  i

  ]

  [

  j

  −

  1

  ]

  ,

  F

  [

  i

  ]

  [

  i

  +

  (

  1

  <

  <

  (

  j

  −

  1

  )

  )

  ]

  F[i][j]=max(F[i][j-1],F[i][i+(1<<(j-1))]

  F[i][j]=max(F[i][j−1],F[i][i+(1<<(j−1))]

• <

  <

  是左移，

  1

  <

  <

  j

  =

  2

  j

  <<是左移，1<<j=2^j

  <<是左移，1<<j=2j,其实

  <

  <

  <<

  <<的优先级比

  −

  -

  −低,所以最里面的括号可以删掉

• 最后是:

  F

  [

  i

  ]

  [

  i

  ]

  =

  m

  a

  x

  (

  F

  [

  i

  ]

  [

  j

  −

  1

  ]

  ,

  F

  [

  i

  ]

  [

  i

  +

  (

  1

  <

  <

  j

  −

  1

  )

  ]

  F[i][i]=max(F[i][j-1],F[i][i+(1<<j-1)]

  F[i][i]=max(F[i][j−1],F[i][i+(1<<j−1)]

• 为什么？
• 我举个例子：

  F

  [

  1

  ]

  [

  3

  ]

  F[1][3]

  F[1][3]表示的是

  区间

  [

  1

  ,

  1

  +

  2

  3

  ]

  =

  [

  1

  ,

  8

  ]

  ，

  区间[1,1+2^3]=[1,8]，

  区间[1,1+23]=[1,8]，他就可以从

  区间

  F

  [

  1

  ,

  4

  ]

  和

  F

  [

  5

  ,

  8

  ]

  区间F[1,4]和F[5,8]

  区间F[1,4]和F[5,8]表示

• 怎么查询？
• 我们可以考虑快速幂，比如

  10

  10

  10二进制表示

  1010

  1010

  1010,所以比较大小

  2

  ,

  8

  2,8

  2,8的区间即可

终极优化

• 如果区间大小是31
• 那么我们得连续比较

  16

  ,

  8

  ,

  4

  ,

  2

  ,

  1

  16,8,4,2,1

  16,8,4,2,1的区间

• 复杂度可以接受，但是我们可以继续优化时间复杂度
• 
• 这张图片告诉我们什么道理？
• 比较区间是可以重叠的！！
• 那么我们这需要求出

  l

  o

  g

  2

  n

  {log_{2}}^{n}

  log2​n即可

• 比如

  31

  31

  31,我们可以把它拆成

  [

  1

  ,

  16

  ]

  [

  15

  ,

  31

  ]

  [1,16][15,31]

  [1,16][15,31]来比较，如果预先处理好

  l

  o

  g

  2

  n

  {log_{2}}^{n}

  log2​n我们就可以以

  O

  (

  1

  )

  O(1)

  O(1)的复杂度查询！

怎么预先处理

l

o

g

2

n

{log_{2}}^{n}

log2​n

• 有个代码可以比

  c

  m

  a

  t

  h

  cmath

  cmath的函数快很多

C

o

d

e

:

Code:

Code:

for(int i=1;i<=n;++i)
	lg[i]=lg[i-1]+((1<<lg[i-1])==i);

• 但是这里有个

  B

  U

  G

  BUG

  BUG！如果你要求

  l

  o

  g

  2

  n

  {log_{2}}^{n}

  log2​n,你需要减一

C

o

d

e

Code

Code(我自己写的模板)

#include<bits/stdc++.h>

using namespace std;
int n,m,dp[2][2000005],lo[2000005],a[2000005];
void log_2(){//求log2 n
	for(int i=1;i<=n;i++)
		lo[i]+=lo[i-1]+((1<<lo[i-1])==i);
}
int main()
{
	cin>>n>>m;
	log_2();
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;(1<<i)<=n;i++)
		for(int j=1;j+(1<<i)-1<=n;j++)
			dp[i][j]=1e9;
	for(int i=1;i<=n;i++) dp[0][i]=a[i];
	//初始化rmq，区间dp
	for(int i=1;(1<<i)<=n;i++)
		for(int j=1;j+(1<<i)-1<=n;j++)
			dp[i][j]=min(dp[i-1][j],dp[i-1][j+(1<<i-1)]);
	//查询
	cout<<0<<endl;//题目所需QWQ
	for(int w=2;w<=n;w++){
		int j=w-m,i=w-1;
		if(j<=0) j=1;
		int k=lo[i-j+1]-1;//注意减一
		cout<<min(dp[k][j],dp[k][i-(1<<k)+1])<<endl;
	}
	return 0;
}

注明

我这个代码是基于P1440 求m区间内的最小值的80分代码，因为本蒟蒻太蒟了，不会滚动数组，大家可以拿这道题练练手

关于这道题：
（老师提醒）

因为这题的区间长度只有m，所以可以用滚动数组，减小空间复杂度，不MLE

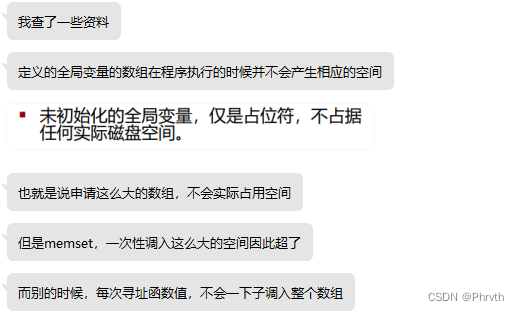
(自己提醒)

不要用memset！不要用memset！用了直接全部MLE，因为