【机器学习基础】——另一个视角解释SVM

SVM的另一种解释

前面已经较为详细地对SVM进行了推导，前面有提到SVM可以利用梯度下降来进行求解，但并未进行详细的解释，本节主要从另一个视角对SVM进行解释，首先先回顾之前有关SVM的有关内容，然后从机器学习的三步走的角度去对SVM进行一个解释。

那么对于传统的机器学习，每个方法最大区别就是损失函数的选取，因此SVM可以看成是另一种损失函数的方法，这种损失函数就是Hinge Loss。另外SVM另一个特点就是使用了Kenel trick。

0. SVM内容回顾

前面说了SVM（主要是二分类）是希望找一个分离超平面，能够将数据分开，使得距离分离超平面最近的点的距离越远越好。

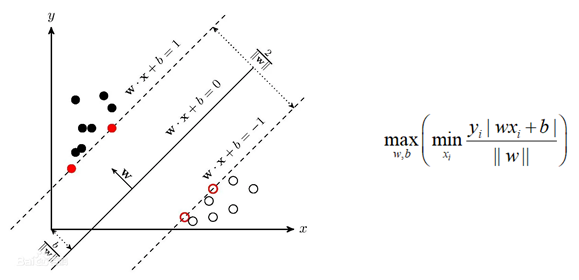
根据优化目标，优化函数变成：

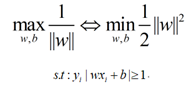
为了使得模型更具有鲁棒性和泛化能力，引入一个松弛变量ξ：

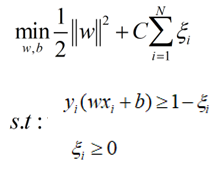
然后就是对这个问题进行求解，主要求解方法就是多目标优化算法，引入拉格朗日因子α，问题转化为求解α，然后最终利用SMO算法求解的过程。

因为前面已有这部分内容，这里就不再赘述了。

下面就是从机器学习通用的方法来解释SVM算法。

1. SVM的另一种解释

  在前面机器学习中，我们采用三步走：1、找一个function set，2、找一个衡量function好坏的loss function；3、根据loss function找出一个best function。

   也就是我们希望找一个g(x)，使得输入x使得正类样本输出大于0，负类样本输出小于0。那么对于loss function，最理想的情况下，当g(x)=y时，loss=0，当g(x)≠y时，loss=1。但通常δ(g(x)=y)这种loss是不可微的，因此这里loss function都用l(f(x),y)来表示。通过minimize l(f(x),y)来进行优化求解。具体地loss function也有多种，下面具体看几个（这里分类正类为1，负类为-1）：

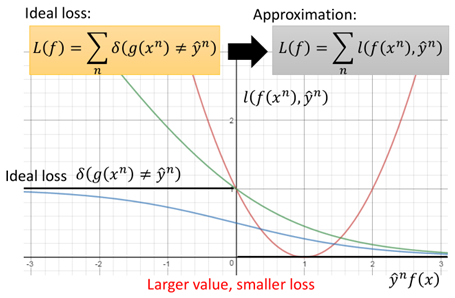
上图中一共有四种loss function：

①：Ideal loss，就是图中黑色的那条线，就是理想下的loss function，即当y=1，f(x)>0或y=-1，f(x)<0时loss为0，当二者不同号时loss为1。

②：square loss：也就是图中红色的线，其方程形式如下：

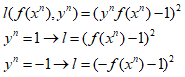
从图中则可以看出，当y与f(x)不同号时，没问题，则会有个loss，而当y与f(x)相乘很大时，也会产生一个很大的loss。这也就证明了为什么在分类时不能使用square loss这样的损失函数。

③：sigmoid + square loss：也就是图中蓝色的那条线，其方程形式如下：

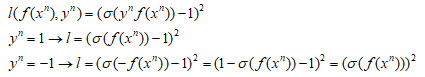
图中可以看出当y与f(x)不同号时，当这个负数很小时，loss并没有继续增加，同样的当y与f(x)相乘很大时，同样还是有一个比较小的loss。在LR算法中提到过，通常不使用square loss，可能效果不好，这里可以更容易理解。在LR中往往使用的sigmoid + crossentropy。

④：sigmoid+crossentropy : 就是图中绿色的那条线，其方程形式及推导如下：

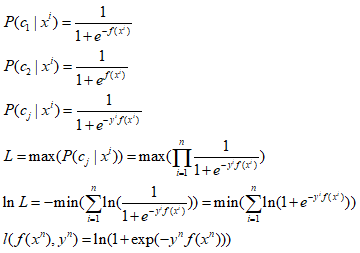
图中可以看出这个在y与f(x)不同号时，也就是目标值与真实值差距越大，损失也就越大，当y与f(x)相乘很大时，loss是趋于0。因此在分类中更多的是使用crossentropy损失。

  而在SVM中，损失函数使用的则是Hinge Loss损失函数，其函数如图所示：

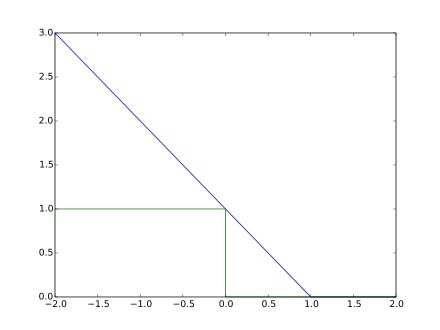
Hinge Loss的函数方程为：

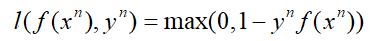
把Hinge Loss与上面的那些损失函数画在一起进行一个对比：

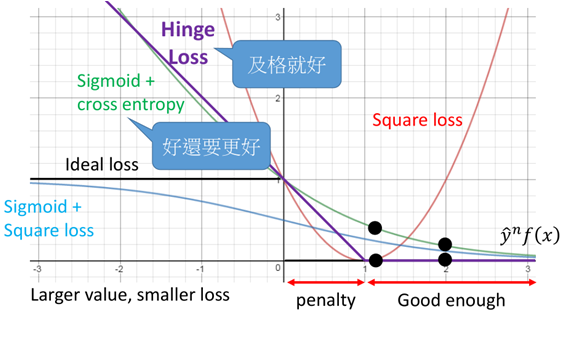
图中可以看出，当y与f(x)同号时，且足够大，则loss=0，而在0~1之间时依然会有一定的损失，而当二者不同号时，loss则持续增大。

相比于cross entropy而言，在二者不同号时，二者基本相似，但是当二者同号，且足够大时，当大于1时，Hinge loss表现为已经足够了，不需要再优化了，而对于crossentropy，尽管已经做的很好了，但还是存在一定的loss，还要做的更好。这可能会导致模型的过拟合，因此SVM模型具有更强的泛化能力。

搞定了loss function之后，那么SVM算法的三个步骤如下:

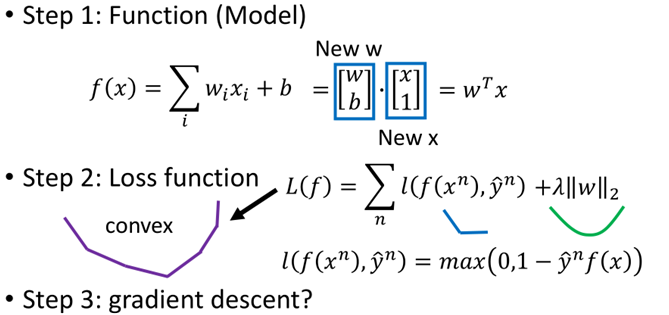
第一步就是一个超平面的集合，这里将b合并进w中；

第二步就是一个Hinge loss，然后加上一个正则化项，两个凸函数相加仍然是个凸函数；

第三步就是直接利用梯度下降进行求解，这里虽然hinge loss存在不可导点，但是并非数据刚好落在不可导的地方，类似于maxpool中的求导。具体求导如下：

至此，SVM另一个角度进行解释和求解已经完成了，下面我们把这种形式的SVM与传统的SVM进行一个比较：

这里令：

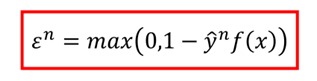
那么损失函数可以写成：

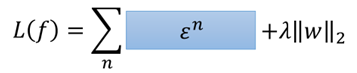
而对于ε这个东西，它与下面这两个式子：

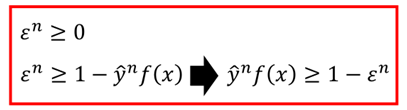
原本二者不是等价的，因为上面的方框是一个确定的值，而下面的方框则表示的是一个范围，但是当加上minimize之后，两个红色的框上的内容就是等价的。

经过变形yf(x)>1-ε，那么ε就是松弛变量。

2.SVM中的核方法

在说核方法之前，首先是上面问题的求解，在进行梯度下降求解之后，可以得到：

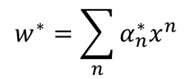
这就是SVM的对偶问题，将求w最后转化为求α得问题上。而对于上面这个式子，在传统SVM中，使用的是拉格朗日求极值的方法，从而得到SVM的对偶问题，这里我们利用梯度下降：

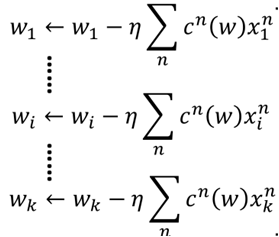
假设初始化w1=0(矩阵)，那么，最终w则为：

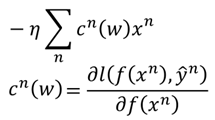
这里c(w)里有很多是0的项，因为一部分的求导为0，因此，w*最后就是最开始那个式子，最终问题就变成求解α了，具体求解方法前面SMO算法已经说过，这里就不再说了。

那些不为0的α就是所谓的“支持向量”，这里也能更好地理解什么是支持向量。

然后，w就可以写成下面这样的形式：

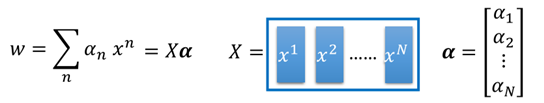
再带回原方程中f(x)中，则有：

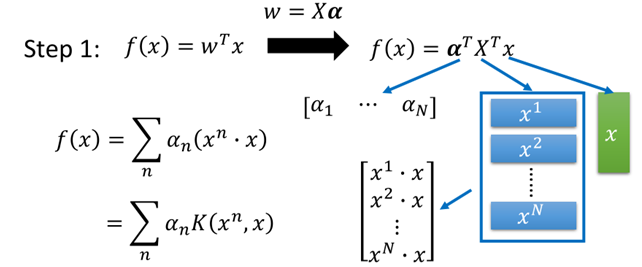
最终f(x)变成了所需要使用核方法的形式：

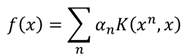
同时，要找一组α={α1，α2，......，αn}，使得损失函数L最小：

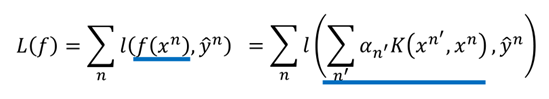
在核技巧中我们并不需要知道x和xn（在高维空间中）是什么，只需要知道K(xn,x)的值就可以。

直接计算K(x,z)往往比先映射到高维空间再进行内积计算快的多，举个例子：

有一个x=[x1,x2]，z=[z1,z2]，我们进行转换，假设先转换成高维空间中的φ(x)，φ(z)，再相乘：

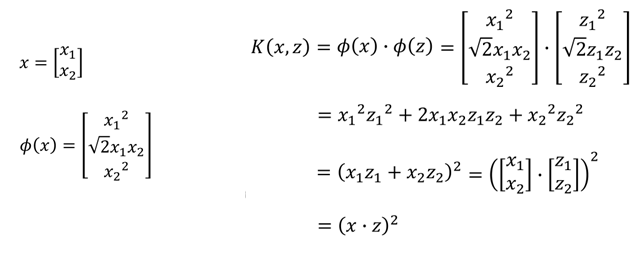
最终可以看到结果和直接进行相乘是一样的。

假设核函数为tanh函数，那么就有：

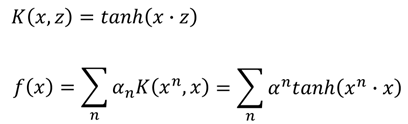
而当核函数是sigmoid函数的时候，那么此时SVM则可以看成是有一层隐藏层的神经网络：

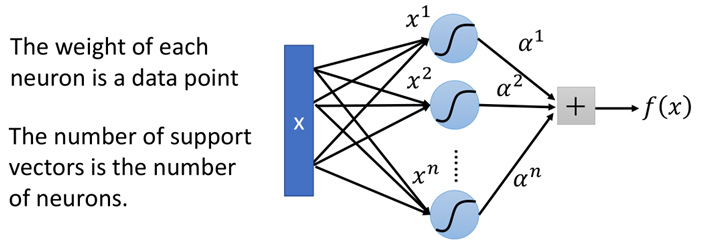
该网络中神经元的个数就是支持向量的个数，而每个权重就是对应的样本点。

3.小结

上面就是从原始机器学习的角度去看待SVM，从原来求解QP问题的方法转变为梯度下降的方法，但最终落脚还是要继续求解α这样一个问题上。SVM最重要的两个特点一个是使用了Hinge Loss另一个就是核方法，而核方法在LR中也可以使用，但是由于SVM在进行分类时，只考虑支持向量，因此进行计算时相对较为快速，而LR是所有点参与计算，如果使用核方法则在高维空间中运算量过大，导致效率低，因此LR通常不采用核技巧。此外，相比于LR分类算法而言，SVM更具有鲁棒性。