聪明的暴力枚举求abcde/fghij=n

目录

• 前言
• 一、题目
• 二、暴力初解
• 三、优化再解（借鉴bitmap）
• 总结

前言

枚举如何聪明的枚举？那就是优化啦！下面梳理之前做过的一个暴力枚举的题，想了蛮久最后把它优化了感觉还不错，算是比较聪明的枚举了。

一、题目

输入正整数n，输出所有如abcde/fghij=n的表达式，其中a-j为数字0-9的不重复的排列，这里的除为整除，请统计这样的组合一共有多少个？例如：

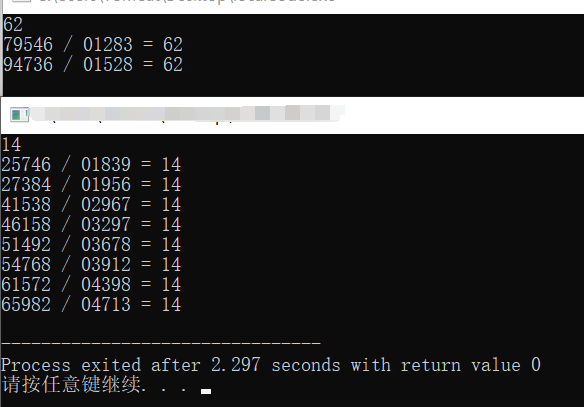
输入：62

输出：

79546/01283=62

94736/01528=62

二、暴力初解

初解思路：

直接调的全排列函数，枚举所有的可能然后判断所有的结果，可以就输出

#include <bits/stdc++.h>
using namespace std;
int main(){
	int a[10]={0,1,2,3,4,5,6,7,8,9};
	int n; cin>>n; int num=0;
	do{
		int x =a[0]*10000+a[1]*1000+a[2]*100+a[3]*10+a[4];
		int y =a[5]*10000+a[6]*1000+a[7]*100+a[8]*10+a[9];
		if(x==y*n){
			cout<<a[0]<<a[1]<<a[2]<<a[3]<<a[4]<<"/"<<a[5]<<a[6]<<a[7]<<a[8]<<a[9]<<"="<<n<<endl;
		}
	}while(next_permutation(a,a+10));
	return 0;
}

三、优化再解（借鉴bitmap）

bitmap简介：https://www.cnblogs.com/cjsblog/p/11613708.html

再解思路：

欲求abcde / fghij = n的表达式，

从1234枚举到98765即可，设i 为 abcde，那么fghij = n * i，

这样问题就转化成了判断 i 和 n * i 一起是否数字为0-9的组合，

然后借鉴bitmap的思路用10位二进制数表示0-9这10个数字，遍历 i 和 n * i 的位数，如果存在0-9就把对应位的1转为0，最后计算完后如果是所有数字都不相同的话就是0；

#include<bits/stdc++.h>
using namespace std;

int judge(int a , int b)//判断a,b所有数字是否都不相同，且为0-9
{
	int allNum=1023;//所有二进制数为1，一共10个1，也就是1024-1；
	string str = to_string(a)+to_string(b);//合在一起运算
	if(a<10000 || b<10000) str+='0';//避免缺少了一个0的计算
	for(char i : str){
		int tmp=1;
		for(int j = (i-'0');j>0;j--)//把1移到对应的位
			tmp=tmp<<1;
		allNum&=(~tmp);//这里allNum-=tmp;也可以
	}
	return allNum;//如果a,b所有数字都不相同且为0-9那么返回0，否则返回非0;
}

int main() {
	int n=0;
    scanf("%d" , & n);
    for(int i = 1234 ; i * n < 98766 ; i ++) {
        if(!judge(i, i * n))//如果非0则不能输出所以取反跳过，如果是0那么可以输出所以取反输出可行解
            printf("%05d / %05d = %d\n",i*n,i,n);
    }
    return 0;
}

总结

如果枚举0~9的所有排列，需要10！=3628800次！，可以接受，但是没有必要；聪明的枚举比如输入62只需要359次即可！这算是比较聪明的枚举了吧，如果有问题欢迎评论指出，本人也是算法菜鸡一枚。