OpenFOAM 编程 | 求解捕食者与被捕食者模型（predator-prey model）问题（ODEs）

0. 写在前面

本文问题参考自文献 $^{[1]}$ 第一章例 6，并假设了一些条件，基于 OpenFOAM-v2206 编写程序数值上求解该问题。笔者之前也写过基于 OpenFOAM 求解偏分方程的帖子，OpenFOAM 编程 | One-Dimensional Transient Heat Conduction。

1. 问题描述

假设一群山猫（捕食者）和一群山兔（被捕食者）生活在同一片区域，那么我们可以知道，山猫吃了山兔，繁殖力会增强，山猫的数量会增加。这样一来，山兔的数量会随之减少。接下来，山猫由于食物短缺而数量减少，进而导致山兔遇到山猫的机会减少（被吃掉的概率降低），结果山兔的数量又逐渐增加，这样山猫得到食物的机会也随之增加，其数量又再一次增加，而山兔的数量又会再一次随之减少，如此不断循环。

2. 解析求解

设任意 $t$ 时刻山兔与山猫的数量分别是 $\phi$ 和 $\psi$ ，二者的变化服从下面动力学方程

\[\begin{aligned}
\frac{\mathrm{d}\phi}{\mathrm{d}t} &= k_1 \phi - \mu\phi\psi \\
\frac{\mathrm{d}\psi}{\mathrm{d}t} &= \nu\phi\psi - k_2 \psi
\end{aligned}
\tag1
\]

其中，$k_1$，$k_2$，$\mu$ 和 $\nu$ 都是正常数。

在上述方程中有几点需要注意：

$k_1\phi$ 表示山兔种群的净增长率，与山兔种群数量成正比。
$-\mu\phi\psi$ 表示山兔被山猫吃掉而导致的减少率，与乘积 $\phi\psi$ （可表示两种动物的相遇概率）成正比。
$\nu\phi\psi$ 表示山猫种群的增长率，由于其数量增长取决于捕食（相遇才有可能），因此 $\nu$ 为正值。
$-k_2\psi$ 表示山猫种群的死亡率，与其种群数量成正比。

方程组（1）因为含有乘积项，因此是非线性的。现采用线性化的特殊方法求解，即研究种群数量 $\phi$ 和 $\psi$ 在其稳定值附近的微小涨落。设方程组（1）的稳态解为 $\phi=\phi_0$，$\psi=\psi_0$，它们由下面条件决定

\[\begin{aligned}
\left . \frac{\mathrm{d}\phi}{\mathrm{d}t} \right |_{\phi=\phi_0,\psi=\psi_0} &= 0 \\
\left . \frac{\mathrm{d}\psi}{\mathrm{d}t} \right |_{\phi=\phi_0,\psi=\psi_0} &=0
\end{aligned}
\]

也就是

\[\begin{aligned}
k_1 \phi_0 - \mu\phi_0\psi_0 &= 0 \\
\nu\phi_0\psi_0 - k_2 \psi_0 &=0
\end{aligned}
\tag2
\]

代数方程（2）的解为

\[\begin{aligned}
\phi_0 &= \frac{k_2}{\nu} \\
\psi_0 &=\frac{k_1}{\mu}
\end{aligned}
\]

现在，将方程组（1）的解写为下面形式

\[\begin{aligned}
\phi &= \phi_0+ \xi \\
\psi &= \psi_0 + \eta
\end{aligned}
\]

其中，$\xi$ 和 $\eta$ 与 $\phi_0$ 和 $\psi_0$ 相比都是小量。将上述解带入方程组（1）中可以得到关于变量 $\xi$ 和 $\eta$ 的方程组

\[\begin{aligned}
\frac{\mathrm{d}\xi}{\mathrm{d}t} &= k_1\xi-\mu\phi_0\eta-\mu\psi_0\xi-\mu\xi\eta\\
\frac{\mathrm{d}\eta}{\mathrm{d}t} &= \nu\phi_0\eta + \nu\psi_0\xi - k_2\eta+\nu\xi\eta
\end{aligned}
\tag3
\]

其中非线性项 $\mu\xi\eta$ 和 $\nu\xi\eta$ 为二阶小量，可以忽略；再将稳态解代入可得线性化的耦合方程组

\[\begin{aligned}
\frac{\mathrm{d}\xi}{\mathrm{d}t} &= -k_2\frac{\mu}{\nu}\eta\\
\frac{\mathrm{d}\eta}{\mathrm{d}t} &= k_1\frac{\nu}{\mu}\xi
\end{aligned}
\]

解耦后可得到

\[\begin{aligned}
\frac{\mathrm{d}^2\xi}{\mathrm{d}t^2} +k_1k_2\xi&= 0\\
\frac{\mathrm{d}^2\eta}{\mathrm{d}t^2} +k_1k_2\eta&= 0
\end{aligned}
\tag4
\]

可以知道，式（4）与 L-C 震荡电路及单摆问题同属于相同的数学模型

\[\frac{\mathrm{d}^2y}{\mathrm{d}t^2} + k^2 y = 0
\]

其通解为

\[y(t) = E\sin(kt+\delta)\ \ \ \ 或\ \ \ \ y(t) = E\cos(kt+\delta)
\]

其中，$E$ 和 $\delta$ 为振幅和初相位，与具体问题有关。

那么我们也可以得到本问题的最终解的形式为

\[\begin{aligned}
\phi &= \frac{k_2}{\nu} + E_1 \sin\left(\sqrt{k_1k_2}t+\delta_1\right)\\
\psi &= \frac{k_1}{\mu} +E_2 \sin\left(\sqrt{k_1k_2}t+\delta_2\right) \\
\end{aligned}
\]

其中，每个公式中振幅与初相位取决于各自的初始条件。

3. 数值求解

从上一节可知，我们需要数值求解一个耦合的常微分方程组，可以用RungeKutta法$^{[2]}$。简单推导过程如下：

\[\begin{aligned}
\frac{\mathrm{d}\phi}{\mathrm{d}t} &= f_1\left( \phi,\psi \right) \\
\frac{\mathrm{d}\psi}{\mathrm{d}t} &= f_2\left( \phi,\psi \right) \\
\end{aligned}
\]

其中，

\[\begin{aligned}
f_1\left( \phi,\psi \right) &= k_1 \phi - \mu\phi\psi \\
f_2\left( \phi,\psi \right) &= \nu\phi\psi - k_2 \psi \\
\end{aligned}
\]

四阶Runge-Kutta方法可以表示为：

\[\begin{aligned}
\phi^{k+1} &= \phi^{k} + \frac{\Delta t}{6} \left( f_{11} + 2f_{12} + 2f_{13} + f_{14} \right) \\
\psi^{k+1} &= \psi^{k} + \frac{\Delta t}{6} \left( f_{21} + 2f_{22} + 2f_{23} + f_{24} \right) \\
\end{aligned}
\]

其中，

\[\begin{aligned}
f_{i1} &= f_i \left( \phi_k, \psi_k \right) \\
f_{i2} &= f_i \left( \phi_k+\frac{\Delta t}{2}f_{11}, \psi_k+\frac{\Delta t}{2}f_{21} \right) \\
f_{i3} &= f_i \left( \phi_k+\frac{\Delta t}{2}f_{12}, \psi_k+\frac{\Delta t}{2}f_{22} \right) \\
f_{i4} &= f_i \left( \phi_k+{\Delta t}f_{11}, \psi_k+{\Delta t}f_{21} \right) \\
\end{aligned}
\ \ \ \ i=1,2
\]

求解代码采用 Python 编写，如下所示

#!/usr/bin/python3

# -*- coding:utf-8 -*-

import numpy as np

k1 = 0.7

k2 = 0.5

mu = 0.1

nu = 0.02

def f1(phi,psi):

    return k1*phi-mu*phi*psi

def f2(phi,psi):

    return nu*phi*psi-k2*psi

tStart = 0

tEnd   = 100.0

n      = 100000

deltaT = tEnd / n

halfDeltaT = deltaT / 2.0

Solution = np.ndarray([n+1,2])

Solution[0] = [30,20] 

for i in range(n):

    f11 = f1(Solution[i][0], Solution[i][1])

    f21 = f2(Solution[i][0], Solution[i][1])

    f12 = f1(Solution[i][0] + halfDeltaT * f11, Solution[i][1] + halfDeltaT * f21)

    f22 = f2(Solution[i][0] + halfDeltaT * f11, Solution[i][1] + halfDeltaT * f21)

    f13 = f1(Solution[i][0] + halfDeltaT * f12, Solution[i][1] + halfDeltaT * f22)

    f23 = f2(Solution[i][0] + halfDeltaT * f12, Solution[i][1] + halfDeltaT * f22)

    f14 = f1(Solution[i][0] + deltaT * f11, Solution[i][1] + deltaT * f21)

    f24 = f2(Solution[i][0] + deltaT * f11, Solution[i][1] + deltaT * f21)

    Solution[i+1][0] = Solution[i][0] + deltaT / 6.0 * (f11 + 2*f12 + 2*f13 + f14)

    Solution[i+1][1] = Solution[i][1] + deltaT / 6.0 * (f21 + 2*f22 + 2*f23 + f24)

    print((i+1)*deltaT,Solution[i+1][0],Solution[i+1][1])

4. OpenFOAM 求解

使用OpenFOAM 数值求解常微分方程（组）主要用到 ODESystem.H（构造微分方程系统）和 ODESolver.H（求解器）；此外，在 OpenFOAM 中需要对常微分方程（组）进行整理$^{[3]}$，进而方便编写代码进行求解。

对于任意阶常微分方程可以转化为一系列一阶常微分方程，这个过程称为降阶，一阶常微分方程的个数与原方程的阶数相等（对于耦合常微分方程组，其阶数等于所有方程阶数之和）。对于某个 $n$ 阶常微分方程，可按下面形式降阶

\[y^{(n)}(x) = f \left( x, y^{(0)}, y^{(1)},\ldots,y^{(n-1)} \right)
\]

其中，$n$ 为阶数，$y^{(0)}=y$ 。

进一步，引入符号 $\mathrm{D}$ 对各阶导数重新定义，此过程称为转换

\[\mathrm{D}_j = y^{(j-1)}\ \ \ \ j=1,2,\ldots,n-1
\]

最终，使用新符号重新表达原系统，此过程称为诱导

\[\begin{aligned}
\mathrm{D}'_j &= \mathrm{D}_{j+1} \\
\mathrm{D}'_n = y^{(n)} &= f\left( x, \mathrm{D}_1, \mathrm{D}_2,\ldots,\mathrm{D}_n \right)
\end{aligned}
\]

在 OpenFOAM 中，存在另外一个过程，该过程仅与刚性系统求解器相关，这类求解器需要雅可比矩阵和对自变量的偏导数，即

\[J = \begin{bmatrix}
\frac{\partial \mathrm{D}'_1}{\partial \mathrm{D}_1} & \frac{\partial \mathrm{D}'_1}{\partial \mathrm{D}_2} & \cdots & \frac{\partial \mathrm{D}'_1}{\partial \mathrm{D}_n}\\
\frac{\partial \mathrm{D}'_2}{\partial \mathrm{D}_1} & \frac{\partial \mathrm{D}'_2}{\partial \mathrm{D}_2} & \cdots & \frac{\partial \mathrm{D}'_2}{\partial \mathrm{D}_n}\\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial \mathrm{D}'_n}{\partial \mathrm{D}_1} & \frac{\partial \mathrm{D}'_n}{\partial \mathrm{D}_2} & \cdots & \frac{\partial \mathrm{D}'_n}{\partial \mathrm{D}_n}\\
\end{bmatrix}
\ \ \ \ 和 \ \ \ \
\frac{\partial \mathrm{D}'_1}{\partial x},\frac{\partial \mathrm{D}'_2}{\partial x}, ,\ldots, \frac{\partial \mathrm{D}'_n}{\partial x}
\]

接下来，我们看一下如何实现相关求解代码。首先看一下如何构造方程系统。系统代码需要继承 Foam::ODESystem 抽象类，并且需要全部实现三个方法nEqns()、 derivatives() 和 jacobian()，其中 jacobian() 方法对于非刚性求解器可以将实现置空（空函数体）。

让我们重新回顾一下公式（1），可知 nEqns() 应该返回 2；此外，定义 $Y=[\phi,\psi]^{\mathrm{T}}$ ，公式（1）可整理成如下向量形式

\[\frac{\mathrm{d}Y}{\mathrm{d}t} =
\begin{bmatrix}
k_1 & -\mu\phi \\
\nu\psi & -k_2 \\
\end{bmatrix}
Y
\]

因此，导数可按照公式（1）编写即可，只不过需要注意是向量形式。最后，对应之前的描述的降阶过程，可以知道

\[Y' = f\left( t, Y\right)
\]

进而可以知道， $D_1 = Y, D'_1=Y'$，可得到雅可比矩阵和对自变量的偏导数分别为

\[\frac{\partial \mathrm{D}'_1}{\partial \mathrm{D}_1} = \frac{\partial Y'}{\partial Y} =
\begin{bmatrix}
k_1 & -\mu\phi \\
\nu\psi & -k_2 \\
\end{bmatrix},\ \ \ \
\frac{\partial \mathrm{D}'_1}{\partial t} = 0
\]

需要注意的是，雅可比矩阵只有一个元素 $\frac{\partial \mathrm{D}'_1}{\partial \mathrm{D}_1}$，只不过这个元素是一个块的形式。

具体代码实现如下所示

#include "ODESystem.H"

class ODEs : public Foam::ODESystem

{

public:

    ODEs() {}

    ~ODEs() {}

    // 初始化参数

    ODEs(const Foam::scalar k1, const Foam::scalar mu, const Foam::scalar k2,

         const Foam::scalar nu)

    {

        k1_ = k1;

        mu_ = mu;

        k2_ = k2;

        nu_ = nu;

    }

    // 方程个数

    Foam::label nEqns() const override { return 2; }

    // 求导

    void derivatives(const Foam::scalar x, const Foam::scalarField& y,

                     Foam::scalarField& dydx) const override

    { // 两个未知量存成向量，y[0] -> \phi, y[1] -> \psi

        dydx[0] = k1_ * y[0] - mu_ * y[0] * y[1];

        dydx[1] = nu_ * y[0] * y[1] - k2_ * y[1];

    }

    // 计算符号的雅可比矩阵和关于自变量的导数

    void jacobian(const Foam::scalar x, const Foam::scalarField& y, Foam::scalarField& dfdx,

                  Foam::scalarSquareMatrix& dfdy) const override

    {

        dfdx[0] = 0;

        dfdx[1] = 0;

        dfdy[0][0] = k1_;

        dfdy[0][1] = -mu_ * y[0];

        dfdy[1][0] = nu_ * y[1];

        dfdy[1][1] = -k2_;

    }

private:

    Foam::scalar k1_;

    Foam::scalar mu_;

    Foam::scalar k2_;

    Foam::scalar nu_;

};

对应的，我们实现下主函数

#include <iostream>

#include <memory>

#include "ODESystem.H"

#include "ODESolver.H"

class ODEs : public Foam::ODESystem

{

    // 这里的代码在上边已经介绍，此处省略

};

int main(int argc, char* argv[])

{

    const Foam::scalar startTime = 0.0;         // 开始时间

    const Foam::scalar endTime   = 100.0;       // 结束时间

    const Foam::scalar phi0      = 30;          // 山兔初始值

    const Foam::scalar psi0      = 20;          // 山猫初始值

    const Foam::label n          = 100000;      //

    const Foam::scalar deltaT    = endTime / n; // 步长

    // 系数，参考自文献[4]

    const Foam::scalar k1 = 0.7;

    const Foam::scalar mu = 0.1;

    const Foam::scalar k2 = 0.5;

    const Foam::scalar nu = 0.02;

    // 构造对象

    ODEs odes(k1, mu, k2, nu);

    // 构造求解器，具体使用的算法通过参数传递

    Foam::dictionary dict;

    dict.add("solver", argv[1]);

    Foam::autoPtr<Foam::ODESolver> solver = Foam::ODESolver::New(odes, dict);

    // 初始化一些变量

    Foam::scalar tStart = startTime;

    Foam::scalarField PhiPsi(odes.nEqns()); // 因变量

    PhiPsi[0] = phi0;

    PhiPsi[1] = psi0;

    Foam::scalarField ddt(odes.nEqns()); // 保存导数值

    // 计算过程

    for (Foam::label i = 0; i < n; ++i)

    {

        Foam::scalar dtEst = deltaT / 2;

        Foam::scalar tEnd  = tStart + deltaT;

        //

        odes.derivatives(tStart, PhiPsi, ddt);

        solver->solve(tStart, tEnd, PhiPsi, dtEst);

        //

        tStart = tEnd;

        //

        Foam::Info << tStart << "," << PhiPsi[0] << "," << PhiPsi[1] << Foam::endl;

    }

    return 0;

}

此外，CMakeLists.txt 文件可参考笔者之前的随笔，如 OpenFOAM编程 | Hello OpenFOAM 和 OpenFOAM 编程 | One-Dimensional Transient Heat Conduction，此处不再赘述。

5. 数据分析

笔者通过命令行参数分别采用RKCK45 算法和 seulex 算法（需要用到雅可比矩阵）对该问题进行求解，从下图可见二者求解得到的结果是一致的。

同时运行笔者之前提到的 Python 代码后得到的数值结果与 OpenFOAM 计算结果绘制在同一张图中，二者高度重合。

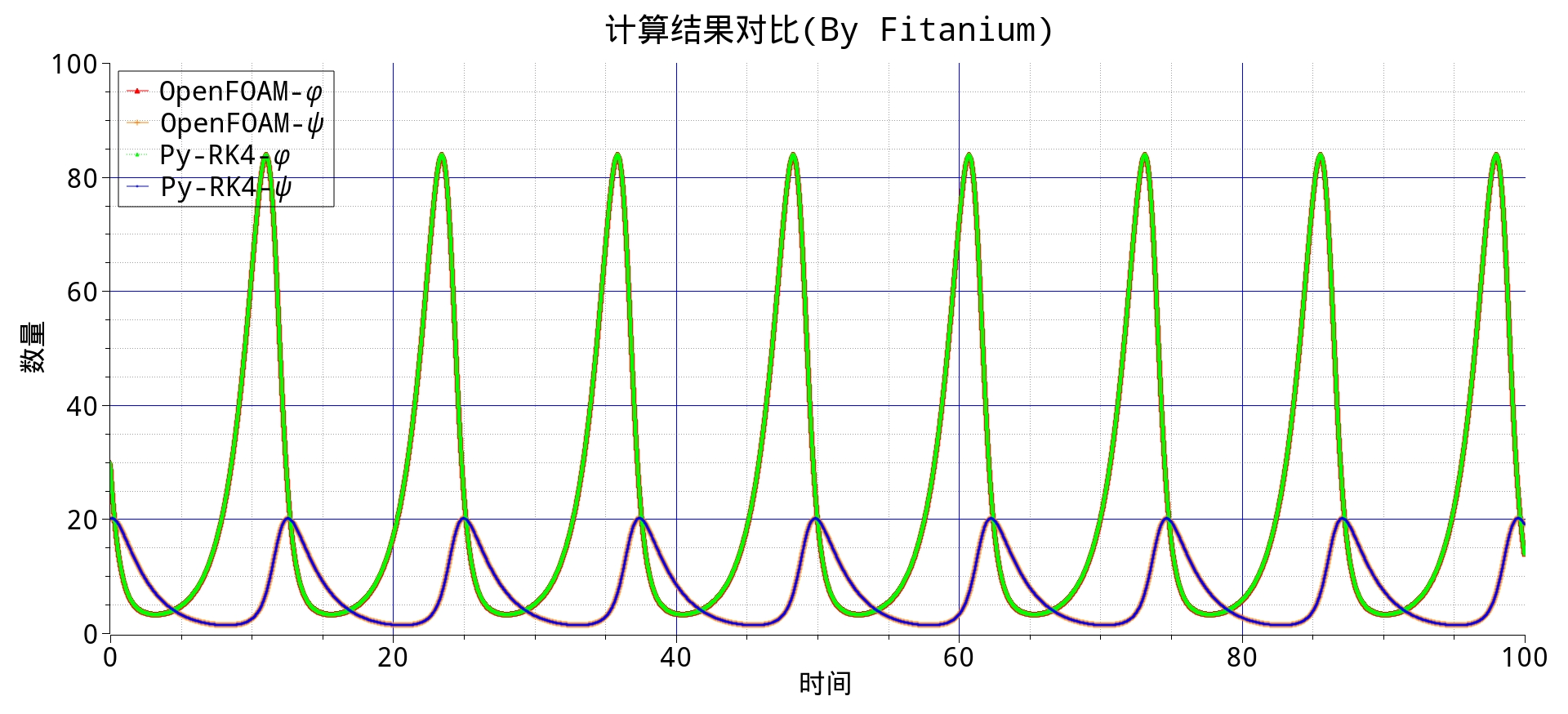
同时，解析解法（线性化的特殊解法）得到的结论是二者均按照 $\sqrt{k_1k_2}$ 圆频率震荡，那么对应的周期为 $T = 2\pi / \sqrt{k_1k_2} = 2 \pi / \sqrt{0.7*0.5} \approx 10.62 $，而数值解中得到的周期为 12.425，笔者认为在本文的条件假设下，其中的差距来自于线性解法中没有考虑非线性，但这个解法仍然具有实际意义。

另外，感兴趣的读者可以尝试使用 Matlab 或 GNU Octave 求解该问题。

参考文献

[1] 顾樵. 数学物理方法[M]. 北京：科学出版社, 2012.

[2] Chenglin LI.数值计算（四十七）RungeKutta求解常微分方程组

[3] Hassan Kassem. How to solve ODE in OpenFOAM

[4] 捕食者与被捕食者模型——logistic-volterra

防止迷路，请关注笔者博客博客园@Fiatanium。

喜欢的朋友还请点赞、收藏、转发，您的支持将是笔者创作的最大动力。