P4047 [JSOI2010]部落划分 方法记录

原题链接

[JSOI2010]部落划分

题目描述

聪聪研究发现，荒岛野人总是过着群居的生活，但是，并不是整个荒岛上的所有野人都属于同一个部落，野人们总是拉帮结派形成属于自己的部落，不同的部落之间则经常发生争斗。只是，这一切都成为谜团了——聪聪根本就不知道部落究竟是如何分布的。

不过好消息是，聪聪得到了一份荒岛的地图。地图上标注了 \(n\) 个野人居住的地点（可以看作是平面上的坐标）。我们知道，同一个部落的野人总是生活在附近。我们把两个部落的距离，定义为部落中距离最近的那两个居住点的距离。聪聪还获得了一个有意义的信息——这些野人总共被分为了 \(k\) 个部落！这真是个好消息。聪聪希望从这些信息里挖掘出所有部落的详细信息。他正在尝试这样一种算法：

对于任意一种部落划分的方法，都能够求出两个部落之间的距离，聪聪希望求出一种部落划分的方法，使靠得最近的两个部落尽可能远离。

例如，下面的左图表示了一个好的划分，而右图则不是。请你编程帮助聪聪解决这个难题。

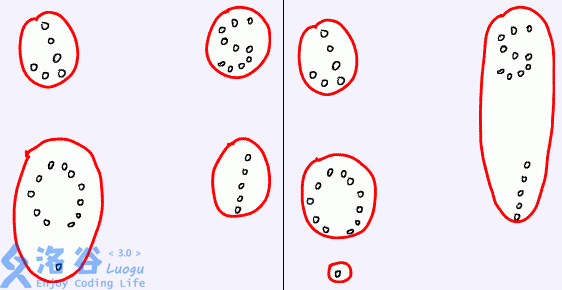
输入格式

输入文件第一行包含两个整数 \(n\) 和 \(k\)，分别代表了野人居住点的数量和部落的数量。

接下来 \(n\) 行，每行包含两个整数 \(x\)，\(y\)，描述了一个居住点的坐标。

输出格式

输出一行一个实数，为最优划分时，最近的两个部落的距离，精确到小数点后两位。

样例 #1

样例输入 #1

4 2
0 0
0 1
1 1
1 0

样例输出 #1

1.00

样例 #2

样例输入 #2

9 3
2 2
2 3
3 2
3 3
3 5
3 6
4 6
6 2
6 3

样例输出 #2

2.00

提示

数据规模与约定

对于 \(100\%\) 的数据，保证 \(2 \leq k \leq n \leq 10^3\)，\(0 \leq x, y \leq 10^4\)。

推荐去看看这篇博客

下面是我的理解（以样例2为例）

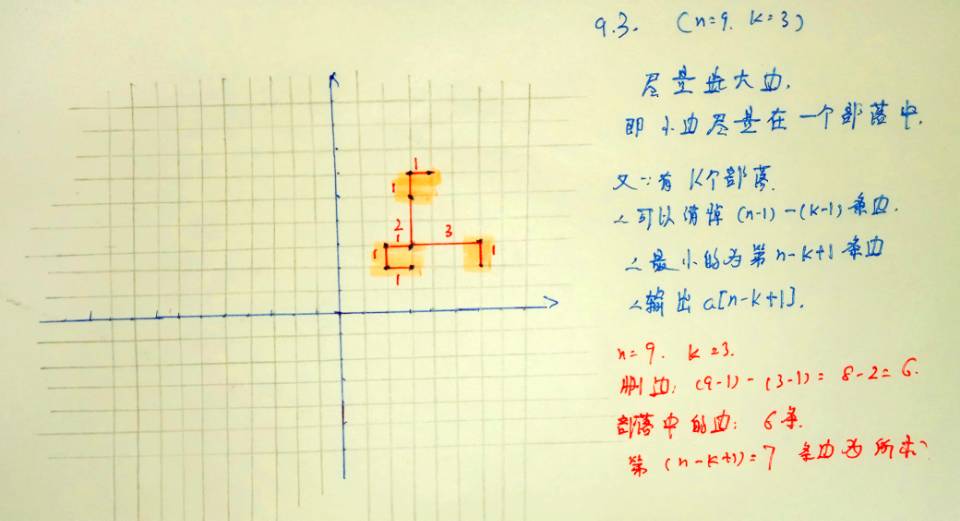
解释

红线描绘出的是“最小生成树”的路径，旁边标的数字为两个居住点之间的路径长度，同一个色块覆盖的为一个部落。（最小生成树的画法不一定唯一，但对答案不影响）

可以看出来这道题使用了贪心的想法：即让小边尽量在一个部落中，让长边暴露在部落覆盖范围外。

且，由题目中“靠得最近的两个部落尽可能远离”可知，应当在最小生成树的基础上进行操作。

又由题知：n个居住点，k个部落，那么部落中的边数=\((n-1)-(k-1)\)。对所有的边从小到大排序，则第\((n-1)-(k-1)+1\)即第\(n-k+1\)条边为首条暴露在部落覆盖范围外的边，即我们所求的“靠得最近的两个部落之间的距离”。

以下为AC代码。为了方便理解，变量名与《算法竞赛进阶指南》P364 Kruskal模板统一。

点击查看代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=1000005;
struct rec
{
	int u,v;
	double dis;
}edge[N];
int fa[N],n,m,cnt;
bool operator < (rec a,rec b)
{
	return a.dis<b.dis;
}
int get(int x)
{
	if(x==fa[x]) return x;
	return fa[x]=get(fa[x]);
}
double a[N];
int x[N],y[N];
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		scanf("%d%d",&x[i],&y[i]);
		fa[i]=i;
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<i;j++)
		{
			cnt++;
			edge[cnt].u=i;
			edge[cnt].v=j;
			edge[cnt].dis=(double)sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));//计算距离
		}
	sort(edge+1,edge+cnt+1);
	int i=1,j=0;
	while(j<n-1)
	{
		int fu=get(edge[i].u);
		int fv=get(edge[i].v);
		double dis=edge[i].dis;
		if(fu!=fv)
		{
			fa[fu]=fv;
			j++;
			a[j]=dis;
		}
		i++;
	}
	printf("%.2lf",a[n-m+1]);
	return 0;
}

参考

https://www.luogu.com.cn/blog/wyz598085788/solution-p4047