zxy
ZXY标准瓦片 |
SuperMap iServer 、iEdge支持读取ZXY规范的地图瓦片,可对接 OpenStreetMap 等互联网的瓦地图服务。ZXY规范的地图瓦片规则如下:将地图全幅显示时的图片从左上角开始,往下和往右进行切割,切割的大小默认为 256*256 像素,左上角的格网行号为 0,列号为 0,往下和往右依次递增。如下图所示:
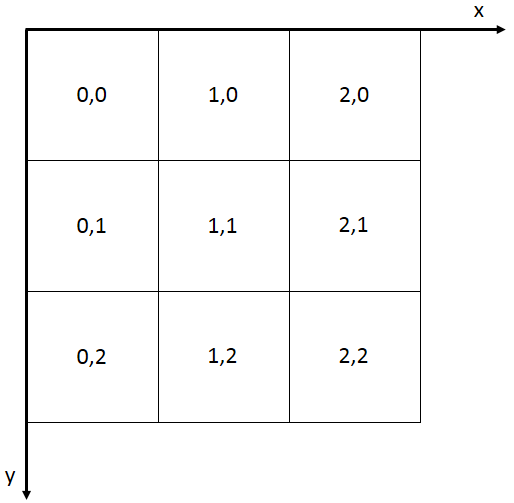
ZXY规范的地图瓦片仅支持 Web Mercator 坐标系(即 PCS_WGS_1984_WORLD_MERCATOR ,EPSG Code:3857)下的固定比例尺集合,如表1所示,这种比例尺定义的初始化显示级别0中包含了1张覆盖全球的256*256大小的切片,并且定义原点坐标为(-20037508.34,20037508.34),即全球范围的左上角。
表1 zxyTileImage 资源各显示级别参数列表
| 显示级别 | 地图宽高 (像素) | 切片数量 | 地面分辨率(米 / 像素) | 地图比例尺(96 dpi) |
| 0 | 256 | 1 | 156543.033928 | 1:591658710.909131 |
| 1 | 512 | 4 | 78271.516964 | 1:295829355.454566 |
| 2 | 1024 | 16 | 39135.758482 | 1:147914677.727283 |
| 3 | 2048 | 64 | 19567.879241 | 1:73957338.863641 |
| 4 | 4096 | 256 | 9783.939621 | 1:36978669.431821 |
| 5 | 8192 | 1024 | 4891.969810 | 1:18489334.715910 |
| 6 | 16384 | 4096 | 2445.984905 | 1:9244667.357955 |
| 7 | 32768 | 16384 | 1222.992453 | 1:4622333.678978 |
| 8 | 65536 | 65536 | 611.496226 | 1:2311166.839489 |
| 9 | 131072 | 262144 | 305.748113 | 1:1155583.419744 |
| 10 | 262144 | 1048576 | 152.874057 | 1:577791.709872 |
| 11 | 524288 | 4194304 | 76.437028 | 1:288895.854936 |
| 12 | 1048576 | 16777216 | 38.218514 | 1:144447.927468 |
| 13 | 2097152 | 67108864 | 19.109257 | 1:72223.963734 |
| 14 | 4194304 | 268435456 | 9.554629 | 1:36111.981867 |
| 15 | 8388608 | 1073741824 | 4.777314 | 1:18055.990934 |
| 16 | 16777216 | 4294967296 | 2.388657 | 1:9027.995467 |
| 17 | 33554432 | 17179869184 | 1.194329 | 1:4513.997733 |
| 18 | 67108864 | 68719476736 | 0.597164 | 1:2256.998867 |
| 19 | 134217728 | 274877906944 | 0.298582 | 1:1128.499433 |
| 20 | 268435456 | 1099511627776 | 0.149291 | 1:564.249717 |
| 21 | 536870912 | 4398046511104 | 0.074646 | 1:282.124858 |
| 22 | 1073741824 | 17592186044416 | 0.037323 | 1:141.062429 |
| 23 | 2147483648 | 70368744177664 | 0.0186615 | 1:70.5312145 |
zxy的更多相关文章
- zxy的猪错误
我觉得这篇文章还是要重构啊,如果哪道题调的久了就标上日期放上来吧. 2021/3/10 题目:玩游戏 \(\tt memset\) 不能直接清空一个指针指向的数组,因为不知道 \(\tt size\) ...
- Solution -「简单 DP」zxy 讲课记实
魔法题位面级乱杀. 「JOISC 2020 Day4」治疗计划 因为是不太聪明的 Joker,我就从头开始理思路了.中途也会说一些和 DP 算法本身有关的杂谈,给自己的冗长题解找借口. 首先,治疗方案 ...
- java web学习总结(五) -------------------servlet开发(一)
一.Servlet简介 Servlet是sun公司提供的一门用于开发动态web资源的技术. Sun公司在其API中提供了一个servlet接口,用户若想用发一个动态web资源(即开发一个Java程序向 ...
- 万向节锁(Gimbal Lock)的理解
[TOC] 结论 我直接抛出结论: Gimbal Lock 产生的原因不是欧拉角也不是旋转顺序,而是我們的思维方式和程序的执行逻辑没有对应,也就是说是我们的观念导致这个情况的发生. 他人解释 首先我们 ...
- MongoDB【第三篇】MongoDB基本操作
MongoDB的基本操作包括文档的创建.删除.和更新 文档插入 1.插入 #查看当前都有哪些数据库 > show dbs; local 0.000GB tim 0.000GB #使用 tim数据 ...
- mysql深入浅出的笔记(存储过程二)
1.条件的定义和处理可以用来定义在处理过程中遇到问题时相应的处理步揍: DECLARE condition_name CONDITION FOR condition_value condition_v ...
- 用PHP抓取页面并分析
在做抓取前,记得把php.ini中的max_execution_time设置的大点,不然会报错的.
- 会务准备期间材料准备工作具体实施总结 ----(vim技巧应用, python信息提取与整合, microsoft word格式调整批量化)
会务准备期间材料准备工作具体实施总结(vim, python, microsoft word) span.kw { color: #007020; font-weight: bold; } code ...
- Git 初始化版本库
创建带工作区的版本库 在开始一个新项目时,首先就要创建并初始化代码库.如果是在本机的工作目录中,那么: $ git init 也就够用了.如果想要初始化的版本库不在当前目录,需要为 git init ...
随机推荐
- 获取淘宝客推广位id(adzone_id)
在 获取淘宝联盟选品库的宝贝信息 这个接口中需要用到 推广位id,那边这个ID在哪找呢?1.进入阿里妈妈后台>推广管理>推广位管理,如下图: 2.在推广位管理 列表页 找到 PID,最后一 ...
- 双端队列 【deque】
题目链接:https://ac.nowcoder.com/acm/contest/1071/D 还是第一次简单运用双端队列.顾名思义:队列的头尾都可以进行插入跟删除操作. 存在于头文件 deque 中 ...
- 亿级Web系统搭建――单机到分布式集群 转载
当一个Web系统从日访问量10万逐步增长到1000万,甚至超过1亿的过程中,Web系统承受的压力会越来越大,在这个过程中,我们会遇到很多的问题.为了解决这些性能压力带来问题,我们需要在Web系统架构层 ...
- idea启动tomcat时报错:Error during artifact deployment. See server log for details.
Error during artifact deployment. See server log for details. 这个很多人都找不出来,原因无非2个: 一.jar 包有有些没能识别,tomc ...
- 【LOJ】#3102. 「JSOI2019」神经网络
LOJ#3102. 「JSOI2019」神经网络 首先我们容易发现就是把树拆成若干条链,然后要求这些链排在一个环上,同一棵树的链不相邻 把树拆成链可以用一个简单(但是需要复杂的分类讨论)的树背包实现 ...
- 2.安装阿里yum源
1.删除自带的yum源:#cd /etc/yum.repos.d/#rm -rf * 2.配置远程yum源:wget -O /etc/yum.repos.d/CentOS-Base.repo ht ...
- javascript之取余数、去商、天花板取整、地板取整
demo1: console.log('//求余数'); //求余数 console.log(5 % 4); console.log(6 % 4); //求商 console.log('//求商'); ...
- CCF - CCSP 2018-01 绝地求生 BFS
BFS从安全地区方向搞一下就好了 1.还是注意每回合清空 2.posx居然开小了,可不能犯这种错误 3.地图用a和节点的dis重名了,建议其他变量禁止用a命名 4.在输入数据之前continue了,这 ...
- Inversion 多校签到题
存下值和下标后排序,每次从坐后面开始取就可以了. ac代码: #include <algorithm> #include <cstdio> #include <cstri ...
- git 操作实践
git操作: - git是一个用于帮助用户实现版本控制的软件 #首先创建项目 1. cd到项目文件目录 2. 鼠标右键点击 Git Bash Here 3. git init #在项目文件目录生成 . ...
