java实现哈夫曼树进行文件加解压
1.哈夫曼树简述
- 给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。
- 为什么使用哈夫曼编码压缩文件?
- 一个字符八个bits,若使用编码来表示字母,节省空间,传输速度快。根据字母出现的频率构建哈夫曼树,频数即为权值,频数出现最多的字母更靠近哈夫曼树的根节点,编码长度也更短。

2.构造树的节点
- 先构造一个哈夫曼树的节点类,节点类包含5个元素:指向左节点、右节点的指针、代表的字母、频数和对应编码。
private HaffNode left,right;
private char ch;
private int n;
private String code;
- 复写节点类的compareTo方法,方便排序。
//便于使用列表排序
@Override
public int compareTo(Object o) {
HaffNode a=(HaffNode)o;
if(this.n>a.n)
return 1;
else if(this.n==a.n)
return 0;
else
return -1;
}
3.构造哈夫曼树的类(压缩)
- 构造一个哈夫曼树类,类中有6个元素:包含26个字母和空格的字符数组、读取文件得到的字符数组、保存各个节点权值的整数数组、哈夫曼树的根节点,哈夫曼树的列表形式,以及保存各个节点编码值的字符串数组。
//创立字母表
private static char[] ch={'a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z',' '};
//文件内容的字符数组
private char[] a=new char[100];
//各个字符的频数
private int[] sum=new int[27];
//树的根节点
private HaffNode root;
//保存压缩文件的单个编码
private String[] strings=new String[28];
//哈夫曼树的列表形式
private LinkedList treelist=new LinkedList<HaffNode>();
- 读取未压缩文件
//从文件中读取字节流,并保存为字符数组
public void read(String path,String name) throws IOException {
int i=0;
File f=new File(path,name);
Reader reader=new FileReader(f);
while(reader.ready()){
a[i++]=(char)reader.read();
}
reader.close();
System.out.print("压缩前的文件内容为:");
for(int k=0;k<a.length;k++){
System.out.print(a[k]);
}
System.out.println();
}
- 进行频数统计
//统计各个字母的频次
public void count(){
for(int k=0;k<a.length;k++){
for (int j=0;j<ch.length;j++){
if(a[k]==ch[j])
sum[j]++;
}
}
}
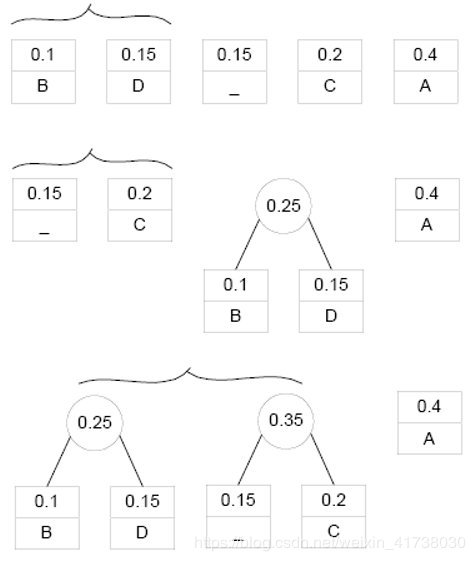
- 构造一棵哈夫曼树,将所有节点都加入列表后先排序一次。当列表长度大于1时,每次选取两个列表中权值最小的节点(也就是列表第1位和第2位的节点),构成一个字符为空的父节点,列表中删除这两个节点,把父节点加入列表后,对列表再次排序,循环到列表中只剩下一个节点时,该节点为根节点,保存。
//构造哈夫曼树,保存树的根节点
public LinkedList createTree() {
count();
//匹配频数和字符构成节点,全部加入树的列表
for (int i = 0; i < 27; i++) {
HaffNode node = new HaffNode();
node.setCh(ch[i]);
node.setN(sum[i]);
treelist.add(i, node);
}
Collections.sort(treelist);
while (treelist.size() > 1) {
//获得两个权值最小的节点
HaffNode first = (HaffNode) treelist.removeFirst();
HaffNode second = (HaffNode) treelist.removeFirst();
//将这两个权值最小的节点构造成父节点
HaffNode parent = new HaffNode();
parent.setN(first.getN() + second.getN());
parent.setLeft(first);
parent.setRight(second);
//把父节点添加进列表,并重新排序
treelist.add(parent);
Collections.sort(treelist);
}
root= (HaffNode) treelist.getFirst();
}
- 根据哈夫曼树获取编码:左子树编码为0,右子树编码为1;默认左右子树中频数较大的放右边。
//根据构建好的哈夫曼树获得各节点编码
public void getCode(HaffNode root,String code){
if(root.getLeft()!=null){
getCode(root.getLeft(),code+"0");
}
if(root.getRight()!=null){
getCode(root.getRight(),code+"1");
}
if(root.getRight()==null&&root.getLeft()==null){
System.out.println(root.getCh()+"的频次是"+root.getN()+",编码是"+code);
root.setCode(code);
return treelist;
}
}
- 根据编码转换文件内容的格式,并将转换后的结果存入文件。存入文件时写入频数表(存入字符+频数,以逗号分割,例如“a2,b3”表示a出现了2次,b出现了3次),文件内容的编码之间以空格分割,便于解压。
//文件压缩:格式转换与文件写入
public void Compress(String path) throws IOException {
String result="";
for(int i=0;i<27;i++){
result+=ch[i]+""+sum[i]+",";
}
String content="";
for(int i=0;i<a.length;i++){
for(int k=0;k<ch.length;k++){
if(a[i]==ch[k])
content+=search(root,ch[k]).getCode()+" ";
}
}
result+=content;
File f=new File(path);
if(!f.exists()){
f.createNewFile();
}
System.out.println("编码结果为:"+content);
Writer writer=new FileWriter(f);
BufferedWriter bufferedWriter=new BufferedWriter(writer);
bufferedWriter.write(result);
bufferedWriter.flush();
bufferedWriter.close();
}
- 写入一个search()方法,根据字符找到节点,从而找到该字符编码
public HaffNode search(HaffNode root,char c) {
if(root.getCh()==c){
return root;
}
if(root.getLeft()!=null||root.getRight()!=null) {
HaffNode a=search(root.getLeft(),c);
HaffNode b=search(root.getRight(),c);
if(a!=null)
return a;
if(b!=null)
return b;
}
return null;
}
4.构造哈夫曼树的类(解压)
- 解压的相关方法可以和加压的相关方法放在同一个哈夫曼树的类里,共用相同的私有变量,互不影响。为了便于区分,这里将两个过程分开来写。
- 获取压缩后的文件:
public void read2(String path,String name) throws IOException {
//读取文件
File file=new File(path,name);
Reader reader=new FileReader(file);
BufferedReader bufferedReader=new BufferedReader((new InputStreamReader(new FileInputStream(file),"GBK")));
String str="";
String temp="";
while((temp=bufferedReader.readLine())!=null){
System.out.println("解压前文件内容:"+temp);
str=temp;
}
//获取每个字符的频数(使用逗号分割),以及文件压缩后的内容
StringTokenizer s =new StringTokenizer(str,",");
int i=0;
while (s.hasMoreTokens()){
strings[i++]=s.nextToken();
}
}
- 根据频数造树:只有在添加节点时和压缩的方法有区别,分解表示频数的字符串,第一位表示字符,第二位表示频数,例如“a2”。
public LinkedList createTree2(){
for(int i=0;i<27;i++){
HaffNode temp=new HaffNode();
temp.setCh(strings[i].charAt(0));
temp.setN(strings[i].charAt(1)-'0');
treelist.add(temp);
}
Collections.sort(treelist);
while (treelist.size() > 1) {
//获得两个权值最小的节点
HaffNode first = (HaffNode) treelist.removeFirst();
HaffNode second = (HaffNode) treelist.removeFirst();
//将这两个权值最小的节点构造成父节点
HaffNode parent = new HaffNode();
parent.setN(first.getN() + second.getN());
parent.setLeft(first);
parent.setRight(second);
//把父节点添加进列表,并重新排序
treelist.add(parent);
Collections.sort(treelist);
}
root= (HaffNode) treelist.getFirst();
return treelist;
}
- 根据哈夫曼树获得编码:直接复用压缩里的getCode()方法。
- 开始解压,同样写了一个search2()方法用来根据编码寻找节点,进而找到对应字符进行格式转换。
//格式转换与文件写入
public void reCompress(String path) throws IOException {
String t=strings[27];
String result="";
StringTokenizer stringTokenizer=new StringTokenizer(t);
while(stringTokenizer.hasMoreTokens()){
String temp=stringTokenizer.nextToken();
result+=search2(root,temp).getCh();
}
System.out.println("解压后的文件内容为:"+result);
File f=new File(path);
Writer writer=new FileWriter(f);
BufferedWriter bufferedWriter=new BufferedWriter(writer);
bufferedWriter.write(result);
bufferedWriter.flush();
bufferedWriter.close();
}
public HaffNode search2(HaffNode root,String code) {
if (root.getCode() == null) {
if (root.getLeft() != null || root.getRight() != null) {
HaffNode a = search2(root.getLeft(), code);
HaffNode b = search2(root.getRight(), code);
if (a != null)
return a;
if (b != null)
return b;
}
return null;
}
else if(root.getCode().equals(code)){
return root;
}
return null;
5.整体工程文件(包括测试类)
- 节点类
public class HaffNode implements Comparable {
private HaffNode left,right;
private char ch;
private int n;
private String code;
public void setLeft(HaffNode left) {
this.left = left;
}
public void setRight(HaffNode right) {
this.right = right;
}
public void setCh(char ch) {
this.ch = ch;
}
public void setN(int sum) {
this.n = sum;
}
public void setCode(String code) {
this.code = code;
}
public HaffNode getLeft() {
return left;
}
public HaffNode getRight() {
return right;
}
public char getCh() {
return ch;
}
public int getN() {
return n;
}
public String getCode() {
return code;
}
//便于使用列表排序
@Override
public int compareTo(Object o) {
HaffNode a=(HaffNode)o;
if(this.n>a.n)
return 1;
else if(this.n==a.n)
return 0;
else
return -1;
}
@Override
public String toString() {
return getCh()+"的频次是"+getN()+",编码为"+getCode();
}
}
- 哈夫曼树类
import java.io.*;
import java.util.*;
public class HaffmanTree {
//创立字母表
private static char[] ch={'a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z',' '};
private char[] a=new char[100];
private int[] sum=new int[27];
private HaffNode root;
//保存压缩文件的单个编码
private String[] strings=new String[28];
//哈夫曼树的列表形式
private LinkedList treelist=new LinkedList<HaffNode>();
//构造哈夫曼树,保存树的根节点
public LinkedList createTree() {
count();
//匹配频数和字符构成节点,全部加入树的列表
for (int i = 0; i < 27; i++) {
HaffNode node = new HaffNode();
node.setCh(ch[i]);
node.setN(sum[i]);
treelist.add(i, node);
}
Collections.sort(treelist);
while (treelist.size() > 1) {
//获得两个权值最小的节点
HaffNode first = (HaffNode) treelist.removeFirst();
HaffNode second = (HaffNode) treelist.removeFirst();
//将这两个权值最小的节点构造成父节点
HaffNode parent = new HaffNode();
parent.setN(first.getN() + second.getN());
parent.setLeft(first);
parent.setRight(second);
//把父节点添加进列表,并重新排序
treelist.add(parent);
Collections.sort(treelist);
}
root= (HaffNode) treelist.getFirst();
return treelist;
}
//根据哈夫曼树获得各节点编码
public void getCode(HaffNode root,String code){
if(root.getLeft()!=null){
getCode(root.getLeft(),code+"0");
}
if(root.getRight()!=null){
getCode(root.getRight(),code+"1");
}
if(root.getRight()==null&&root.getLeft()==null){
System.out.println(root.getCh()+"的频次是"+root.getN()+",编码是"+code);
root.setCode(code);
}
}
public void read(String path,String name) throws IOException {
//从文件中读取字节流
int i=0;
File f=new File(path,name);
Reader reader=new FileReader(f);
while(reader.ready()){
a[i++]=(char)reader.read();
}
reader.close();
System.out.print("压缩前的文件内容为:");
for(int k=0;k<a.length;k++){
System.out.print(a[k]);
}
System.out.println();
}
public void count(){
//统计各个字母的频次
for(int k=0;k<a.length;k++){
for (int j=0;j<ch.length;j++){
if(a[k]==ch[j])
sum[j]++;
}
}
}
//文件压缩
public void Compress(String path) throws IOException {
String result="";
for(int i=0;i<27;i++){
result+=ch[i]+""+sum[i]+",";
}
String content="";
for(int i=0;i<a.length;i++){
for(int k=0;k<ch.length;k++){
if(a[i]==ch[k])
content+=search(root,ch[k]).getCode()+" ";
}
}
result+=content;
File f=new File(path);
if(!f.exists()){
f.createNewFile();
}
System.out.println("编码结果为:"+content);
Writer writer=new FileWriter(f);
BufferedWriter bufferedWriter=new BufferedWriter(writer);
bufferedWriter.write(result);
bufferedWriter.flush();
bufferedWriter.close();
}
public HaffNode search(HaffNode root,char c) {
if(root.getCh()==c){
return root;
}
if(root.getLeft()!=null||root.getRight()!=null) {
HaffNode a=search(root.getLeft(),c);
HaffNode b=search(root.getRight(),c);
if(a!=null)
return a;
if(b!=null)
return b;
}
return null;
}
public HaffNode getRoot() {
return root;
}
public void read2(String path,String name) throws IOException {
//读取文件
File file=new File(path,name);
Reader reader=new FileReader(file);
BufferedReader bufferedReader=new BufferedReader((new InputStreamReader(new FileInputStream(file),"GBK")));
String str="";
String temp="";
while((temp=bufferedReader.readLine())!=null){
System.out.println("解压前文件内容:"+temp);
str=temp;
}
//获取每个字符的频数(使用逗号分割),以及文件压缩后的内容
StringTokenizer s =new StringTokenizer(str,",");
int i=0;
while (s.hasMoreTokens()){
strings[i++]=s.nextToken();
}
}
public LinkedList createTree2(){
for(int i=0;i<27;i++){
HaffNode temp=new HaffNode();
temp.setCh(strings[i].charAt(0));
temp.setN(strings[i].charAt(1)-'0');
treelist.add(temp);
}
Collections.sort(treelist);
while (treelist.size() > 1) {
//获得两个权值最小的节点
HaffNode first = (HaffNode) treelist.removeFirst();
HaffNode second = (HaffNode) treelist.removeFirst();
//将这两个权值最小的节点构造成父节点
HaffNode parent = new HaffNode();
parent.setN(first.getN() + second.getN());
parent.setLeft(first);
parent.setRight(second);
//把父节点添加进列表,并重新排序
treelist.add(parent);
Collections.sort(treelist);
}
root= (HaffNode) treelist.getFirst();
return treelist;
}
public void reCompress(String path) throws IOException {
String t=strings[27];
String result="";
StringTokenizer stringTokenizer=new StringTokenizer(t);
while(stringTokenizer.hasMoreTokens()){
String temp=stringTokenizer.nextToken();
result+=search2(root,temp).getCh();
}
System.out.println("解压后的文件内容为:"+result);
File f=new File(path);
Writer writer=new FileWriter(f);
BufferedWriter bufferedWriter=new BufferedWriter(writer);
bufferedWriter.write(result);
bufferedWriter.flush();
bufferedWriter.close();
}
public HaffNode search2(HaffNode root,String code) {
if (root.getCode() == null) {
if (root.getLeft() != null || root.getRight() != null) {
HaffNode a = search2(root.getLeft(), code);
HaffNode b = search2(root.getRight(), code);
if (a != null)
return a;
if (b != null)
return b;
}
return null;
}
else if(root.getCode().equals(code)){
return root;
}
return null;
}
}
- 测试主函数
import java.io.IOException;
import java.util.LinkedList;
public class HaffmanTest {
public static void main(String[] args) throws IOException {
HaffmanTree h=new HaffmanTree();
h.read("C:\\Users\\XPS\\Desktop","haha.txt");
LinkedList temp=h.createTree();
for(int i=0;i<temp.size();i++){
h.getCode((HaffNode) temp.get(i),"");
}
h.Compress("E:\\hehe.txt");
HaffmanTree r=new HaffmanTree();
r.read2("C:\\Users\\XPS\\Desktop","hehe.txt");
LinkedList temp2=r.createTree2();
for(int i=0;i<temp2.size();i++)
r.getCode((HaffNode) temp2.get(i),"");
r.reCompress("C:\\Users\\XPS\\Desktop\\haha1.txt");
}
}
6.结果
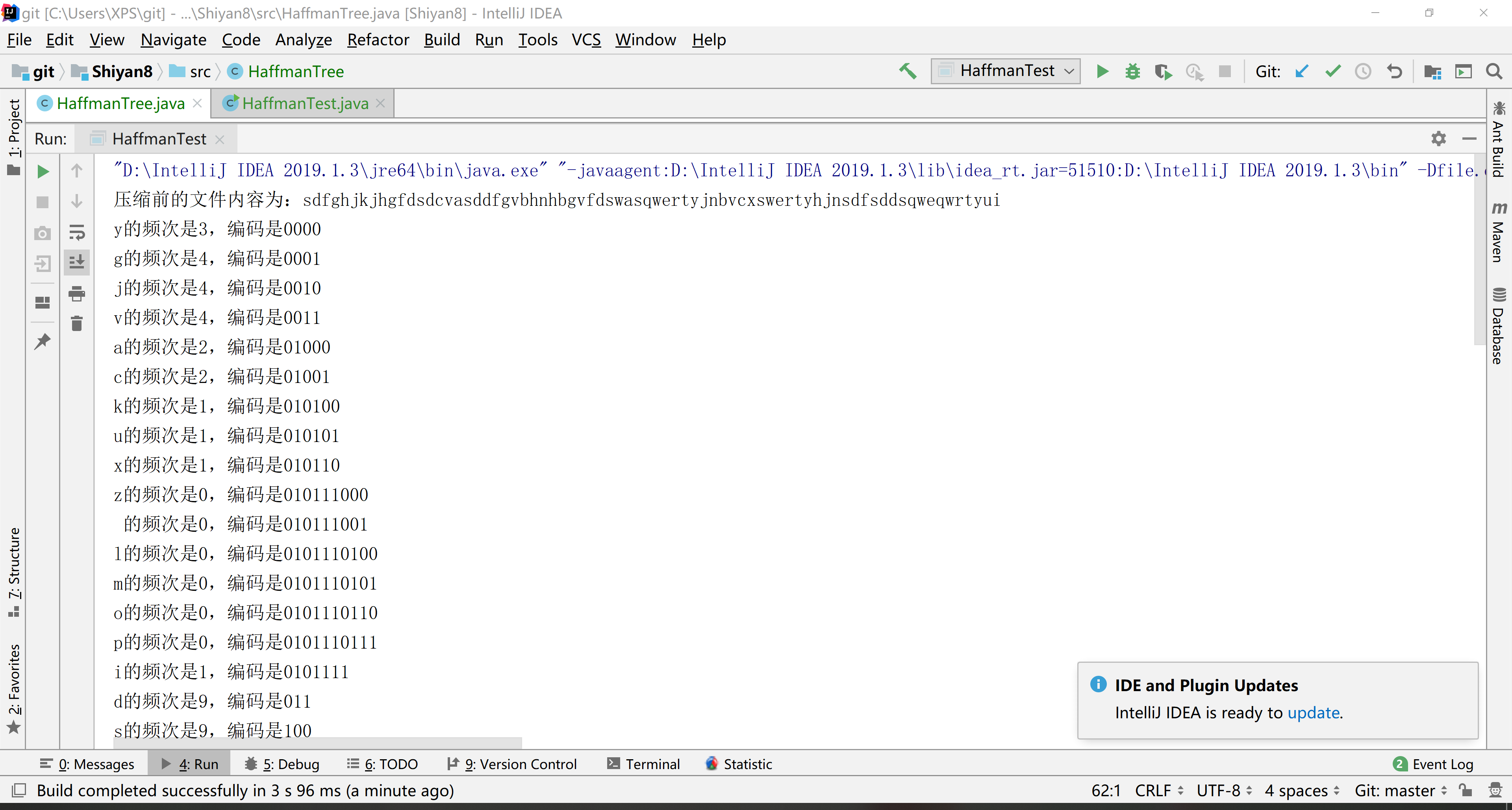
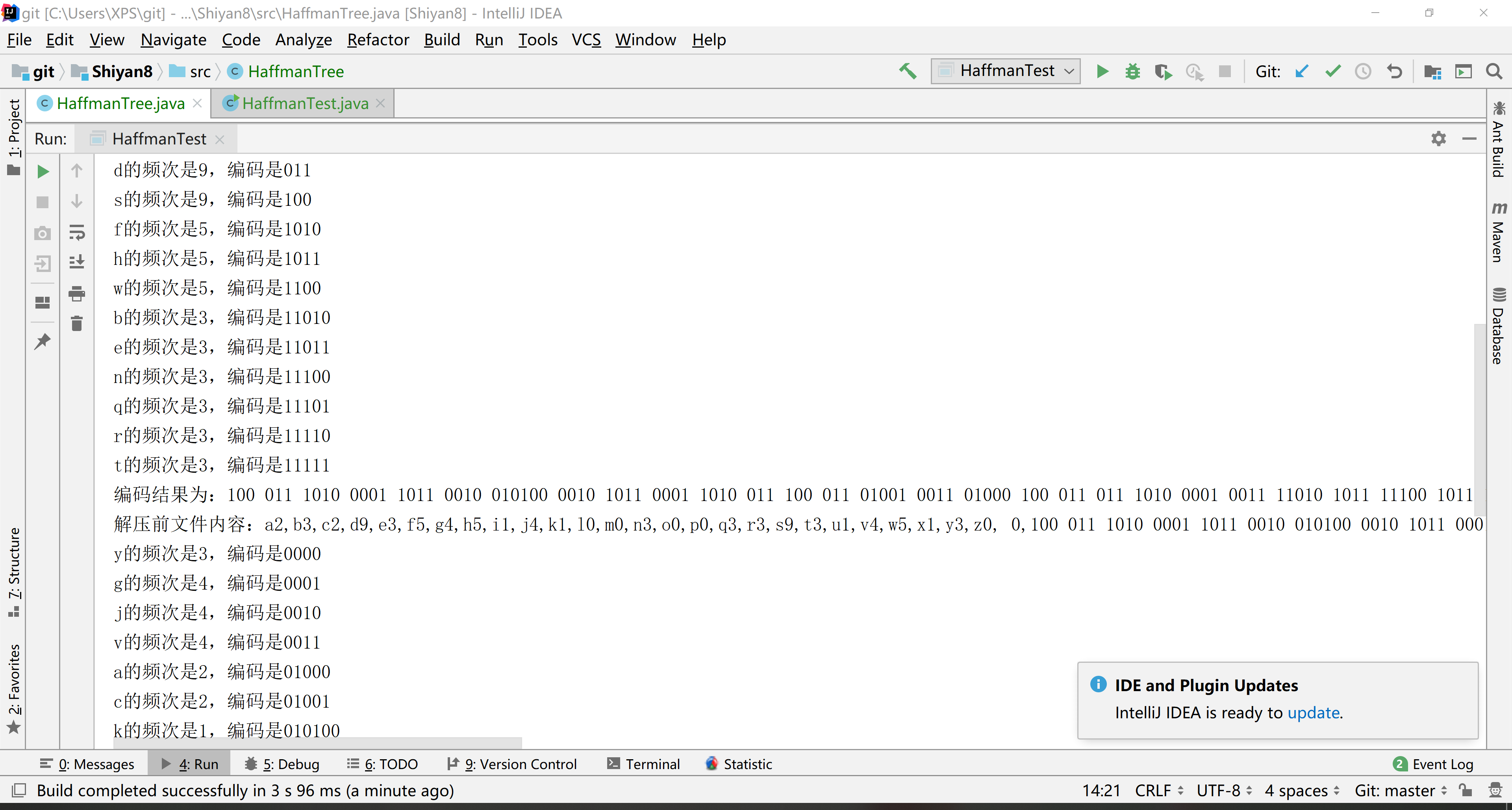
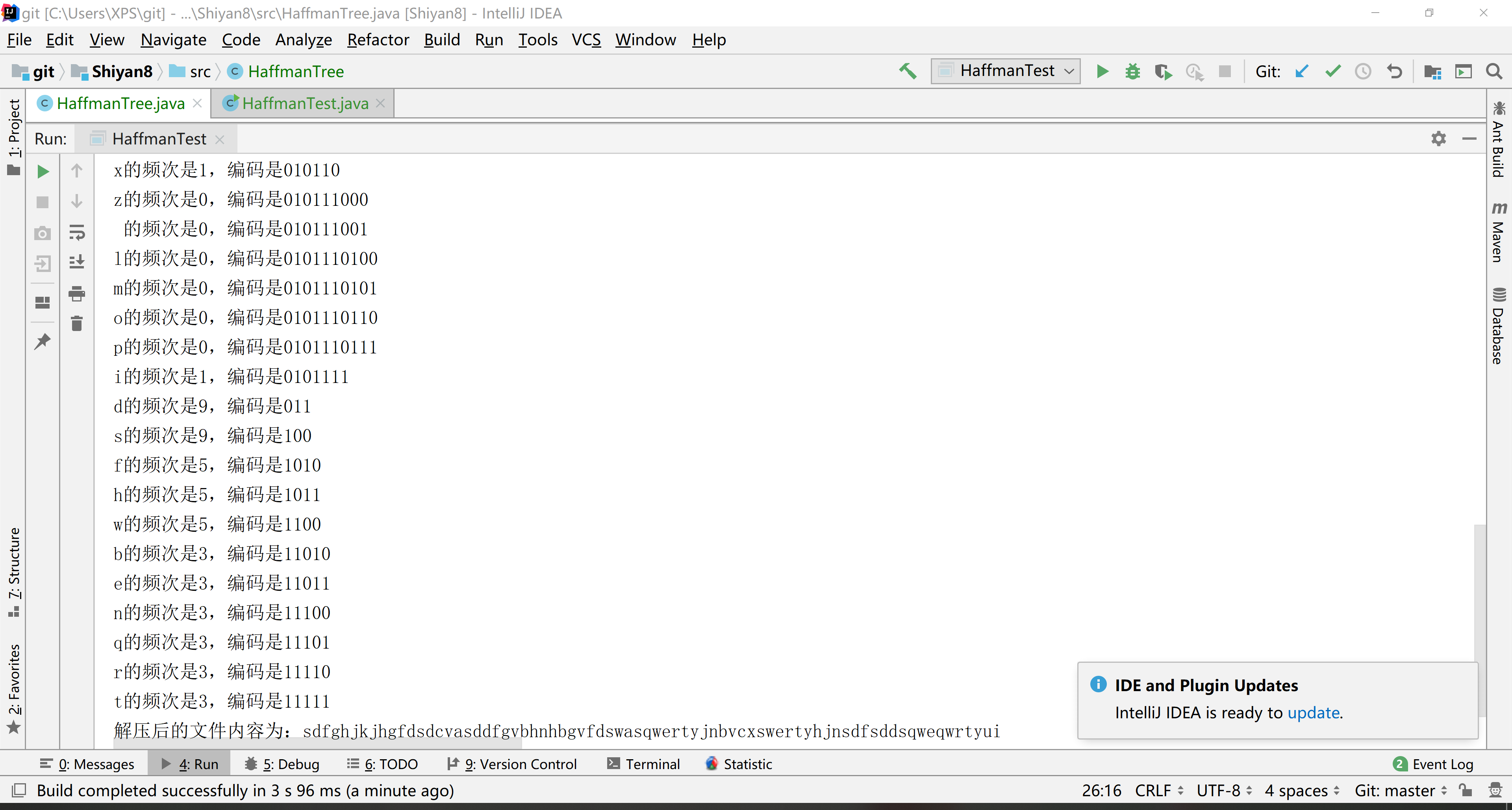
7.参考链接
java实现哈夫曼树进行文件加解压的更多相关文章
- 哈夫曼树C++实现详解
哈夫曼树的介绍 Huffman Tree,中文名是哈夫曼树或霍夫曼树,它是最优二叉树. 定义:给定n个权值作为n个叶子结点,构造一棵二叉树,若树的带权路径长度达到最小,则这棵树被称为哈夫曼树. 这个定 ...
- 哈夫曼树(三)之 Java详解
前面分别通过C和C++实现了哈夫曼树,本章给出哈夫曼树的java版本. 目录 1. 哈夫曼树的介绍 2. 哈夫曼树的图文解析 3. 哈夫曼树的基本操作 4. 哈夫曼树的完整源码 转载请注明出处:htt ...
- Java数据结构(十二)—— 霍夫曼树及霍夫曼编码
霍夫曼树 基本介绍和创建 基本介绍 又称哈夫曼树,赫夫曼树 给定n个权值作为n个叶子节点,构造一棵二叉树,若该树的带权路径长度(wpl)达到最小,称为最优二叉树 霍夫曼树是带权路径长度最短的树,权值较 ...
- Java数据结构和算法(四)赫夫曼树
Java数据结构和算法(四)赫夫曼树 数据结构与算法目录(https://www.cnblogs.com/binarylei/p/10115867.html) 赫夫曼树又称为最优二叉树,赫夫曼树的一个 ...
- 基于哈夫曼编码的文件压缩(c++版)
本博客由Rcchio原创 我了解到很多压缩文件的程序是基于哈夫曼编码来实现的,所以产生了自己用哈夫曼编码写一个压缩软件的想法,经过查阅资料和自己的思考,我用c++语言写出了该程序,并通过这篇文章来记录 ...
- 10: java数据结构和算法: 构建哈夫曼树, 获取哈夫曼编码, 使用哈夫曼编码原理对文件压缩和解压
最终结果哈夫曼树,如图所示: 直接上代码: public class HuffmanCode { public static void main(String[] args) { //获取哈夫曼树并显 ...
- 赫夫曼树JAVA实现及分析
一,介绍 1)构造赫夫曼树的算法是一个贪心算法,贪心的地方在于:总是选取当前频率(权值)最低的两个结点来进行合并,构造新结点. 2)使用最小堆来选取频率最小的节点,有助于提高算法效率,因为要选频率最低 ...
- 20172332 2017-2018-2 《程序设计与数据结构》Java哈夫曼编码实验--哈夫曼树的建立,编码与解码
20172332 2017-2018-2 <程序设计与数据结构>Java哈夫曼编码实验--哈夫曼树的建立,编码与解码 哈夫曼树 1.路径和路径长度 在一棵树中,从一个结点往下可以达到的孩子 ...
- java实现哈弗曼树和哈夫曼树压缩
本篇博文将介绍什么是哈夫曼树,并且如何在java语言中构建一棵哈夫曼树,怎么利用哈夫曼树实现对文件的压缩和解压.首先,先来了解下什么哈夫曼树. 一.哈夫曼树 哈夫曼树属于二叉树,即树的结点最多拥有2个 ...
随机推荐
- layui表单
{include file="Public:inner_header" /} <link rel="stylesheet" href="__ST ...
- Spring Cloud 之 服务网关
在微服务架构体系中,使用API 服务网关后的系统架构图如下: API服务网关的主要作用如下: 服务访问的统一入口 服务访问的负载均衡功能 服务访问的路由功能 在SpringCloud中,基于Netfl ...
- vue + jenkins 自动部署到指定的目录
1. 首先选择自由风的构建方式 2. 我的源码在gitlab上,在源码管理下,提供仓库URL和凭证,以及gitlab的分支 3. 在构建环境下选择提供Node &npm bin/folder ...
- php守护进程创建和简要分析
守护进程可 由系统启动脚本 /etc/rc.local crontab任务, 用户shell 方式运行 具体概念可参考c的 进程守护化基本步骤 1.创建子进程,终止父进程 (pcntl_fork,ex ...
- ABCD组·第五次团队作业项目需求分析改进与系统设计
项目 内容 这个作业属于哪个课程 http://www.cnblogs.com/nwnu-daizh/ 这个作业的要求在哪里 https://www.cnblogs.com/nwnu-daizh 团队 ...
- ASP.NET MVC 入门5、View与ViewData
View建立时有MVC View Page 和 MVC View Content Page两种类型, 前者为标准View, 后者为可继承Master母版页的View. Asp.Net MVC 默认使用 ...
- singleton单例模式小结
1.饿汉模式 public class SingletonEntity2 { // 在类加载的时候创建对象:饿汉模式 public static SingletonEntity2 obj = new ...
- 利用Python读取和修改Excel文件(包括xls文件和xlsx文件)——基于xlrd、xlwt和openpyxl模块
https://blog.csdn.net/sinat_28576553/article/details/81275650#4.4%C2%A0%E4%BF%9D%E5%AD%98%E5%B7%A5%E ...
- LOJ2823 三个朋友 ——查询字串的哈希值
概念 查询字串的hash值 我们所说的哈希通常都是进制哈希,因为它具有一些很方便的性质,例如,具有和前缀和类似的性质. 假设一个字符串的前缀哈希值记为 $h[i]$,进制为 $base$,那么显然 $ ...
- 微信&QQ中打开网页提示“已停止访问该网页”是怎么回事?
背景 大家是不是经常会遇到这种情况,分享出去的网页链接在微信里或者QQ里打开会提示“已停止访问该网页”,当大家看到这种的提示的时候就说明你访问的网页已经被腾讯拦截了. 当大家遇到以上这种情况的时候要怎 ...
