codeforces1187E

题目链接：http://codeforces.com/problemset/problem/1187/E

E. Tree Painting

You are given a tree (an undirected connected acyclic graph) consisting of nn vertices. You are playing a game on this tree.

Initially all vertices are white. On the first turn of the game you choose one vertex and paint it black. Then on each turn you choose a white vertex adjacent (connected by an edge) to any black vertex and paint it black.

Each time when you choose a vertex (even during the first turn), you gain the number of points equal to the size of the connected component consisting only of white vertices that contains the chosen vertex. The game ends when all vertices are painted black.

Let's see the following example:

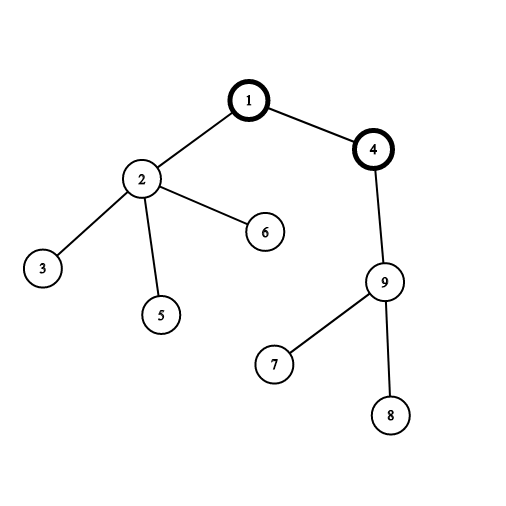
Vertices 1 and 4 are painted black already. If you choose the vertex 2, you will gain 4 points for the connected component consisting of vertices 2,3,5 and 6.

If you choose the vertex 9, you will gain 3 points for the connected component consisting of vertices 7,8 and 9.

Your task is to maximize the number of points you gain.

Input

The first line contains an integer nn — the number of vertices in the tree (2≤n≤2⋅10⁵).

Each of the next n−1 lines describes an edge of the tree. Edge i is denoted by two integers ui and vi, the indices of vertices it connects (1≤ui,vi≤n, ui≠vi).

It is guaranteed that the given edges form a tree.

Output

Print one integer — the maximum number of points you gain if you will play optimally.

Examples

input

9
1 2
2 3
2 5
2 6
1 4
4 9
9 7
9 8

output

36

input

5
1 2
1 3
2 4
2 5

output

14

Note

The first example tree is shown in the problem statement.

题意：给你一棵树，给一个操作：每次选择一个已被涂黑的节点相邻的未被涂黑的节点，并获得一个值（等于与选中节点相通（不经过黑色节点，可以互相到达）的未被涂黑节点的数量）。

初始所有节点均未被涂黑，你可以任意涂黑一个节点（并获得值），然后重复上面的操作，问可以获得的值最大是多少。

思路：因为题目给我们的是一棵树，所以当我们选定一个点为根节点进行操作时，我们可以获得的值就确定了，所以我们可以随便选一个节点为根节点，然后以它的值求出以其他节点为根节点可以获得的值，最后取最大值就可以了。

代码：

#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;
struct{
    int v,next;
}edge[];
int head[];
struct{
    ll num;//子树节点数
    ll sum;//以当前节点为根节点的子树可以获得的最大值
}p[],ans[];
int cnt;
ll mx;
void add(int u,int v){
    edge[cnt].v=v;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}
void dfs(int k,int fz){
    p[k].num=;
    p[k].sum=;
    for(int i=head[k];i!=-;i=edge[i].next){
        int v=edge[i].v;
        if(v!=fz){
            dfs(v,k);
            p[k].num+=p[v].num;//计算以当前节点为根节点的子树节点数
            p[k].sum+=p[v].sum+p[v].num;//计算值
        }
    }
}
void dfs1(int k,int fz){
    if(fz==){
        ans[k].num=p[k].num;
        ans[k].sum=p[k].sum;
    }
    else{
        ans[k].sum=p[k].sum+ans[fz].sum-p[k].num-p[k].sum+ans[fz].num-p[k].num;//我们已经知道他父亲节点的值
        //我们可以把当前节点看着父节点，父亲节点看着他的儿子节点，然后就可以和dfs中求值一样求了 

        ans[k].num=ans[fz].num;
    }
    //printf("%d %lld %lld %d %lld %lld\n",k,ans[k].num,ans[k].sum,fz,ans[fz].num,ans[fz].sum);
    mx=max(mx,ans[k].sum);
    for(int i=head[k];i!=-;i=edge[i].next){
        int v=edge[i].v;
        if(v!=fz){
            dfs1(v,k);
        }
    }
}
int main(){
    int n;
    cnt=;
    mx=;
    scanf("%d",&n);
    int u,v;
    fill(head,head+n+,-);
    for(int i=;i<n;i++){
        scanf("%d%d",&u,&v);
        add(u,v);
        add(v,u);
    }
    dfs(,);//随便以一个点为根节点求值
    dfs1(,);
    printf("%lld\n",mx);
    return ;
}