[C++]哈夫曼树(最优满二叉树) / 哈夫曼编码(贪心算法)

一 哈夫曼树

1.1 基本概念

• 算法思想
  • 贪心算法（以局部最优，谋求全局最优）
    • 适用范围
      • 1 【(约束)可行】：它必须满足问题的约束
      • 2 【局部最优】它是当前步骤中所有可行选择中最佳的局部选择
      • 3 【不可取消】选择一旦做出，在算法的后面步骤中，就无法再改变。
    • 示例
      • 【树论：最优（二叉）数=带权路径最短的树】
        • 哈夫曼（树）编码
      • 【图论：最小（代价）生成树】
        • 普里姆算法（Prim）（加点法，归并点）
        • 克鲁斯卡尔（Kruskal）算法（加边法，归并边）
      • 【图论：单源最短路径=从某一结点出发至其他结点的带权路径之和最小 / 多源最短路径=某一对结点之间的带权路径之和最小】
        • 迪杰斯特拉算法（Dijskra）
• 定义
  • 哈夫曼树 = 最优((满)二叉)树 = 带权路径之和最短的树
  • 哈夫曼树所产生的哈夫曼编码 = (最优)前缀编码
    • 一种最基本的、数据压缩的编码方法

1.2 算法描述/构造过程

1.3 算法实现

• 1> 定义存储结构

# define MAXNEGATIVE -9999 //最大负值
# define MAXPOSITIVE  9999 //最大正值 

typedef struct HuffmanNode{ // 加 typedef : 避免发生编译错误 " variable or field 'functionName' declared void "
	double weight;
	int parent, lchild, rchild; //当前节点的双亲结点、左右孩子结点
}*HuffmanTree;

• 2> 确定最小的两个结点的选择策略（贪婪策略）【次核心】

/**
 * 选择权值结点最小的两个结点 s1、s2
 */
void Select(HuffmanTree &HT,int k,int *s1,int *s2){
	int min[2]={0, 0}; // 升序排名， 保留 HT中 权重值最小的两个结点的下标
	cout<<"Select k:"<<k<<endl;
	HT[0].weight = MAXPOSITIVE; // 初始化为最大正值，方便被 初始结点比最小而比下去
	for(int i=1;i<=k;i++){
//		cout<<"i:"<<i<<"\tweight:"<<HT[i].weight<<"\tparent:"<<HT[i].parent<<"\tparent.weight:"<<HT[HT[i].parent].weight<<endl;
		if( HT[i].parent==0 && (HT[i].weight<HT[min[1]].weight)){
			if(HT[i].weight<HT[min[0]].weight){ // 小于 最小者
				min[1] = min[0]; min[0] = i; cout<<i<<"小于最小者！"<<endl;
			} else {
				min[1] = i;cout<<i<<"小于次小者！"<<endl;	 //仅小于 次小者
			}
		}
	}
	*s1 = min[0]; // 最小者下标
	*s2 = min[1]; // 次小者下标
//	cout<<"s1:"<<*s1<<"\ts2:"<<*s2<<endl;
}

• 3> 创建 Huffman 树【核心】

/**
 * 创建 Huffman 树
 *   n : 初试结点（待编码结点）数
 */
void CreateHuffmanTree(HuffmanTree &HT, int n){
	int m = 2*n-1;
	HT = new HuffmanNode[m+1]; // 0 位空余
	cout<<"Please input initiative node's weight : "<<endl; // 输入结点数据
	for(int i=1;i<=n;i++){
		cin>>HT[i].weight;
	}
	for(int k=1;k<=m;k++){ // 初始化所有结点
		HT[k].lchild = 0;
		HT[k].rchild = 0;
		HT[k].parent = 0;
	}
	for(int j=n+1;j<=m;j++){
		int s1,s2;
		Select(HT, j-1, &s1, &s2); // 选择权值结点最小的两个结点s1、s2
		HT[s1].parent = j; // 合并左右结点
		HT[s2].parent = j;
		HT[j].lchild = s1;
		HT[j].rchild = s2;
		HT[j].weight = HT[s1].weight + HT[s2].weight;
	}
}

• 4> 输出哈夫曼树

void OutputHuffmanTree(HuffmanTree &HT, int n){ // 输出 哈夫曼树 中 结点情况
	int m = 2*n-1;
	for(int i=1;i<=m;i++){
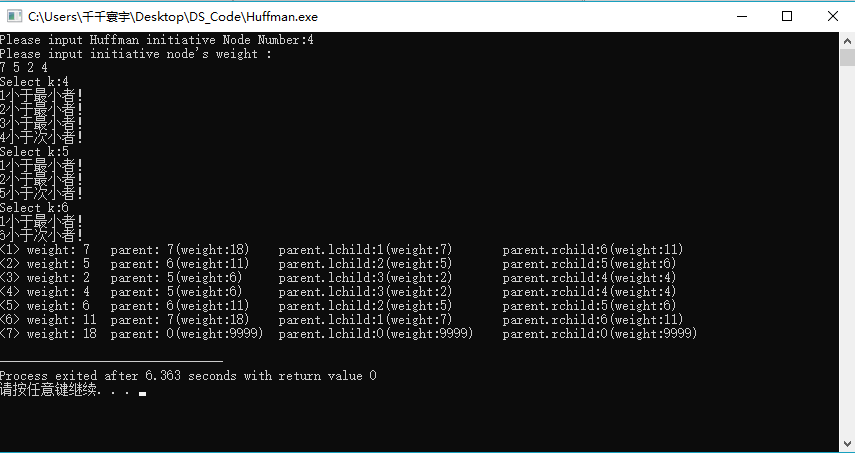
		cout<<"<"<<i<<"> weight: "<<HT[i].weight<<"\t"<<"parent: "<<HT[i].parent<<"(weight:"<<HT[HT[i].parent].weight<<")\t";
		cout<<"parent.lchild:"<<HT[HT[i].parent].lchild<<"(weight:"<<HT[HT[HT[i].parent].lchild].weight<<")"<<"\t";
		cout<<"parent.rchild:"<<HT[HT[i].parent].rchild<<"(weight:"<<HT[HT[HT[i].parent].rchild].weight<<")"<<endl;
	}
}

• 5> 执行：Main函数

int main(){
	HuffmanTree HT;
	int n;
	cout<<"Please input Huffman initiative Node Number:"; // 输入哈夫曼结点初始结点数目 n
	int s1, s2;
	cin>>n;
	CreateHuffmanTree(HT, n);
	OutputHuffmanTree(HT, n);
	return 0;
}

二 哈夫曼编码

2.1 哈夫曼编码的主要思想

2.2 【前缀编码】

2.3 【哈夫曼编码】

2.4 应用：文件的编码与译码

2.5 哈夫曼编码的算法实现 （根据哈夫曼树，求哈夫曼编码）

• 1> 定义存储结构

//由于 每个哈夫曼编码是变长编码；因此，使用指针数组来存储每个字符编码串的首地址
typedef char **HuffmanCode; // 动态分配数组，存储哈夫曼编码表 (char 前面不能随意加 struct 关键字)

• 2> 生成哈夫曼编码(表)（借助于哈夫曼树）

/**
 * 根据哈夫曼树，求哈夫曼编码
 */
void CreateHuffmanCodeByHuffmanTree(HuffmanTree HT, HuffmanCode &HC,int n){//从叶子到根，逆向求每个字符的哈夫曼编码
	HC = new char *[n+1]; // 分配存储n个字符编码的编码表空间
	char *cd = new char [n]; // 分配临时存放每个字符编码的动态数组空间
	cd[n-1] = '\0'; // 编码结束符
	for(int i=1;i<=n;i++){ // 逐个字符求哈夫曼编码
		int start = n-1; // start 初始化指向最后位置 即 编码结束符位置，逆向存储 从叶子到根结点路径的0/1编码
		int c = i;
		int f = HT[i].parent; // f 指向结点C 的双亲结点
		while(f!=0){ // 直到 f 滑动到根节点为止
			--start; // 编码表游标向前滑动
			if(HT[f].lchild == c){
				cd[start] = '0';
			} else {
				cd[start]= '1';
			}
			c = f;
			f = HT[f].parent; // 逆向， 自(树)底向(树)上
		}
		HC[i] = new char [n-start]; //为第i个字符编码分配存储空间
		strcpy(HC[i], &cd[start]); // 头文件： #include <string.h> 、<stdio.h>
	}
	delete cd;
}

• 3> 输出哈夫曼编码(表)

void OutputHuffmanCodes(HuffmanCode &HC,int n){
	for(int i=1;i<=n;i++){
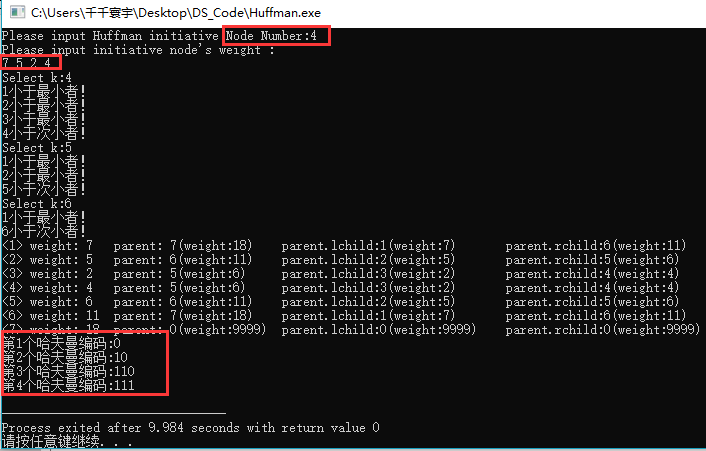
		cout<<"第"<<i<<"个哈夫曼编码:";
		for(int j=0,size=sizeof(HC[i])/sizeof(char);j<size;j++){
			cout<<HC[i][j];
		}
		cout<<endl;
	}
}

• 4> 执行：Main函数

int main(){
	HuffmanTree HT;
	int n;
	cout<<"Please input Huffman initiative Node Number:"; // 输入哈夫曼结点初始结点数目 n
	int s1, s2;
	cin>>n;
	CreateHuffmanTree(HT, n);
	OutputHuffmanTree(HT, n);

	HuffmanCode HC;
	CreateHuffmanCodeByHuffmanTree(HT, HC, n);
	OutputHuffmanCodes(HC, n);
	return 0;
}

三 哈夫曼译(解)码

四 文献

4.1 参考文献

• 《数据结构(C语言版)：严蔚敏/吴伟民》
• 《算法设计与分析基础（[美] Anany Levitin. 潘彦 译）》
  • 贪心算法思想的适用范围

4.2 推荐文献

• 《算法导论》实验四：哈夫曼（Huffman）编码问题（C++实现）

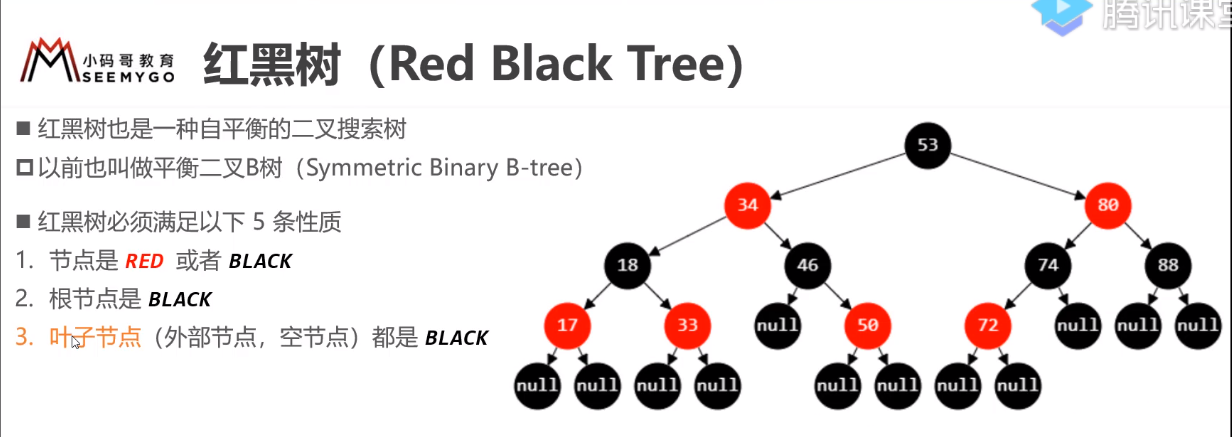
五 二叉树 补充：红黑树