洛谷 P4298: bzoj 1143: [CTSC2008]祭祀

题目传送门：洛谷 P4298。

题意简述：

给定一个 \(n\) 个点，\(m\) 条边的简单有向无环图（DAG），求出它的最长反链，并构造方案。

最长反链：一张有向无环图的最长反链为一个集合 \(S \subseteq V\)，满足对于 \(S\) 中的任意两个不同的点 \(u, v \in S\)（\(u \ne v\)），\(u\) 不能到达 \(v\)，\(v\) 也不能到达 \(u\)，且 \(S\) 的大小尽量大。

题解：

根据 Dilworth 定理，一个 DAG 中最长反链的大小，等于其中最小可重链覆盖大小。

最小可重链覆盖：在 DAG 中选出若干条链，经过每个点至少一次，一个点可被一条链经过多次，且链数尽量少。

其实 Dilworth 定理描述的是：一个偏序集中的最长反链大小，等于其中最小不可重链覆盖大小。

但是因为求出 DAG 的传递闭包后，DAG 也可以表示成偏序集的形式，所以相当于可重链覆盖。

总之先求出 DAG 的传递闭包，然后求形成的偏序集上的最小不可重链覆盖。

那么，最小不可重链覆盖应该怎么求呢？

考虑从每个点自成一条链的形态出发，此时恰好有 \(n\) 条链。

可以发现最终答案一定是合并（首尾相接）若干条链形成的。考虑重新描述这个过程：

对于一个点，它在最终的链上，一定只有最多一个前驱，和最多一个后继。

我们考虑把每个点拆成入点和出点，那么入点和出点应该只能匹配上最多一个点（表示前驱或者后继）。

这似乎是二分图匹配的形式，具体地，我们考虑：

把一个点 \(x\) 拆成两个点：\(x_{out}\) 和 \(x_{in}\)，表示出点和入点。

对于一条边 \(x \to y\)，连接 \(x_{out}\) 与 \(y_{in}\)，表示原图中 \(x\) 的出边指向 \(y\)（这条边是 \(y\) 的入边）。

那么最终形成了一个二分图，左侧是所有 \(x_{out}\)，右侧是所有 \(x_{in}\)。而且所有边都是连接左侧的点和右侧的点的。

在这个二分图 \(G = \langle \langle V_{out}, V_{in} \rangle , E' \rangle\) 上做二分图最大匹配：

每一个匹配边 \(x_{out} \leftrightarrow y_{in}\) 都可以还原原图中链的一条边 \(x \to y\)。

每匹配 \(1\) 条边，链的个数就减少 \(1\)，则有最小链覆盖的大小等于 \(n\) 减去最大匹配的大小。

继续考虑如何从二分图最大匹配中，构造出最长反链。以下部分参考了 r_64 的题解。

我们首先需要构造二分图最大独立集，这部分参考了「图的最大匹配算法」这篇博客：

考虑下图，可以求出它的其中一种最大匹配为 \(\{ \langle 2, D \rangle, \langle 3, E \rangle, \langle 4, A \rangle, \langle 5, C \rangle \}\)，设最大匹配大小为 \(m\)，这里 \(m = 4\)：

从右侧的非匹配点（这里为 \(B\)，可能有多个）开始 DFS，右侧的点只能走非匹配边向左访问，左侧的点只能走匹配边向右访问：

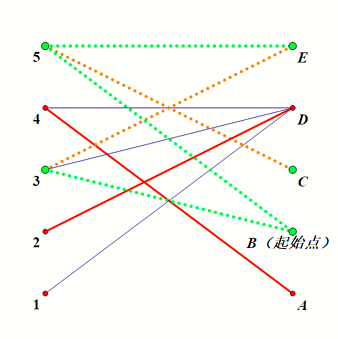
可以发现 DFS 到了 \(3, 5, B, C, E\) 这些点。

我们取左侧被 DFS 到的点，以及右侧没被 DFS 到的点，也就是 \(3, 5, A, D\) 这些点，记做集合 \(S\)，可以证明 \(S\) 是一个最小点覆盖。

最小点覆盖：选取最少的点，覆盖每条边，也就是说每条边的两个端点至少有一个被选中了。

证明：

1. 首先有：最小点覆盖等于最大匹配。我们可以证明 \(|S| = m\)。
   
   这是因为：右侧的非匹配点一定都被 DFS 到了，所以在右侧选取的必然是匹配点。如果一个右侧的匹配点没被选取，即它被 DFS 到了，而这只有可能是因为它在左侧匹配到的点被 DFS 到了，那么左侧匹配到的点就会被选上。即是：每条匹配边的两端点恰好会被选一个。而左侧的非匹配点一定不会被 DFS 到，这是因为如果被 DFS 到了，必然会形成一条交错路（匈牙利算法中的），不满足最大匹配的条件。所以有且仅有匹配边的端点会被选上，而且每条匹配边的两端点恰好被选一个，所以 \(\boldsymbol{|S| = m}\)。

2. \(S\) 可以覆盖所有的边。
   
   我们把边按照左右端点是否被 DFS 到，分成 \(2 \times 2 = 4\) 类。那么如果出现了左端点没被 DFS 到，但是右端点被 DFS 到了的边，它才不会被覆盖。然而这是不可能的，这是因为对于一个右侧被 DFS 到的点，与它相连的左侧的点一定都被 DFS 到了。

然后有最大独立集等于最小点覆盖的补集。也就是只要选出左侧没被 DFS 到的点和右侧被 DFS 到的点就行了。

在上图中就是 \(1, 2, 4, B, C, E\) 这 \(6\) 个点。

回到 DAG 的情况（注意到我们举的例子并不是 DAG 导出的二分图，所以这个例子不能用来解释最长反链）：

令最大独立集为 \(I\)，考虑选出所有 \(x_{out}\) 和 \(x_{in}\) 都属于 \(I\) 的点，记做集合 \(A\)，它们构成一个最长反链。

证明：

先证 \(A\) 的确是一个反链：这是容易的，因为任取 \(x \in A\)，\(x_{in}\) 就一定是被 DFS 到的点，而 \(x_{out}\) 一定是没被 DFS 到的点，任何两个 \(x, y \in A\) 之间若是有连边就和 DFS 的过程冲突了。

首先有 \(|I| = 2n - |S| = 2n - m\)，而 \(|I| - |A|\) 可以看作是满足「\(x_{out}\) 或 \(x_{in}\) 属于 \(I\)」的 \(x\) 的个数，显然这样的 \(x\) 不会超过 \(n\) 个，所以 \(|I| - |A| \le n\)，所以 \(|A| \ge |I| - n = n - m\)。

但是 \(A\) 再大，也不能大过 \(n - m\)，所以 \(|A| = n - m\)，也就是一个最长反链。

总结：只要选出 \(x_{out}\) 没被 DFS 到，且 \(x_{in}\) 被 DFS 到了的点，这些点就组成一个最长反链。

然后是第三问，这只要默认该点被选中，也就是删除这个点和与其有偏序关系的所有点后，再求一次最长反链，如果最长反链的大小只减小了 \(1\)，那么这个点就能在最长反链中，否则不能。

下面是代码，复杂度为 \(\mathcal O (n^{3.5})\)：

#include <cstdio>
#include <algorithm>
#include <bitset>

namespace Dinic {
	const int Inf = 0x3f3f3f3f;
	const int MN = 205, MM = 5155;

	int N, S, T;
	int h[MN], iter[MN], nxt[MM * 2], to[MM * 2], w[MM * 2], tot;

	inline void Init(int _N) {
		N = _N, tot = 1;
		for (int i = 1; i <= N; ++i) h[i] = 0;
	}
	inline void SetST(int _S, int _T) { S = _S, T = _T; }

	inline void ins(int u, int v, int x) { nxt[++tot] = h[u], to[tot] = v, w[tot] = x, h[u] = tot; }
	inline void insw(int u, int v, int w1 = Inf, int w2 = 0) {
		if (!u) u = S; if (!v) v = T;
		ins(u, v, w1), ins(v, u, w2);
	}

	int lv[MN], que[MN], l, r;

	inline bool Lvl() {
		for (int i = 1; i <= N; ++i) lv[i] = 0;
		lv[S] = 1;
		que[l = r = 1] = S;
		while (l <= r) {
			int u = que[l++];
			for (int i = h[u]; i; i = nxt[i])
				if (w[i] && !lv[to[i]]) {
					lv[to[i]] = lv[u] + 1;
					que[++r] = to[i];
				}
		}
		return lv[T] != 0;
	}

	int Flow(int u, int f) {
		if (u == T) return f;
		int d = 0, s = 0;
		for (int &i = iter[u]; i; i = nxt[i])
			if (w[i] && lv[to[i]] == lv[u] + 1) {
				d = Flow(to[i], std::min(f, w[i]));
				f -= d, s += d;
				w[i] -= d, w[i ^ 1] += d;
				if (!f) break;
			}
		return s;
	}

	inline int DoDinic() {
		int Ans = 0;
		while (Lvl()) {
			for (int i = 1; i <= N; ++i) iter[i] = h[i];
			Ans += Flow(S, Inf);
		}
		return Ans;
	}
}
using Dinic::Init;
using Dinic::SetST;
using Dinic::insw;
using Dinic::DoDinic;
using Dinic::h;
using Dinic::nxt;
using Dinic::to;
using Dinic::w;

const int MN = 105;

int N, M, Ans;
std::bitset<101> g[MN];

int match[MN], tagl[MN], tagr[MN];
void DFS(int u) {
	tagr[u] = 1;
	for (int i = 1; i <= N; ++i)
		if (g[i][u] && !tagl[i])
			tagl[i] = 1, DFS(match[i]);
}

int main() {
	scanf("%d%d", &N, &M);
	for (int i = 1; i <= M; ++i) {
		int x, y;
		scanf("%d%d", &x, &y);
		g[x][y] = 1;
	}
	for (int k = 1; k <= N; ++k)
		for (int i = 1; i <= N; ++i)
			if (g[i][k]) g[i] |= g[k];
	Init(N + N + 2), SetST(N + N + 1, N + N + 2);
	for (int i = 1; i <= N; ++i)
		insw(0, i, 1), insw(N + i, 0, 1);
	for (int i = 1; i <= N; ++i)
		for (int j = 1; j <= N; ++j)
			if (g[i][j]) insw(i, N + j, 1);
	Ans = N - DoDinic();
	printf("%d\n", Ans);
	for (int i = 1; i <= N; ++i) if (!w[4 * i - 2]) {
		for (int j = h[i]; j; j = nxt[j])
			if (!w[j]) { match[i] = to[j] - N; break; }
	}
	for (int i = 1; i <= N; ++i) if (w[4 * i]) DFS(i);
	for (int i = 1; i <= N; ++i) printf("%d", !tagl[i] && tagr[i]);
	puts("");
	for (int u = 1; u <= N; ++u) {
		static int del[MN]; int cnt = 0;
		for (int i = 1; i <= N; ++i) del[i] = i == u || g[i][u] || g[u][i];
		Init(N + N + 2), SetST(N + N + 1, N + N + 2);
		for (int i = 1; i <= N; ++i) if (!del[i])
			insw(0, i, 1), insw(N + i, 0, 1), ++cnt;
		for (int i = 1; i <= N; ++i) if (!del[i])
			for (int j = 1; j <= N; ++j) if (!del[j])
				if (g[i][j]) insw(i, N + j, 1);
		printf("%d", cnt - DoDinic() == Ans - 1);
	} puts("");
	return 0;
}