@codeforces - 1086F@ Forest Fires

目录

• @description@
• @solution@
• @accepted code@
• @details@

---

@description@

一个无穷大的方格图，每个方格内都种了棵树。

一开始点燃了 n 棵树。之后的每一秒内，火都会从一个格子蔓延到共边或者共顶点的方格。t 秒后，火停止蔓延。

记 val(x, y) 为方格 (x, y) 被点燃的时间，如果未被点燃，则 val(x, y) = 0。

求所有格子的 val 之和。模 998244353。

Input

第一行两个整数 n 和 t (1≤n≤50, 0≤t≤10^8)。

接下来 n 行每行两个整数 x 与 y (−10^8≤x, y≤10^8)，表示初始着火的坐标。

保证所有坐标互不相同。

Output

输出一个整数表示 val 之和模 998244353。

Examples

Input

1 2

10 11

Output

40

Input

4 1

2 2

1 3

0 2

2 4

Output

18

Input

3 0

0 0

-2 1

1 1

Output

0

Note

以下是三个样例分别对应的图：

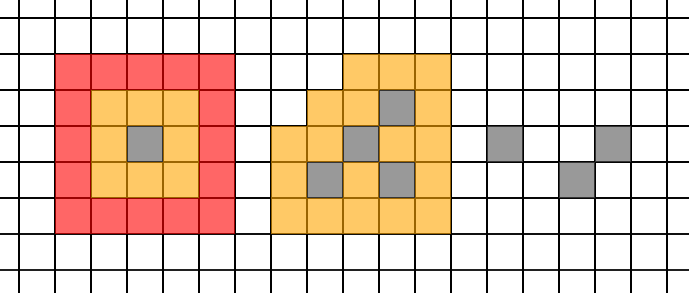
@solution@

我们先稍微转换一下问题。记 f(i) 表示 i 秒后已经着火的面积，则最终答案为：

\[ans = (t + 1)*f(t) - \sum_{i=0}^{t}f(i)
\]

当然这个转换并不是必需的，只是更方便一些。

若给定 i，求 f(i) 可以一波扫描线搞定。暴力扫描线 O(n^2)，线段树优化可以做到 O(nlogn)（但没必要啊喂）。

假如只有一个起火点，则 f(t) 呈二次函数增长。这个显然。

假如有两个起火点，当两个区域不相交时显然 f(t) 呈二次函数增长；相交时，总面积 = 面积之和 - 相交面积。

矩形的交仍是矩形，故相当于是二次函数 - 二次函数，还是个二次的函数。

假如有 n 个起火点，则根据容斥原理并仿照上面的证明，也可以得证在相交情况不变的前提下，f(t) 呈二次函数增长。

因为 a 与 b 相交，b 与 c 相交，c 与 a 相交时，可以得到 a, b 与 c 存在共同的相交部分（因为它们都是矩形）。

也就是说，矩阵两两相交的 O(n^2) 个时刻，将 f(t) 划分成 O(n^2) 个分段函数，每个函数都是个二次函数。

既然 f(t) 是二次函数，那么 \(\sum f(t)\) 自然就是一个三次函数。插值插一下就插出来啦。

@accepted code@

#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN = 50;
const int MOD = 998244353;
int pow_mod(int b, int p) {
	int ret = 1;
	while( p ) {
		if( p & 1 ) ret = 1LL*ret*b%MOD;
		b = 1LL*b*b%MOD;
		p >>= 1;
	}
	return ret;
}
inline int add(int a, int b) {return (a + b)%MOD;}
inline int mul(int a, int b) {return 1LL*a*b%MOD;}
inline int sub(int a, int b) {return add(a, (MOD - b)%MOD);}
inline int inv(int x) {return pow_mod(x, MOD - 2);}
vector<int>v1[2*MAXN + 5], v2[2*MAXN + 5];
int x[MAXN + 5], y[MAXN + 5], n;
int dx[2*MAXN + 5], dy[2*MAXN + 5], xcnt, ycnt;
int tag[2*MAXN + 5];
int func(int t) {
	xcnt = ycnt = 0;
	for(int i=1;i<=n;i++) {
		dx[++xcnt] = x[i] + t + 1, dx[++xcnt] = x[i] - t;
		dy[++ycnt] = y[i] + t + 1, dy[++ycnt] = y[i] - t;
	}
	sort(dx + 1, dx + xcnt + 1), xcnt = unique(dx + 1, dx + xcnt + 1) - dx - 1;
	sort(dy + 1, dy + ycnt + 1), ycnt = unique(dy + 1, dy + ycnt + 1) - dy - 1;
	for(int i=1;i<=xcnt;i++) v1[i].clear(), v2[i].clear();
	for(int i=1;i<=n;i++) {
		int l = lower_bound(dx + 1, dx + xcnt + 1, x[i] - t) - dx;
		int r = lower_bound(dx + 1, dx + xcnt + 1, x[i] + t + 1) - dx;
		v1[l].push_back(i), v2[r].push_back(i);
	}
	int ans = 0;
	for(int i=1;i<=xcnt;i++) {
		int tmp = 0;
		for(int j=1;j<=ycnt;j++) {
			if( tmp ) ans = add(ans, mul(dy[j] - dy[j-1], dx[i] - dx[i-1]));
			tmp += tag[j];
		}
		for(int j=0;j<v1[i].size();j++) {
			int p = v1[i][j];
			int u = lower_bound(dy + 1, dy + ycnt + 1, y[p] - t) - dy;
			int d = lower_bound(dy + 1, dy + ycnt + 1, y[p] + t + 1) - dy;
			tag[u]++, tag[d]--;
		}
		for(int j=0;j<v2[i].size();j++) {
			int p = v2[i][j];
			int u = lower_bound(dy + 1, dy + ycnt + 1, y[p] - t) - dy;
			int d = lower_bound(dy + 1, dy + ycnt + 1, y[p] + t + 1) - dy;
			tag[u]--, tag[d]++;
		}
	}
	return ans;
}
struct point{
	int x, y;
	point(int _x=0, int _y=0):x(_x), y(_y) {}
};
int func3(point *p, int x) {
	int ret = 0;
	for(int i=0;i<4;i++) {
		int del = 1;
		for(int j=0;j<4;j++)
			if( i != j ) del = mul(del, mul(sub(x, p[j].x), inv(sub(p[i].x, p[j].x))));
		ret = add(ret, mul(del, p[i].y));
	}
	return ret;
}
int func2(int l, int r) {
	if( r - l + 1 <= 3 ) {
		int ret = 0;
		for(int i=l;i<=r;i++) ret = add(ret, func(i));
		return ret;
	}
	point p[4] = {point(l, func(l))};
	for(int i=1;i<4;i++)
		p[i] = point(l + i, add(p[i - 1].y, func(l + i)));
	return (sub(func3(p, r), func3(p, l - 1)) + MOD)%MOD;
}
int a[MAXN*MAXN + 5], cnt;
int main() {
	int t; scanf("%d%d", &n, &t);
	for(int i=1;i<=n;i++)
		scanf("%d%d", &x[i], &y[i]);
	for(int i=1;i<=n;i++)
		for(int j=i+1;j<=n;j++) {
			int p = max((abs(x[i] - x[j]) - 1) >> 1, (abs(y[i] - y[j]) - 1) >> 1);
			if( p <= t ) a[++cnt] = p;
		}
	a[++cnt] = t;
	sort(a + 1, a + cnt + 1), cnt = unique(a + 1, a + cnt + 1) - a - 1;
	int ans = mul(t + 1, func(t)), lst = 0;
	for(int i=1;i<=cnt;i++)
		ans = sub(ans, func2(lst, a[i])), lst = a[i] + 1;
	printf("%d\n", ans);
}

@details@

插值点不够就直接暴力算。

一开始看错题。。。还以为是只能共边的格子传递。。。