【OI】二分图最大匹配

所谓二分图，是可以分为两个点集的图；

所谓二分图最大匹配，是两个点集之间，每两个不同点集的点连接,每个点只能连一个点，最大的连接数就是最大匹配。

如何解最大匹配，需要用到匈牙利算法。

另：本文写了很多细节，有的地方比较啰嗦，请大佬放过

---

匈牙利算法是一个递归的过程，它的特点，我觉得可以归为一个字：“让”。

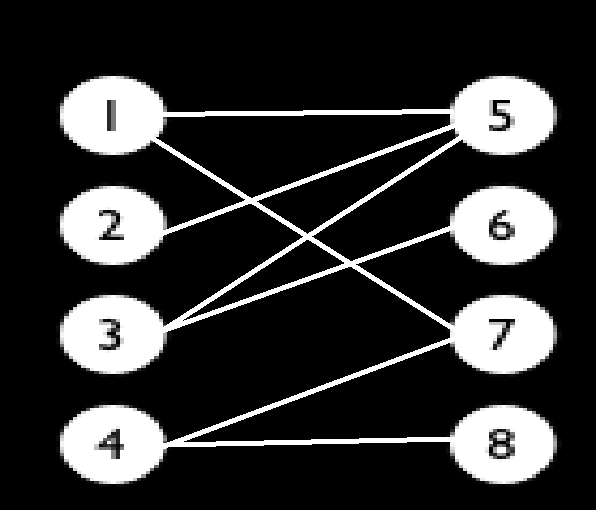
例如这张图，按照匈牙利算法的思路就是：

1.1与5匹配，5没有被标记，将5标记，记录1与5匹配

2.清空标记

3.2与5匹配，5没有被标记，将5标记，发现5已经与1匹配，在[此处]重新递归1：

　　①1与5匹配，发现5已经被标记，跳出

　　②1与7匹配，发现7没有被标记，将7标记，记录1与7匹配，返回成功

4.回到2与5匹配的[此处]，发现返回成功，则直接记录2与5匹配

5.清空标记

6.3与5匹配，5没有被标记，将5标记，发现5已经与2匹配，在[此处]重新递归2：

　　①2与5匹配，发现5已经被标记，跳出

　　②2没有其他连接的边了，返回失败

7.回到3与5匹配的[此处]，发现返回失败，继续查找与3连接的边

8.3与6匹配，6没有被标记，将6标记，记录3与6匹配

9.清空标记

9.4与7匹配，7没有被标记，将7标记，发现7已经与1匹配，在[此处]重新递归1：

　　①1与5匹配，5没有被标记，将5标记，发现5已经与2匹配，在[此处A]重新递归2：

　　　　①2与5匹配，发现5已经被标记，跳出

　　　　②2没有连接的边了，返回失败

　　②回到1与5匹配的[此处A]，发现返回失败，继续查找1连接的边

　　③1与7匹配，发现7已经被标记，跳出

　　④1没有可以连接的边了，返回失败

10.回到4与7匹配的[此处]，发现返回失败，继续查找与4连接的边

11.4与8匹配，8没有被标记，将8标记，记录4与8匹配

12.清空标记

13.左边的点集枚举完毕，从记录中得到：1与7匹配，2与5匹配，3与6匹配，4与8匹配

这就是匈牙利算法（这就是人脑编译器吗）

用人话来说，就是

1：诶，你看我找到我连接的第一个，是一个没人占据的点啊，我和5匹配吧

2：诶，你看我找到我连接的第一个就是5，竟然被1占据了！可恶，1你再去找找有没有别的边去匹配！

1：我要匹配5！

2：这是我要匹配的！

1：好吧，我看看，我连接的第二个，是一个没人占据的边啊，我和7匹配吧

2：好棒啊，那我就和5匹配了

3：我连接的第一个边是5，居然被2占据了，2你去看看有没有别的边匹配啊

2：好，我第一个连接的点就是5，我要连接5！

3：我要和5匹配！泥奏凯！

2：好吧，那我连接的第二个点。。没有第二个点，我只有匹配5了！！！

3：我去，这么不凑巧，那好吧，我只好找找我连接的第二个点了，只有6了，6还没有被人占据，我捷足先登，嘿嘿嘿

4：我第一个连接的点是7，竟然被1占据了， 可恶，1给我等着，你去看看有没有别的边

1：我第一个连接的点是5，但是被2占据了，如果想让我给你挪腾地方的话，我只好先让2换个地方

2：那么我第一个连接的点是5，1你要用的话我就不可以匹配它。我没有第二个连接的点，因此1对不起，我不能给你挪腾地方

1：那好吧，那么我第二个连接的点是7——

4：我要这个点啊！本来我的目的就是让你挪腾地方离开7啊

1：那我没地可以挪腾了，爱能莫助啊~~~

4：那好吧，看看我连接的第二个点8，看来这个点没有被人占据，那么我就和它匹配

至此，所有的点都找到归属了。

（这tm不就是翻译过来吗，哪有正常人这么说话）

咳咳咳，anyway，匈牙利算法就是这样一个神奇的算法。

总结一下，从某种意义上来说，匈牙利算法算是一个动态规划。

为了读者理解方便，这里规定：我们枚举的点集用小写字母表示，另一个点集用大写字母表示。

因为由它的递归结构决定，只要一个点当前要匹配的点(设它为A)与另外的点(设它为B)要与同一个点(设它为c)匹配（为什么它们都要与c匹配的原因就是A是按照顺序依次匹配的，每一个A连接的点都要被依次尝试，由于匈牙利算法的内容决定的它的性质，因此无论顺序如何最后得到的都是最优的局面），那么A可以在B找到除了c以外的其它匹配的前提下达成对于A的最优局面，即A匹配c，B匹配另外的点。这样原来的匹配数不变，又增加了一条匹配。

如果B通过递归无法找到其它匹配，那么如果舍弃B这个匹配换上A的匹配，并不会增加匹配数。因此，这个策略是最优的。

但是这样说还不够，为什么就能保证A以前的匹配都是最优的呢？这样就必须说说B的递归匹配过程。

A要匹配c，那么让B与除了C以外的点匹配。如果B直接找到了未匹配的点（除了c，下同），那么直接匹配。如果B没有直接找到未匹配的点，那么B连接的边一定都是已经匹配其它点的。那么B就会尝试改变B要匹配的点(设它为d)的匹配的点(设它为E)的匹配，与A让B更换匹配一样，让E更换匹配为除了d以外的匹配点，这样B就可以得到d这个点的匹配了。然后，E重复B的过程......如此这般，如果一直找不到可以直接匹配的点的话，可以回溯到第一次匹配。这样，所有的匹配都会更换为：「在不改变原有匹配数的情况下，对A最优的局面，也就是对A匹配c最优的局面」，因此，每次匹配，总是会造成对当前局面的最优的匹配，如果局部不是最优，那么一旦涉及到需要这块局部最优的时候，这块将会同样被回溯到然后更改为最优。（这里的最优都是指的对当前局面的最优）。

当然，相信有聪明的同学已经想到，如果这样匹配的话，万一整个二分图不是联通图怎么办。很简单，如果按照上面代码的写法，每个连通块相当于一个二分图，每个二分图的匹配按照上面的写法总是最优的，最后的统计最大匹配只需要把每个连通块的最大匹配相加就可以了。

太长不看版：牵一发，动全身。每一次的尝试匹配的操作都会造成对当前整个图的匹配的调整，无论之前是怎样的图，最后都会被调整到对当前匹配最有利的图。

至于如何证明它的正确性，必须要这样一个东西来帮助我们：

增广路，它的性质是：（匹配点/边用1表示，非匹配点/边用0表示，N表示点/边的个数）

第一条边是非匹配边，然后到匹配边，然后到非匹配边......最后的边一定是非匹配边，并且边的个数一定是奇数。（01010101...0,N mod 2 ≠ 0）

那么匈牙利算法的实质，或者说另一种形式，就是不断寻找增广路来扩大匹配。

（我看的书上并没有增广路和匈牙利算法的关系，那么在这里详细说明是如何寻找增广路的）

在上面的描述中，我们知道，匈牙利算法的基本结构是枚举一个点集，通过上述方式“让”出最大匹配。

但是在“让”的过程中，我们发现，之前的操作，实际上都符合寻找增广路的方法。

例如，我们在匹配2的过程中（请回顾之前的模拟匈牙利算法的那段），

增广路的第一个点是2，接着经过那些操作，与2匹配的点是5，那么第二个点就是5。而之前与5匹配的点是1，1现在又7匹配。

则为：2->5->1->7

如果我们把更换匹配之前的匹配边称作匹配边，会发现：

2->5在更换匹配之前没有匹配，为非匹配边。

5->1在更换匹配之前是匹配的，为匹配边。

1->7在更换之前是没有匹配的，为非匹配边。

正好符合我们的增广路定义！其中，1->7就是我们增加的边。

为什么会这样?

让我们再来解说一次，用红色和蓝色来区分增广路和“让”的方法：

为了说明方便，这里假设最后匹配到了可以直接匹配的点，也就是说增广路发现成功

首先，增广路的第一个边必定是非匹配边。

我们枚举点集的时候必定没有枚举过当前枚举的点(设它为P)，那么P之前没有与任何边匹配，所以与P相连的边是非匹配边,设与P相连的点为i。

如果i原来不是匹配点，那么这条增广路已经结束，不存在第二条边，最后一条边是非匹配边。

然后，增广路的第二条边必定是匹配边，最后一条边必定是非匹配边。

同上，如果P连接的i原来不是匹配点，则增广路结束，第二条边不存在，而第一条边也是最后一条边，也符合定义。

如果i原来是匹配点，设X为i原来匹配的点，因为P为非匹配点，则X≠P，则X必定是这条增广路的第三个点，则这条边，也就是第二条边，是匹配边。

接着，增广路的第三条边必定是非匹配边

这儿分两种情况，第一是X更换到的点(设它为y)是非匹配点，可以直接匹配，那么因为y是非匹配点，则X->y是非匹配边，符合定义。

第二是y已经匹配了，由于X原来是匹配点，而一个点只能匹配一个点，X已经与i匹配，则y原来必定与X不匹配，则这条边(X->y)原来必定不是匹配边。符合定义。

...剩下同理

因此，只要最后找到了未匹配点，都算找到了增广路。

---------------------------

模板题HDU - 1083

#include <cstdio>
#include <cstring>

const int MaxN = ;

int ask[MaxN];
int vis[MaxN][MaxN];
int matched[MaxN];
int n,m;//n:课程人数，m:学生人数
int ans;

bool find(int from)
{
    for(int i = ; i <= m; i++){
        if(vis[from][i]){
            if(!ask[i]){
                ask[i] = ;

                if(!matched[i] || find (matched[i])){
                    matched[i] = from;
                    return ;
                }

            }

        }

    }
    return ;

}

void match(){
    int count = ;

    memset(matched,,sizeof(matched));

    for(int i = ; i <= n; i++){
        memset(ask,,sizeof(ask));

        if(find(i))
            count ++;

    }

    ans = count ;
}

int main()
{
    int data_p;
    scanf("%d",&data_p);
    while(data_p--){

    scanf("%d%d",&n,&m);

    for(int i = ; i <= m; i++){
        int num = ;

        scanf("%d",&num);
        for(int j = ; j <= num; j++){
            int tmp;
            scanf("%d",&tmp);
            vis[i][tmp] = ;

        }
    }

    match();

    if(ans == n){
        printf("YES\n");
    }
    else{
        printf("NO\n");
    }
    memset(vis,,sizeof(vis));
    ans = ;
    }

    return ;
}

先在match函数中枚举每个左集的点，每个左集的点调用Find函数。

Find中，枚举右集的点，找匹配，将匹配到的点标记，如果这个标记了的点没有被匹配或者递归上去能找到其他点匹配，那么就把当前点匹配。

最后，记录matched数组中的个数，即为最大匹配。

---------------------------

HDU - 3729

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>

const int MaxN = ;

struct EDGE{
    int to,nxt;
}edge[MaxN];
int head[];//[]点最后一个连接的边
int e_num;//边的数量 

void add(int u,int v){
    edge[++e_num].to = v;
    edge[e_num].nxt = head[u];

    head[u] = e_num;
}

int n,ans;
bool ask[MaxN];
int matched[MaxN];
int q[MaxN];

bool Find(int u){
    for(int i = head[u]; i ; i = edge[i].nxt){
        //if(edge[u][i]){
            if(!ask[edge[i].to]){
                ask[edge[i].to] = ;

                //printf("new : %d->%d\n",u,edge[i].to);

                if(!matched[edge[i].to] || Find(matched[edge[i].to])){
                    matched[edge[i].to] = u;
                    //printf("best match! %d|%d\n",u,i);

                    //printf("matched[%d] = %d\n",i,matched[i]);

                    return true;
                }
            }
        //}
    }

    return false;
}

void match(){
    memset(matched,,sizeof(matched));

    int count = ;

    for(int i = n; i >= ; i --){
        memset(ask,,sizeof(ask));
        if(Find(i))
            count ++;
    }

    ans = count;
}

int main()
{

    int data_n;
    scanf("%d",&data_n);
    while(data_n--){

        memset(edge,,sizeof(edge));
        memset(head,,sizeof(head));
        e_num = ;

    scanf("%d",&n);
    for(int i = ; i <= n; i++){
        int x1,x2;
        scanf("%d%d",&x1,&x2);
        for(int j = x1; j <= x2; j++){
            //edge[i][j] = 1;
            add(i,j);
        }
    }
    /*debug
    for(int  i = 1; i <= n; i++){
        for(int j = head[i] ; j ; j = edge[j].nxt){
            printf("%d - > %d\n",i,edge[j].to);

        }

    }
    //debug*/

    match();

    printf("%d\n",ans);

    int cnt = ;

    memset(q,,sizeof(q));

    for(int j = ; j <= ; j++){
        if(matched[j]){
            q[++cnt] = matched[j];
        }
    }

    std::sort(q+,q+cnt+);

    for(int j = ; j <= cnt; j++){
        printf("%d",q[j]);
        if(j != cnt)
            printf(" ");

        //printf("|end|");
    }

    //if(data_n != 0)
        printf("\n");

}

    return ;
}
/*
2
4
5004 5005
5005 5006
5004 5006
5004 5006
7
4 5
2 3
1 2
2 2
4 4
2 3
3 4
*/

几乎是模板题，只不过数据有10万，并且需要最大字典序输出，只需要把之前的邻接矩阵改成邻接表即可提高速度，

只要把左集倒序枚举即可得到最大字典序答案。

---

窃以为理解透彻了，将思路全部放上来，可能有些啰嗦。

写到后面脑子很乱，不知道该如何表达，不对地方还请指正