杭电2602 Bone Collector

Bone Collector

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 65099    Accepted Submission(s): 27122

Problem Description

Many years ago , in Teddy’s hometown there was a man who was called “Bone Collector”. This man like to collect varies of bones , such as dog’s , cow’s , also he went to the grave …
The bone collector had a big bag with a volume of V ,and along his trip of collecting there are a lot of bones , obviously , different bone has different value and different volume, now given the each bone’s value along his trip , can you calculate out the maximum of the total value the bone collector can get ?

 

Input

The first line contain a integer T , the number of cases.
Followed by T cases , each case three lines , the first line contain two integer N , V, (N <= 1000 , V <= 1000 )representing the number of bones and the volume of his bag. And the second line contain N integers representing the value of each bone. The third line contain N integers representing the volume of each bone.

 

Output

One integer per line representing the maximum of the total value (this number will be less than 2³¹).

 

Sample Input

1
5 10
1 2 3 4 5
5 4 3 2 1

 

Sample Output

14

 

题目大意：有一个骨头收集者，他有一个容量为V的包，他要收集N根骨头，每根骨头拥有它的价值Valu和占用体积Vol，求最优解。

 

这是个简单的01背包问题，核心算法就是：F[i,v] = max{F[i − 1,v],F[i − 1,v − C i ] + W i } 具体的解释请看我的另一片博文：http://www.cnblogs.com/William-xh/p/7305877.html

 

主要就是还是要进行判断，如果背包放得下的话，那就是要看我放还是不放；如果是放不下的话，那就是不放。

 

这题我是用二维数组解的，一位数组那个代码还没有研究过，就也还没写过。之后要是写的话就码上来。

附上代码：

#include <iostream>
#include<math.h>
#include <iomanip>
#include<cstdio>
#include<string>
#include<map>
#include<vector>
#include<list>
#include<algorithm>
#include<stdlib.h>
#include<iterator>
#include<sstream>
#include<string.h>
#include<stdio.h>
using namespace std;
int dp[][];

int max(int x,int y)
{
    return x>y?x:y;
}

int main()
{
   int t;
   cin>>t;
   int n,v;
   int vol[],value[];
   while(t--)
   {
       cin>>n>>v;//记录骨头数量和总体积
       for(int iii=;iii<=n;iii++)
       {
           cin>>value[iii];//记录值
       }
       for(int ii=;ii<=n;ii++)
       {
           cin>>vol[ii];//记录体积
       }
       memset(dp,,sizeof(dp));//把背包初始化为所有的情况价值都为0

        for(int i=;i<=n;i++)//有几件物品
        {
            for(int j=;j<=v;j++)//表示有几件物品时，你的背包容量在变化的同时，你背包的总价值是否发生了变化
            {
                if(vol[i]<=j)//当你的背包放得下第i件物品时
                {//就要考虑两种情况 1.放这件物品，也就是为这件物品腾出空间，然后计算剩下的空间放I-1件物品的最大值，这时候背包的价值=dp[i-1][j-vol[i]]+valu[i]
                 //2.不放这件物品，就是只考虑在这样的容量下，放i-1件物品的情况。这时候 背包的价值为： dp[i-1][j]
                 //所以我们就要比较他们的最大值
                 dp[i][j]=max(dp[i-][j],dp[i-][j-vol[i]]+value[i]);
                }
                else{//当放不下这件物品的时候(要是只有一个公式的话 ij 可能会负)
                    dp[i][j]=dp[i-][j];
                }

            }
        }
        cout<<dp[n][v]<<endl;
   }
    return ;
}

然后在此进行一位数组的解释，这边有一个讲的还是比较清楚的：http://blog.csdn.net/qq_32036091/article/details/51301912

一维数组优化

且说小Ho搞清楚了计算方法，正在埋头苦写代码，在一旁看他写代码的小Hi是在看不下去了，决定再指点指点小Ho：“小Ho啊！”

“怎么了？”小Ho眼睛盯着屏幕，望都没望小Hi一眼。

“你现在是不是需要开一个N * M大小的二维数组best，来记录求解出的best值呀？”

小Ho终于有了点反应，抬起头来说道：“是啊，怎么了？“

“我有办法不用开这么大空间哦~”小Hi笑嘻嘻道：”可我就是不告诉你！”

“诶，别这样，我请你吃雪糕！”小Ho一听就急了，连忙许下了报酬。

“开玩笑啦~”小Hi也是随便逗了逗乐子就没继续：“你想想，在i已经是10以上的时候，best(5, j)这样的值还有用么？”

“没有用了……你是说，我并不需要在内存中存下来所有的best(i, j)，没有用了的值都可以不进行保存……也就是说，实际上只要开一个2*M大小的数组就可以了，然后像这样的方式进行来回的计算，是不是就可以了？”

“是的呢！但是还可以更少哦~让我来写这个程序的话，我只需要开一个M大小的一维数组就可以了”小Hi自信的说道：“你想想，如果我按照j从M到1的顺序，也就是跟之前相反的顺序来进行计算的话。另外根据我们的状态转移方程，可以显然得出如果状态(iA, jA)依赖于状态(iB, jB)，那么肯定有iA = iB+1, jA>=jB。所以不难得出一个结论：我在计算best(i, j)的时候，因为best(i, j+1..M)这些状态已经被计算过了，所以意味着best(i - 1, k)，k=j..M这些值都没有用了——所有依赖于他们的值都已经计算完了。于是它们原有的存储空间都可以用来存储别的东西，所以我不仿直接就将best(i, j)的值存在best(i-1, j)原有的位置上，就像这样。”

“原来还可以这样！这样一处理，不仅空间复杂度小了很多，代码也很好看了呢！”小Ho开心道。

“那你还不去写？”

然后，我在这边附一张自己的演示图：

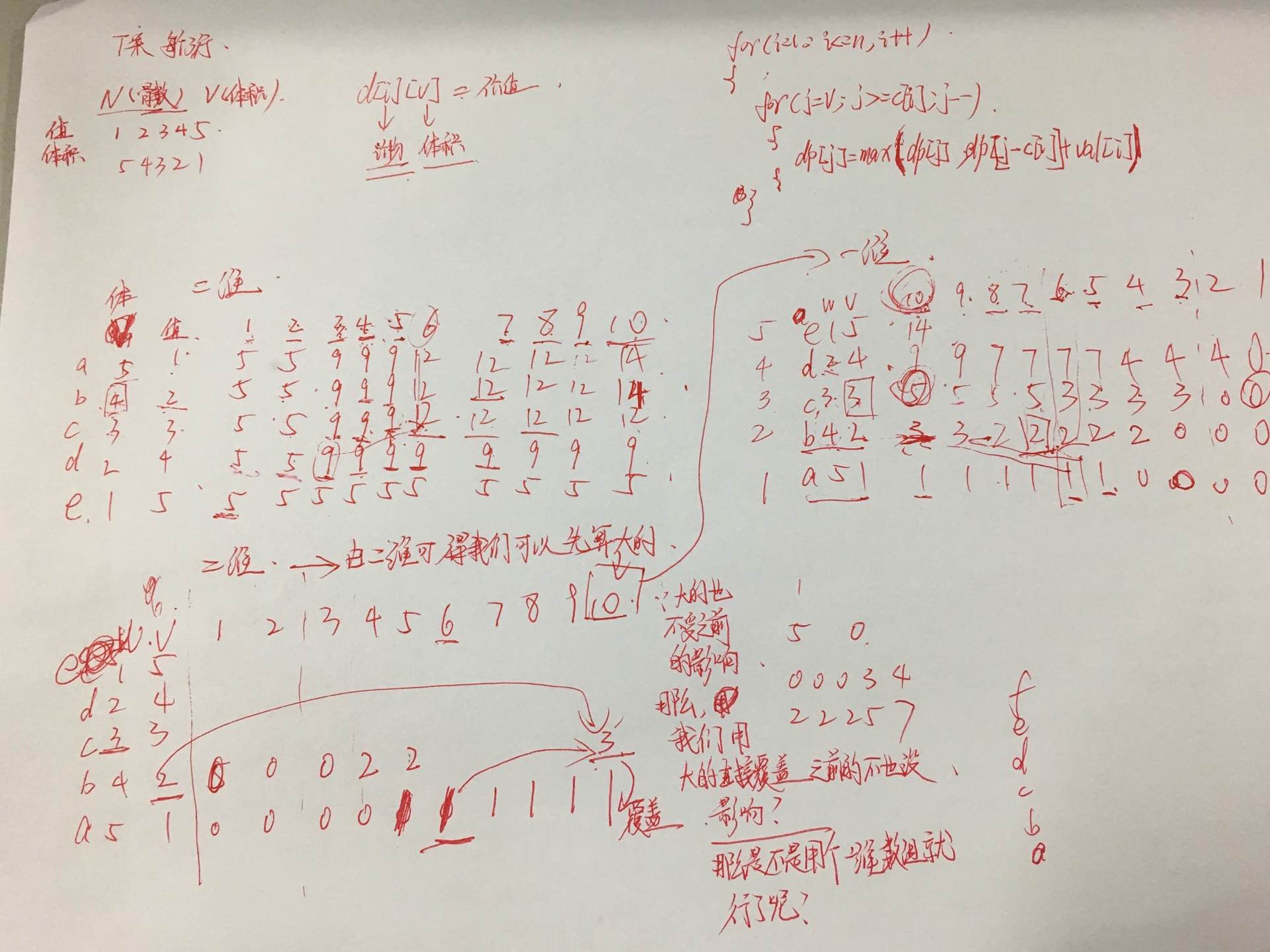
然后，根据你在纸上换算的过程，你可以得到一个核心算法：dp[j]=max(dp[j],dp[j-vol[i]]+value[i]);

其实一维数组的核心就在于：1.从大到小进行计算   2.对之前的数据进行覆盖。

然后附上代码：

#include <iostream>
#include<math.h>
#include <iomanip>
#include<cstdio>
#include<string>
#include<map>
#include<vector>
#include<list>
#include<algorithm>
#include<stdlib.h>
#include<iterator>
#include<sstream>
#include<string.h>
#include<stdio.h>
using namespace std;

int max(int x,int y)
{
    return x>y?x:y;
}

int main()
{
   int t;
   cin>>t;
   int n,v;
   int vol[],value[], dp[];;
   while(t--)
   {
       cin>>n>>v;//记录骨头数量和总体积
       for(int iii=;iii<=n;iii++)
       {
           cin>>value[iii];//记录值
       }
       for(int ii=;ii<=n;ii++)
       {
           cin>>vol[ii];//记录体积
       }
       memset(dp,,sizeof(dp));//把背包初始化为所有的情况价值都为0

        for(int i=;i<=n;i++)
        {
            for(int j=v;j>=vol[i];j--)
            {//因为根据状态方程的那个表，我们倒着来算依然没有问题
                //而且，倒着算的话，因为我们是先算大的dp[i][j]，那么后面小dp[i][j-m]的不会用到之前的dp[i-1][j]
                //所以我们可以用dp[i][j]直接覆盖掉之前的dp[i-1][j]，那么只用一维数组即可
                dp[j]=max(dp[j],dp[j-vol[i]]+value[i]);
            }
        }
        cout<<dp[v]<<endl;
  }
   return ;
}