java-信息安全（九）-基于DH,非对称加密，对称加密等理解HTTPS

概述

java-信息安全（七）-基于非对称加密，对称加密等理解HTTPS

如果想要理解好https，请尽量了解好以上信息等。

参看文章：

http://www.ruanyifeng.com/blog/2014/09/illustration-ssl.html

https://cattail.me/tech/2015/11/30/how-https-works.html

基本概念

　　客户端和服务端在握手hello消息中明文交换了client_random和server_random ，使用RSA公钥加密传输premaster secret ，最后通过算法，客户端和服务端分别计算master secret。其中，不直接使用premaster secret 的原因是：保证secret的随机性不受任意一方的影响。

　　整个握手阶段都不加密（也没法加密），都是明文的。因此，如果有人窃听通信，他可以知道双方选择的加密方法，以及三个随机数中的两个。整个通话的安全，只取决于第三个随机数（Premaster secret）能不能被破解。

　　虽然理论上，只要服务器的公钥足够长（比如2048位），那么Premaster secret可以保证不被破解。但是为了足够安全，我们可以考虑把握手阶段的算法从默认的RSA算法，改为 Diffie-Hellman算法（简称DH算法）。

　　采用DH算法后，Premaster secret不需要传递，双方只要交换各自的参数，就可以算出这个随机数。

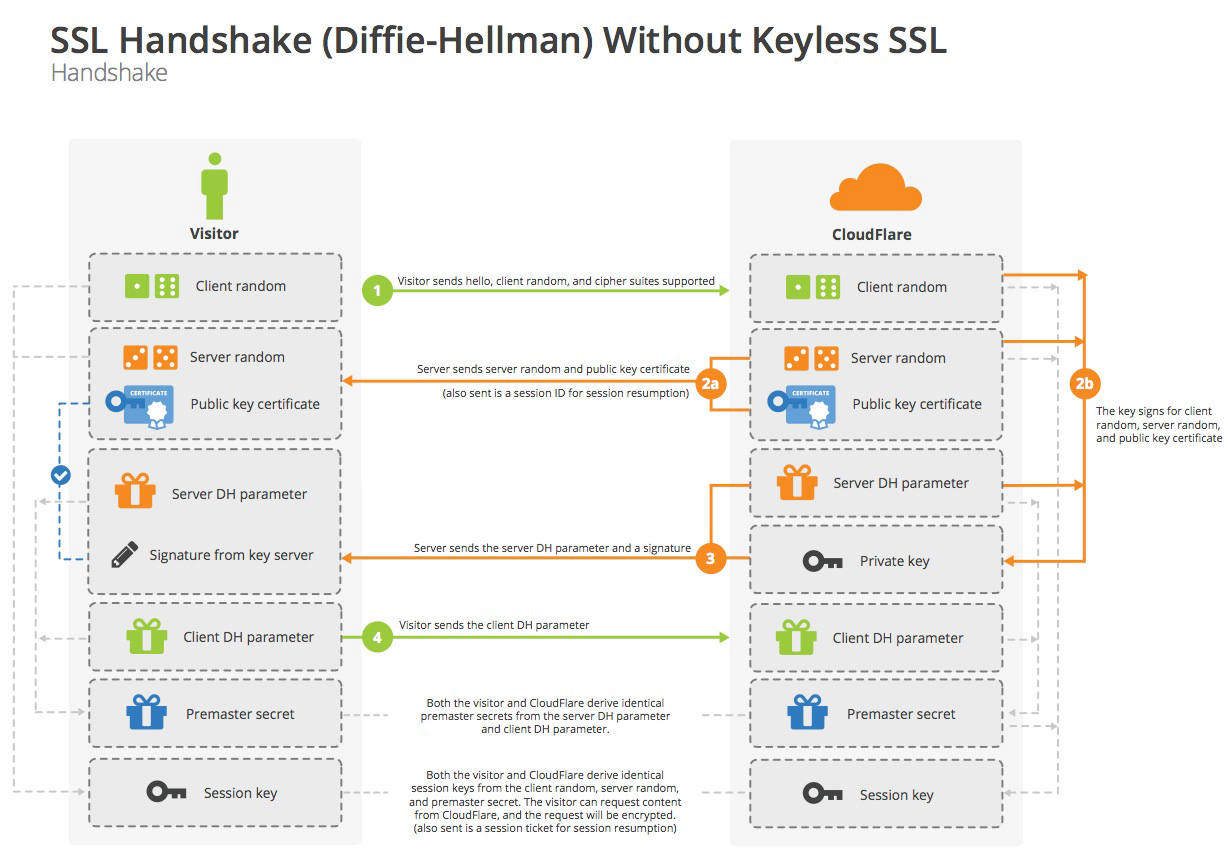
　　上图中，第三步和第四步由传递Premaster secret变成了传递DH算法所需的参数，然后双方各自算出Premaster secret。这样就提高了安全性。