RSA 理论

一、同余

给定一个正整数m，如果两个整数a和b满足（a-b）能够被m整除，即（a-b）/m得到一个整数，那么就称整数a与b对模m同余，记作a≡b(mod m)

二、欧拉定理

任意给定正整数n，请问在小于等于n的正整数之中，有多少个与n构成互质关系？

计算这个值的方法就叫做欧拉函数，以φ(n)表示。

在1到8之中，与8形成互质关系的是1、3、5、7，所以 φ(8) = 4。

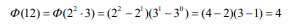
a的φ(n)次方被n除的余数为1。或者说，a的φ(n)次方减去1，可以被n整除。

比如，

3和7互质，而7的欧拉函数φ(7)等于6，所以3的6次方减去1，可以被7整除（即：（729-1）/ 7 = 104）。

比如，

5和12互质

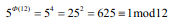
如果两个正整数a和n互质，则n的欧拉函数 φ(n) 可以让下面的等式成立：

欧拉定理可以大大简化某些运算。比如，7的222次方的个位数

7和10互质，根据欧拉定理，

已知 φ(10) = 4，所以马上得到7的4倍数次方的个位数肯定是1。

欧拉定理有一个特殊情况（费马小定理）。

假设正整数a与质数p互质，如果质数p的φ(p)等于p-1，则欧拉定理可以写成

三、模反

如果两个正整数a和n互质，那么一定可以找到整数b，使得 ab-1 被n整除，或者说ab被n除的余数是1。

这时，b就叫做a的"模反元素"。

比如，3和11互质，那么3的模反元素就是4，因为 (3 × 4)-1 可以被11整除。

显然，模反元素不止一个， 4加减11的整数倍都是3的模反元素 {...,-18,-7,4,15,26,...}，即如果b是a的模反元素，则 b+kn 都是a的模反元素。

欧拉定理可以用来证明模反元素必然存在。

可以看到，a的 φ(n)-1 次方，就是a的模反元素。

四、加密过程

第一步，随机选择两个不相等的质数p和q ： 61和53。

第二步，计算p和q的乘积n。 n = 61×53 = 3233

n的长度就是密钥长度。3233写成二进制是110010100001，一共有12位，所以这个密钥就是12位。

实际应用中，RSA密钥一般是1024位，重要场合则为2048位。

第三步，计算n的欧拉函数φ(n)。

根据公式：φ(n) = (p-1)(q-1)

φ(3233)=60×52=3120。

第四步，随机选择一个整数e，条件是1< e < φ(n)，且e与φ(n) 互质。

随机选择了17。（实际应用中，常常选择65537。）

第五步，计算e对于φ(n)的模反元素d。

所谓"模反元素"就是指有一个整数d，可以使得ed被φ(n)除的余数为1。

　　ed ≡ 1 (mod φ(n))

这个式子等价于

　　ed - 1 = kφ(n)

于是，找到模反元素d，实质上就是对下面这个二元一次方程求解。

　　ex + φ(n)y = 1

已知 e=17, φ(n)=3120，

　　17x + 3120y = 1

算出一组整数解为 (x,y)=(2753,-15)，即 d=2753。

至此所有计算完成。

第六步，将n和e封装成公钥，n和d封装成私钥。

n=3233，e=17，d=2753，所以公钥就是 (3233,17)，私钥就是（3233, 2753）。

实际应用中，公钥和私钥的数据都采用ASN.1格式表达（实例）。

参考：

阮一峰：RSA算法原理