paper 112：hellinger distance

在概率论和统计理论中，Hellinger距离被用来度量两个概率分布的相似度。它是f散度的一种（f散度——度量两个概率分布相似度的指标）。Hellinger距离被定义成Hellinger积分的形式，这种形式由Ernst Hellinger在1909年引进。

目录

·1 定义

·1.1 度量理论

·1.2 基于Lebesgue度量的概率理论

·1.3 离散概率分布

·2 性质

·3 例子

1 定义

1.1 度量理论

为了从度量理论的角度定义Hellinger距离，我们假设P和Q是两个概率测度，并且它们对于第三个概率测度λ来说是绝对连续的，则P和Q的Hellinger距离的平方被定义如下：

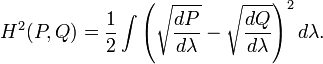
这里的dP / dλ 和 dQ / dλ分别是P和Q的Radon–Nikodym微分。这里的定义是与λ无关的，因此当我们用另外一个概率测度替换λ时，只要P和Q关于它绝对连续，那么上式就不变。为了简单起见，我们通常把上式改写为：

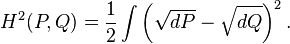
1.2 基于Lebesgue度量的概率理论

为了在经典的概率论框架下定义Hellinger距离，我们通常将λ定义为Lebesgue度量，此时dP / dλ 和 dQ / dλ就变为了我们通常所说的概率密度函数。如果我们把上述概率密度函数分别表示为 f 和 g ，那么可以用以下的积分形式表示Hellinger距离：

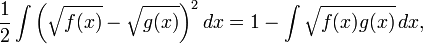
上述等式可以通过展开平方项得到，注意到任何概率密度函数在其定义域上的积分为1。

根据柯西-施瓦茨不等式（Cauchy-Schwarz inequality），Hellinger距离满足如下性质：

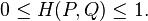
1.3 离散概率分布

对于两个离散概率分布 P=(p1,p2,...,pn)和 Q=（q1,q2,...,qn)，它们的Hellinger距离可以定义如下：

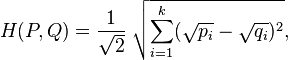
上式可以被看作两个离散概率分布平方根向量的欧式距离，如下所示：

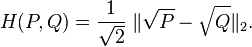
2. 性质

Hellinger距离的最大值1只有在如下情况下才会得到：P在Q为零的时候是非零值，而在Q为非零值的时候是零，反之亦然。

有时公式之前的系数1/2会被省略，此时Hellinger距离的范围变为从0到2的平方根。

Hellinger距离可以跟Bhattacharyya系数BC(P,Q)联系起来，此时它可以被定义为：

Hellinger距离通常在顺序和渐进统计中使用。

3. 例子

两个正态分布P 和 Q的Hellinger距离的平方可以被定义为：

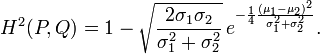
两个指数分布P 和 Q的Hellinger距离的平方可被定义为：

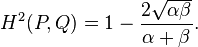
两个威利分布P 和 Q（此处k是一个形状参数，α和β是尺度系数）的Hellinger距离的平方可被定义为：

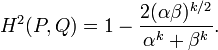
对于两个具有参数α和β的泊松分布 P 和 Q，它们的Hellinger距离可被定义为：

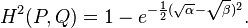
上述内容来自wikipedia

http://en.wikipedia.org/wiki/Hellinger_distance#mw-head