Matrix 矩阵 那么什么是矩阵呢？

矩阵可以理解为方阵，只不过 平时方阵里面站着人 矩阵中是数值：

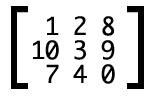
CSS3中的矩阵：

css3中的矩阵指的是一个方法，书写为matrix() 和 matrix3d(),前者是元素2D平面的移动变换(transfrom)，而后者是3D变换。2D变换矩阵3*3，如上图的示意图：3D变换则是4*4的矩阵。

可能有些难以理解 我们可以先看看其他东西 层层渐近-transform属性

.trans_skew { transform: skew(35deg); }

.trans_scale { transform:scale(1, 0.5); }

.trans_rotate { transform:rotate(45deg); }

.trans_translate { transform:translate(10px, 20px); }

扭曲（skew）缩放(scale) 旋转(rotate) 以及位移(translate)

那你有没有想过 为什么transform：rotate(45deg); 会让元素旋转45度 其后面作用的机理是什么呢。

下面这张图可以解释上面的疑问：

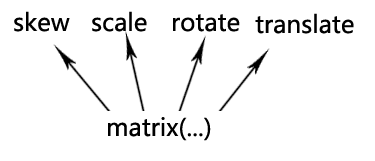
可以看到无论是旋转还是拉伸 本质上应用的都是matrix()方法实现的(修改matrix()方法固定的几个值)，只是类似于transform:rotate这种表现形式 我们更容易理解 记忆 与 上手。

换句话说理解transform中的matrix()矩阵方法有利于透彻理解CSS3中的transform属性。

矩阵应用场景和transform的坐标系统

实际上 在CSS3以及HTML5的世界里 矩阵matrix用的还是十分广泛的。 如 SVG和canvas

用过transform旋转的人可能发现了 其默认是绕着中心点旋转的，而这个中心点就是transform-origin属性对应的点。也就是矩阵计算的一个重要的依据点。

当我们通过transform-origin属性进行设置的时候，矩阵相关的计算也就随着而改变，反映到实际图像效果上就是 旋转拉伸的中心点变了！

举例来说：如果我们设置了元素的基点在左下角时：

-webkit-transform-origin: bottom left;

坐标中心就是左下角位置  于是动画(比如图片收缩)就是基于图片的左下角这一点了：

<head>

        <meta charset="UTF-8">

        <title></title>

        <style type="text/css">

            .anim_image {

                -webkit-transition: all 1s ease-in-out;

                -moz-transition: all 1s ease-in-out;

                transition: all 1s ease-in-out;

                cursor: pointer;

            }

            .anim_image_top {

                position: absolute;

                -webkit-transform: scale(0,0);

                opacity: 0;

            }

            .anim_box:hover .anim_image_top  {

                opacity: 1;

                -webkit-transform: scale(1,1);

                -webkit-transform-origin:top right;

            }

            .anim_box:hover .anim_image_bottom {

                    -webkit-transform: scale(0, 0);

                    -webkit-transform-origin: bottom left;

            }

        </style>

    </head>

    <body>

        <div id="testBox" class="demo anim_box">

            <img class="anim_image anim_image_top" src="../img/top.png" />

                <img class="anim_image anim_image_bottom" src="../img/bottom.png" />

        </div>

    </body>

</html>

可以运行一下 看看效果 分别是基于右上角 和 左上角的缩放。

可以在举个例子

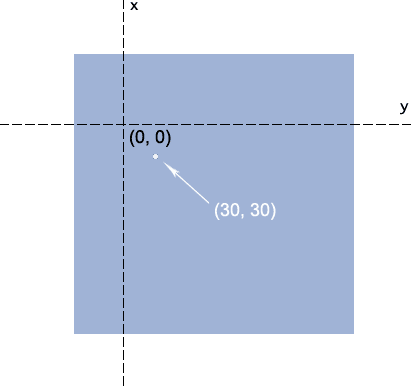
transform-origin: 50px 70px;

中心点的位置移到了距离左侧50像素 顶部70像素的地方 而此时的(30,30)坐标则移到了图中白点的位置：

现在是不是很好理解了呢。

下面我们就跟着大神的脚步 来理解一下 2D matrix (哈哈 我也是看着大神的博客抄的。后面会贴出出处)

CSS3中 transform的matrix()方法 写法如下：

transform:matrix(a,b,c,d,e,f);

参数很复杂 达到了六个

实际上这六个参数对应的矩阵就是：

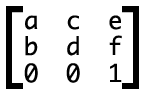
注意书写的方向是竖着的。

上面提过，矩阵可以想象成古代的士兵方阵，要让其发生变化，只有与另外一个士兵阵火拼就可以了，即使这是个小阵。

反应到这里 就是如下的转换公式

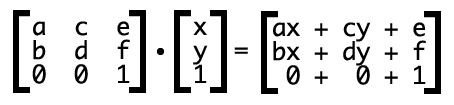
其中 x,y表示转换元素的所有坐标了 那后面的ax＋cy＋e是怎么来的呢？

很简单 3*3矩阵每一行的第一个值与后面1*3的第一个值相乘

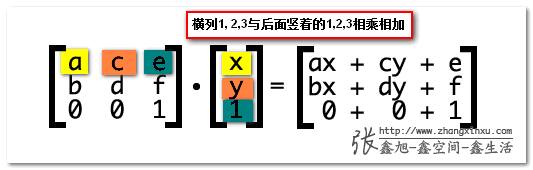
那ax+cy+e的意义是什么？

记住了，ax+cy+e为变换后的水平坐标，bx+dy+f表示变换后的垂直位置。

下面看一个例子：

transform: matrix(1, 0, 0, 1, 30, 30); /* a=1, b=0, c=0, d=1, e=30, f=30 */

现在 我们根据这个矩阵偏移元素的中心点，假设是(0,0)，即x=0 y = 0

于是，变换后的x坐标就是ax+cy+e = 1*0+0*0+30 =30, y坐标就是bx+dy+f = 0*0+1*0+30 =30.

于是，中心点坐标从(0, 0)变成了→(30, 30)。对照上面有个(30, 30)的白点图，好好想象下，原来(0,0)的位置，移到了白点的(30, 30)处，怎么样，是不是往右下方同时偏移了30像素哈！！

实际上transform: matrix(1, 0, 0, 1, 30, 30);就等同于transform: translate(30px, 30px);. 注意：translate, rotate等方法都是需要单位的，而matrix方法e, f参数的单位可以省略。

所以说 可以看出来 只要是中心点没有改变还是原来的(0,0) 那么matrix表现偏移就是

transform: matrix(与我无关, 哪位, 怎么不去高考, 打麻将去吧, 水平偏移距离, 垂直偏移距离);

你只要关心后面两个参数就可以了，至于前面4个参数，是牛是马，是男是女都没有关系的。

transform matrix矩阵与缩放，旋转以及拉伸

偏移是matrix效果中最简单，最容易理解的，因此，上面很详尽地对此进行展开说明。下面，为了进一步加深对matrix的理解，会简单讲下matrix矩阵与缩放，旋转以及拉伸效果。

缩放(scale)
上面的偏移只要关心最后两个参数，这个缩放也是只要关心两个参数。哪两个呢？

如果你足够明察秋毫，应该已经知道了，因为上面多次出现的：

transform: matrix(1, 0, 0, 1, 30, 30);

已经出卖了。

发现没，matrix(1, 0, 0, 1, 30, 30);的元素比例与原来一样，1:1, 而这几个参数中，有两个1, 啊哈哈！没错，这两个1就是缩放相关的参数。

其中，第一个缩放x轴，第二个缩放y轴。

用公式就很明白了，假设比例是s，则有matrix(s, 0, 0, s, 0, 0);，于是，套用公式，就有：
x' = ax+cy+e = s*x+0*y+0 = s*x;
y' = bx+dy+f = 0*x+s*y+0 = s*y;

也就是matrix(sx, 0, 0, sy, 0, 0);，等同于scale(sx, sy);

旋转(rotate)
旋转相比前面两个要更高级些，要用到（可能勾起学生时代阴影的）三角函数。

方法以及参数使用如下（假设角度为θ）：

matrix(cosθ,sinθ,-sinθ,cosθ,0,0)

结合矩阵公式，就有：

x' = x*cosθ-y*sinθ+0 = x*cosθ-y*sinθ

y' = x*sinθ+y*cosθ+0 = x*sinθ+y*cosθ

哎呀呀，四个参数，我记不住啊！莫慌，我们可以这样子记忆：
CS-SC：初三-上床，对称结构，这下忘不了了吧~~

不过，说句老实话，就旋转而言，rotate(θdeg)这种书写形式要比matrix简单多了，首先记忆简单，其次，无需计算。例如，旋转30°，前者直接：

transform:rotate(30deg);

而使用matrix表示则还要计算cos, sin值：

transform: matrix(0.866025,0.500000,-0.500000,0.866025,0,0);

拉伸(skew)
拉伸也用到了三角函数，不过是tanθ，而且，其至于b, c两个参数相关，书写如下（注意y轴倾斜角度在前）：

matrix(1,tan(θy),tan(θx),1,0,0)

套用矩阵公式计算结果为：

x' = x+y*tan(θx)+0 = x+y*tan(θx)

y' = x*tan(θy)+y+0 = x*tan(θy)+y

对应于skew(θx + "deg"，θy+ "deg")这种写法。

其中，θx表示x轴倾斜的角度，θy表示y轴，两者并无关联。

大神的博客在此 有兴趣的可以移步到此：http://www.zhangxinxu.com/wordpress/2012/06/css3-transform-matrix-矩阵/

HTML 学习笔记 CSS3 (2D Matrix)的更多相关文章

  1. HTML 学习笔记 CSS3 (2D转换)

    2.scaleX(<number>) : 使用 [sx,1] 缩放矢量执行缩放操作,sx为所需参数.scaleX表示元素只在X轴(水平方向)缩放元素,他的默认值是(1,1),其基点一样是在 ...

  2. A.Kaw矩阵代数初步学习笔记 4. Unary Matrix Operations

    “矩阵代数初步”(Introduction to MATRIX ALGEBRA)课程由Prof. A.K.Kaw(University of South Florida)设计并讲授. PDF格式学习笔 ...

  3. A.Kaw矩阵代数初步学习笔记 3. Binary Matrix Operations

    “矩阵代数初步”(Introduction to MATRIX ALGEBRA)课程由Prof. A.K.Kaw(University of South Florida)设计并讲授. PDF格式学习笔 ...

  4. css3学习笔记之2D转换

    translate() 方法 translate()方法,根据左(X轴)和顶部(Y轴)位置给定的参数,从当前元素位置移动. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 ...

  5. HTML 学习笔记 CSS3(Animation)

    CSS3动画: 通过CSS3 我们能够创建动画 这可以在许多网页中取代动画图片 Flash动画 以及JavaScript. CSS3 @keyframes 规则如需在 CSS3 中创建动画,您需要学习 ...

  6. HTML 学习笔记 CSS3(过度 transition)

    通过 CSS3,我们可以在不使用 Flash 动画或 JavaScript 的情况下,当元素从一种样式变换为另一种样式时为元素添加效果.请把鼠标移动到下面的元素上: 先看一下这个代码 实现旋转放大的效 ...

  7. ArcGIS API for JavaScript 4.2学习笔记[10] 2D添加指北针widget、视图保存、视图padding（第二章完结）

    这几个例子是第二章除了入门之外比较简单的几个,就做个合集,把最核心的代码(第二参数)和 引用放上来即可,不作多解释. 2D地图添加指北针widget 2D地图一般修正方向为正北方就需要这个widget ...

  8. 前端学习笔记--CSS3

    本本记录了css3的样式:浏览器支持度.圆角边框.阴影.文字与文本.过渡.动画.2d旋转.3d旋转 浏览器支持度: 1.圆角边框 例:只要确定了x.y值,就能知道弧度 画一个圆形:长=宽,border ...

  9. HTML 学习笔记 CSS3 (多列)

    CSS3多列 通过CSS3 我们能够创建多个列来对文本进行布局. 在这篇文章中 你将了解到如下多列属性: column-count column-gap column-rule 浏览器支持: 多列的属 ...

随机推荐

  1. Microsoft Azure 的负载平衡器的Session Sticky

    Microsoft Azure 的负载平衡器是一种 Layer-4负载平衡器.Microsoft Azure 负载平衡器通过针对给定输入端点上接收到的流量计算哈希函数,在一组可用的服务器(虚拟机)之间 ...

  2. vbs操作excel

    航天金税系统升级,导出的Excel文件格式与原来有的差异,老的数据导入程序识别不了该文件,对比了新老文件后,发现新文件在专票和普票的“份数”行前增加了一行,同时增加了“单据号”列,通过脚本 把这些删除 ...

  3. Android 国际化

    由于公司的项目是投放 google play store , 所以要做国际化.国际化遇到的两个大问题 字符串国际化 布局样式国际化 一:字符串国际化        解决这个问题很简单,在res目录下放 ...

  4. 【代码笔记】iOS-等待动画

    一,效果图. 二,工程图. 三,代码. RootViewController.h #import <UIKit/UIKit.h> @interface RootViewController ...

  5. 【读书笔记】iOS网络-理解错误源

    考虑一个字节是如何从设备发往运程服务器以及如何从远程服务器将这个字节接收到设备,这个过程只需要几百毫秒时间,不过确要求网络设备都能正常工作才行.设备网络和网络互联的复杂性导致了分层网络的产生.分层网络 ...

  6. android 界面设计基本知识Ⅲ

    本章继续讲述在android界面设计中相关的知识点.介绍内容包括BroadcastReceiver(广播),Service(服务),Widget(小部件),WebView(网页加载控件). 1.Bro ...

  7. Cookie/Session机制

    这些都是基础知识,不过有必要做深入了解.先简单介绍一下. 二者的定义: 当你在浏览网站的时候,WEB 服务器会先送一小小资料放在你的计算机上,Cookie 会帮你在网站上所打的文字或是一些选择, 都纪 ...

  8. (视频) 基于HTML5的服务器远程访问工具

    现在云计算这么发达,基本上每个人都多少有几台Windows或者Linux服务器运行在云端,要直接进入这些服务器进行配置就需要使用类似远程桌面或者Putty这类的工具,虽然大多数Windows电脑都自带 ...

  9. PreferenceScreen监听子项的刷新

    有个PreferenceScreen,他有一些个子项目.它的Summary需要根据子项的设置来改变的,所以需要监听子项的刷新事件. preferenceScreen.setOnPreferenceCh ...

  10. Windows Server 2012 Recycle Bin corrupted

    在Windows Server 2012 上遇到了“The Recycle Bin On E:\ is corrupted. Do you want to empty the Recycle Bin ...