AVL树插入操作实现

为了提高二插排序树的性能，规定树中的每个节点的左子树和右子树高度差的绝对值不能大于1。为了满足上面的要求需要在插入完成后对树进行调整。下面介绍各个调整方式。

右单旋转

如下图所示，节点A的平衡因子(左子树高度减右子树高度)为1。由于在节点A的左孩子B的左子树上插入了新节点，导致B的左子树高度增加1，从而导致A的平衡因子为2，这时为了保持平衡需要对树进行调整。

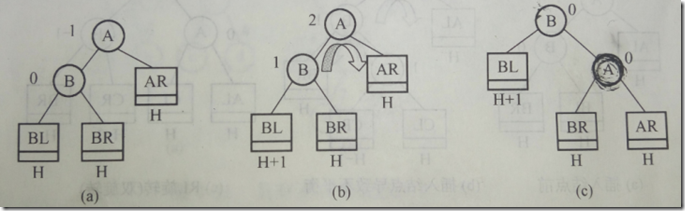
旋转的方法就是将A的变为B的右子树，将B的右子树变为A的左子树。

示例代码：

private Node RRotate(Node node){
    Node A </span>=<span style="color: #000000"> node;

    Node B </span>=<span style="color: #000000"> node.LChild;

    </span><span style="color: #008000">//</span><span style="color: #008000">旋转</span>

    Node tmp =<span style="color: #000000"> B.RChild;

    B.RChild </span>=<span style="color: #000000"> A;

    A.LChild </span>=<span style="color: #000000"> tmp;

    </span><span style="color: #008000">//</span><span style="color: #008000">更新树的高度</span>

    A.height = Math.max(height(A.LChild), height(A.RChild))+1<span style="color: #000000">;

    B.height </span>= Math.max(height(B.LChild), height(B.RChild))+1<span style="color: #000000">;

    </span><span style="color: #0000ff">return</span><span style="color: #000000"> B;

}</span></pre></div>


（每个节点我们维护了一个height的属性来记录树的高度，每次旋转完成后需要更新树的高度。因为旋转会导致书的根节点发生变化，所以每次旋转完成后需要将新的根节点返回）
左单旋转

左单旋转整好与右单旋转相反。右单旋转是因为左子树太高，而左单旋转则是因为右子树太高，需要降低其高度。
如图所示节点B的右子树高度增加1，导致节点A的平衡因子变为-2，所以需要进行左旋调整位置。

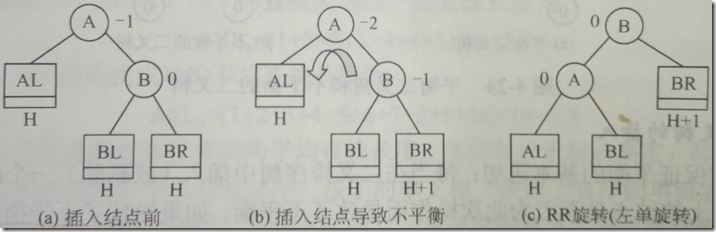
旋转方法：将A变为B的左子树，将B的左子树变为A的右子树
示例代码：

private Node LRotate(Node node){

        Node A = node;

        Node B = node.RChild;
    </span><span style="color: #008000">//</span><span style="color: #008000">旋转</span>

    Node tmp =<span style="color: #000000"> B.LChild;

    B.LChild </span>=<span style="color: #000000"> A;

    A.RChild </span>=<span style="color: #000000"> tmp;

    </span><span style="color: #008000">//</span><span style="color: #008000">更新树的高度</span>

    A.height = Math.max(height(A.LChild), height(A.RChild))+1<span style="color: #000000">;

    B.height </span>= Math.max(height(B.LChild), height(B.RChild))+1<span style="color: #000000">;

    </span><span style="color: #0000ff">return</span><span style="color: #000000"> B;

}</span></pre></div>


（每个节点我们维护了一个height的属性来记录树的高度，每次旋转完成后需要更新树的高度。因为旋转会导致书的根节点发生变化，所以每次旋转完成后需要将新的根节点返回）
先左后右旋转

上面的两种情况处理比较简单，因为插入的节点要么是根节点左孩子的左子树或者是根节点右孩子的右子树。如果插入的节点在根节点左孩子的右子树上，则需要先进行左旋然后进行右旋操作。

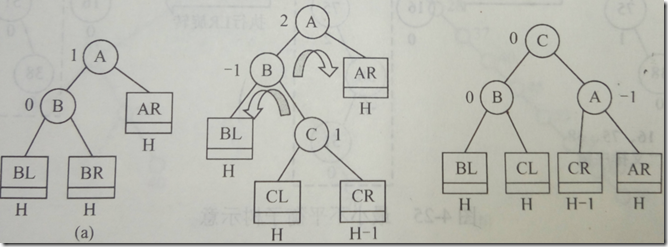
如图所示，插入的节点在B节点右子树上，这时需要对B节点进行左旋操作，然后对A节点进行右旋操作。
示例代码：

private Node LRRotate(Node node){

        //先进行左旋

        LRotate(node.LChild);

        //在进行右旋

        return RRotate(node);

    }

代码中node节点就是图中的A节点，先对A节点的左孩子B进行左旋操作，然后对A(node)节点进行右旋操作
先右旋后左旋

当插入的节点在根节点的右孩子的左子树上，则需要进行先右旋后左旋操作。

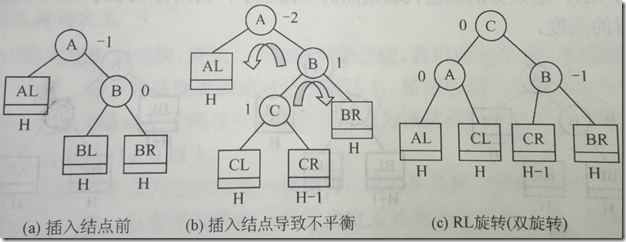
示例代码:

//先右后左旋转

    private Node RLRotate(Node node){

        //再进行右旋转

        RRotate(node.RChild);

        //再进行右旋

        return LRotate(node);

    }

插入操作

插入操作通过递归方式实现，在插入操作完成后需要对访问路径上的每个节点进行判断来确定是否要旋转。

public Node insert(Node node, int i){

        //先将节点插入到树中

        if(node == null)

            return new Node(i, 1, node);
    </span><span style="color: #008000">//</span><span style="color: #008000">插入的值与当前节点值进行比较来确定插入的位置</span>

    <span style="color: #0000ff">if</span>(i &lt;<span style="color: #000000"> node.val){

        node.LChild </span>=<span style="color: #000000"> insert(node.LChild, i);

        </span><span style="color: #008000">//</span><span style="color: #008000">判断是否进行调整</span>

        <span style="color: #0000ff">if</span>(height(node.LChild) - height(node.RChild) == 2<span style="color: #000000">){

            </span><span style="color: #0000ff">if</span>(i &lt;<span style="color: #000000"> node.LChild.val)

                </span><span style="color: #008000">//</span><span style="color: #008000">插入的节点在左孩子的左子树上，则需要进行右旋</span>

                node =<span style="color: #000000"> RRotate(node);

            </span><span style="color: #0000ff">else</span>

                <span style="color: #008000">//</span><span style="color: #008000">插入的节点在左孩子的右子树上，则需要先进行左旋后进行右旋</span>

                node =<span style="color: #000000"> LRRotate(node);

        }

    }

    </span><span style="color: #0000ff">else</span><span style="color: #000000">{

        node.RChild </span>=<span style="color: #000000"> insert(node.RChild, i);

        </span><span style="color: #0000ff">if</span>(height(node.LChild) - height(node.RChild) == -2<span style="color: #000000">){

            </span><span style="color: #0000ff">if</span>(i &gt;<span style="color: #000000"> node.RChild.val)

                node </span>=<span style="color: #000000"> LRotate(node);

            </span><span style="color: #0000ff">else</span><span style="color: #000000">

                node </span>=<span style="color: #000000"> RLRotate(node);

        }

    }

    node.height </span>= Math.max(height(node.LChild), height(node.RChild))+1<span style="color: #000000">;

    </span><span style="color: #0000ff">return</span><span style="color: #000000"> node;

}</span></pre></div>



//计算树的高度,主要解决空树高度的问题(空树的高度为0)

    private int height(Node node){

        return node == null ? 0:node.height;

    }

判断一棵树是否是AVL树

判断时通过后续遍历的方式来比较左右子树的高度差

static boolean isBalance(Node node,Depth d){

       if(node == null){

          d.height=0;

          return true;

       }

       Depth right=new Depth();

       Depth left = new Depth();

       if(isBalance(node.LChild,left)&&isBalance(node.RChild, right)){

           if(Math.abs(left.height - right.height)<2){//绝对值小于等于1

               //如果是平衡树，才有必要算深度，然后看上级是不是平衡树

              d.height=(left.height>right.height?left.height:right.height)+1;

              System.out.println("left="+left.height+" right="+right.height+" height"+d.height+" value="+node.val);

              return true;

           }

       }

       System.out.println("left="+left.height+" right="+right.height+" height"+d.height+" value="+node.val);

       return false;

    }
</span><span style="color: #0000ff">static</span> <span style="color: #0000ff">class</span><span style="color: #000000"> Depth{

    </span><span style="color: #0000ff">int</span><span style="color: #000000"> height;

}</span></pre></div>


完整代码

package com.dy.xidian;

public class AVL {


private Node root;


static class Node{


int val; //存储数据


int height; //权重


Node LChild; //右孩子


Node RChild; //左孩子
    <span style="color: #0000ff">public</span> Node(<span style="color: #0000ff">int</span> k, <span style="color: #0000ff">int</span><span style="color: #000000"> _height){

        </span><span style="color: #0000ff">this</span>.val =<span style="color: #000000"> k;

        </span><span style="color: #0000ff">this</span>. height =<span style="color: #000000"> _height;

    }

}

</span><span style="color: #0000ff">private</span> <span style="color: #0000ff">void</span> initAVL(<span style="color: #0000ff">int</span><span style="color: #000000">[] arr){

    </span><span style="color: #0000ff">for</span>(<span style="color: #0000ff">int</span><span style="color: #000000"> i : arr)

        root </span>=<span style="color: #000000"> insert(root, i);

}

</span><span style="color: #0000ff">public</span> AVL(<span style="color: #0000ff">int</span><span style="color: #000000">[] arr){

    initAVL(arr);

}

</span><span style="color: #008000">//</span><span style="color: #008000">右旋</span>

<span style="color: #0000ff">private</span><span style="color: #000000"> Node RRotate(Node node){

    Node A </span>=<span style="color: #000000"> node;

    Node B </span>=<span style="color: #000000"> node.LChild;

    </span><span style="color: #008000">//</span><span style="color: #008000">旋转</span>

    Node tmp =<span style="color: #000000"> B.RChild;

    B.RChild </span>=<span style="color: #000000"> A;

    A.LChild </span>=<span style="color: #000000"> tmp;

    </span><span style="color: #008000">//</span><span style="color: #008000">更新树的高度</span>

    A.height = Math.max(height(A.LChild), height(A.RChild))+1<span style="color: #000000">;

    B.height </span>= Math.max(height(B.LChild), height(B.RChild))+1<span style="color: #000000">;

    </span><span style="color: #0000ff">return</span><span style="color: #000000"> B;

}

</span><span style="color: #008000">//</span><span style="color: #008000">左旋</span>

<span style="color: #0000ff">private</span><span style="color: #000000"> Node LRotate(Node node){

    Node A </span>=<span style="color: #000000"> node;

    Node B </span>=<span style="color: #000000"> node.RChild;

    </span><span style="color: #008000">//</span><span style="color: #008000">旋转</span>

    Node tmp =<span style="color: #000000"> B.LChild;

    B.LChild </span>=<span style="color: #000000"> A;

    A.RChild </span>=<span style="color: #000000"> tmp;

    </span><span style="color: #008000">//</span><span style="color: #008000">更新树的高度</span>

    A.height = Math.max(height(A.LChild), height(A.RChild))+1<span style="color: #000000">;

    B.height </span>= Math.max(height(B.LChild), height(B.RChild))+1<span style="color: #000000">;

    </span><span style="color: #0000ff">return</span><span style="color: #000000"> B;

}

</span><span style="color: #008000">//</span><span style="color: #008000">先左后右旋转</span>

<span style="color: #0000ff">private</span><span style="color: #000000"> Node LRRotate(Node node){

    </span><span style="color: #008000">//</span><span style="color: #008000">先进行左旋</span>


LRotate(node.LChild);


//在进行右旋


return RRotate(node);


}
</span><span style="color: #008000">//</span><span style="color: #008000">先右后左旋转</span>

<span style="color: #0000ff">private</span><span style="color: #000000"> Node RLRotate(Node node){

    </span><span style="color: #008000">//</span><span style="color: #008000">再进行右旋转</span>


RRotate(node.RChild);


//再进行右旋


return LRotate(node);


}
</span><span style="color: #008000">//</span><span style="color: #008000">计算树的高度,主要解决空树高度的问题(空树的高度为0)</span>

<span style="color: #0000ff">private</span> <span style="color: #0000ff">int</span><span style="color: #000000"> height(Node node){

    </span><span style="color: #0000ff">return</span> node == <span style="color: #0000ff">null</span> ? 0<span style="color: #000000">:node.height;

}

</span><span style="color: #0000ff">public</span> Node insert(Node node, <span style="color: #0000ff">int</span><span style="color: #000000"> i){

    </span><span style="color: #008000">//</span><span style="color: #008000">先将节点插入到树中</span>

    <span style="color: #0000ff">if</span>(node == <span style="color: #0000ff">null</span><span style="color: #000000">)

        </span><span style="color: #0000ff">return</span> <span style="color: #0000ff">new</span> Node(i, 1<span style="color: #000000">);

    </span><span style="color: #008000">//</span><span style="color: #008000">插入的值与当前节点值进行比较来确定插入的位置</span>

    <span style="color: #0000ff">if</span>(i &lt;<span style="color: #000000"> node.val){

        node.LChild </span>=<span style="color: #000000"> insert(node.LChild, i);

        </span><span style="color: #008000">//</span><span style="color: #008000">判断是否进行调整</span>

        <span style="color: #0000ff">if</span>(height(node.LChild) - height(node.RChild) == 2<span style="color: #000000">){

            </span><span style="color: #0000ff">if</span>(i &lt;<span style="color: #000000"> node.LChild.val)

                </span><span style="color: #008000">//</span><span style="color: #008000">插入的节点在左孩子的左子树上，则需要进行右旋</span>

                node =<span style="color: #000000"> RRotate(node);

            </span><span style="color: #0000ff">else</span>

                <span style="color: #008000">//</span><span style="color: #008000">插入的节点在左孩子的右子树上，则需要先进行左旋后进行右旋</span>

                node =<span style="color: #000000"> LRRotate(node);

        }

    }

    </span><span style="color: #0000ff">else</span><span style="color: #000000">{

        node.RChild </span>=<span style="color: #000000"> insert(node.RChild, i);

        </span><span style="color: #0000ff">if</span>(height(node.LChild) - height(node.RChild) == -2<span style="color: #000000">){

            </span><span style="color: #0000ff">if</span>(i &gt;<span style="color: #000000"> node.RChild.val)

                node </span>=<span style="color: #000000"> LRotate(node);

            </span><span style="color: #0000ff">else</span><span style="color: #000000">

                node </span>=<span style="color: #000000"> RLRotate(node);

        }

    }

    node.height </span>= Math.max(height(node.LChild), height(node.RChild))+1<span style="color: #000000">;

    </span><span style="color: #0000ff">return</span><span style="color: #000000"> node;

}

</span><span style="color: #0000ff">public</span> <span style="color: #0000ff">static</span> <span style="color: #0000ff">void</span><span style="color: #000000"> main(String[] args) {

    </span><span style="color: #0000ff">int</span>[] arr = {1,2,3,4,5,6,7,8,9,10,11,12,13,14<span style="color: #000000">};

    AVL avl </span>= <span style="color: #0000ff">new</span><span style="color: #000000"> AVL(arr);

}


}

查考博文
http://blog.csdn.net/liyong199012/article/details/29219261








posted @

2016-11-03 16:52 

被罚站的树 

阅读(...) 

评论(...) 

编辑 

收藏

AVL树插入操作实现的更多相关文章

AVL树插入和删除
一.AVL树简介 AVL树是一种平衡的二叉查找树. 平衡二叉树(AVL 树)是一棵空树,或者是具有下列性质的二叉排序树: 1它的左子树和右子树都是平衡二叉树, 2且左子树和右子树高度之差的 ...
AVL树相关操作
#include <iostream> using namespace std; //AVL树的节点 template<typename T> class TreeNode { ...
AVL树插入(Python实现)
建立AVL树 class AVLNode(object): def __init__(self,data): self.data = data self.lchild = None self.rchi ...
avl树的操作证明
以下用大O表示节点,ABC表示三个集合. 仅分析左子树的情况,因为对称,右子树的情况一样. 插入节点前 O / \ O A / \ B C 插入节点后: O ...
AVL树Python实现
# coding=utf-8 # AVL树Python实现 def get_height(node): return node.height if node else -1 def tree_mini ...
树-二叉搜索树-AVL树
树-二叉搜索树-AVL树树树的基本概念节点的度:节点的儿子数树的度:Max{节点的度} 节点的高度:节点到各叶节点的最大路径长度树的高度:根节点的高度节点的深度(层数):根节点到该节点的路 ...
AVL树（平衡二叉树）
定义及性质 AVL树:AVL树是一颗自平衡的二叉搜索树. AVL树具有以下性质: 根的左右子树的高度只差的绝对值不能超过1 根的左右子树都是平衡二叉树(AVL树) 百度百科: 平衡二叉搜索树(Sel ...
AVL树的插入与删除
AVL 树要在插入和删除结点后保持平衡,旋转操作必不可少.关键是理解什么时候应该左旋.右旋和双旋.在Youtube上看到一位老师的视频对这个概念讲解得非常清楚,再结合算法书和网络的博文,记录如下. 1 ...
AVL树（查找、插入、删除）——C语言
AVL树平衡二叉查找树(Self-balancing binary search tree)又被称为AVL树(AVL树是根据它的发明者G. M. Adelson-Velskii和E. M. Land ...

随机推荐

[原]ubuntu14.04 网卡逻辑修改没有文件/etc/udev/rules.d/70-persistent-net.rules
-----问题出现------ 在新装的ubuntu14.04系统中没有发现文件/etc/udev/rule.d/70-persistent-net.rules, 无法修改网络的逻辑名称(即把第一张网 ...
如何在centos上安装epel源
一.EPEL是什么? EPEL (Extra Packages for Enterprise Linux,企业版Linux的额外软件包) 是Fedora小组维护的一个软件仓库项目,为RHEL/Cent ...
android：context,getApplicationContext()生命周期
getApplicationContext() 返回应用的上下文,生命周期是整个应用,应用摧毁它才摧毁Activity.this的context 返回当前activity的上下文,属于activity ...
linux-redhat6.4驱动无线网卡rtl8188eu
无线网卡Realtek Semiconductor Cop. RTL8188EUS 首先下载安装包: 其中的0BDA是Realtek的代码,8179是设备代码.从网上查到这个设备的芯片是rtl81 ...
Windows Azure Backup Agent安装注意事项
在Windows Server 2008 R2 SP1上安装Windows Azure Backup Agent时会出现错误: “Unable to execute the embedded appl ...
实现跨云应用——基于DNS的负载均衡
“公有云可以作为传统IT资源的延展,能帮助客户应对不断变化的需求”——这是我们在向客户介绍公有云产品时经常说的一句话.我们来看一个具体的需求: 某客户有一个web站点,部署在自有的数据中心(on-pr ...
ZooKeeper开发手册中文翻译（转）
本文Github地址:https://github.com/sundiontheway/zookeeper-guide-cn 本文假设你已经具有一定分布式计算的基础知识.你将在第一部分看到以下内容: ...
如何通过JQuery将DIV的滚动条滚动到指定的位置
这里有一个方法可以将DIV的滚动条滚动到其子元素所在的位置,方便自动定位. var container = $('div'), inner = $('#inner'); container.scrol ...
网格测地线算法（Geodesics in Heat）附源码
测地线又称为大地线,可以定义为空间曲面上两点的局部最短路径.测地线具有广泛的应用,例如在工业上测地线最短的性质就意味着最优最省,在航海和航空中,轮船和飞机的运行路线就是测地线.[Crane et al ...
KEngine：Unity3D资源的打包、加载、调试监控
资源模块做什么? 资源模块——ResourceModule,是KEngine中最核心的模块,其他模块基本或多或少的对它有依赖,它主要的功能是:资源打包.路径定义.资源管理.资源调试. 资源模块对Uni ...

AVL树插入操作实现

右单旋转

左单旋转

先左后右旋转

先右旋后左旋

插入操作

判断一棵树是否是AVL树

AVL树插入操作实现的更多相关文章

随机推荐

热门专题