C++版 - 剑指offer 面试题63：二叉搜索树的第k个结点(二叉树中序遍历的应用) 题解

面试题 63：二叉搜索树的第k个结点

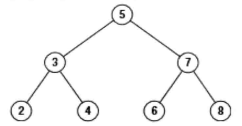
题目：给定一颗二叉搜索树，请找出其中的第k大的结点。例如， 5 / \ 3 7 /\ /\ 2 4 6 8 (见下面的图1) 中，按结点数值大小顺序第三个结点的值为4。

图1：一个有7个结点的二叉搜索树，如果按结点数值大小顺序输出，则第3个结点的值是4

提交网址： http://www.nowcoder.com/practice/ef068f602dde4d28aab2b210e859150a?tpId=13&tqId=11215

分析：

对于二叉搜索树BST，在树中任取一棵子树，其节点值都满足：左结点的值 < 父节点的值 < 右结点的值，故如果按照中序遍历的顺序遍历一棵二叉搜索树BST，遍历序列的数值是递增序的。只需要用中序遍历算法遍历一棵二叉搜索树BST，就可以找出它的第k大结点。非递归中序遍历加上计数器即可解决。

        6
     /     \
    3      8
  /  \     /  \
 2   5  7    9

非递归实现 AC代码：

#include<cstdio>
#include<vector>
#include<stack>
using namespace std;
struct TreeNode{
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};
class Solution {
public:
    TreeNode* KthNode(TreeNode* pRoot, unsigned int k)
    {
        TreeNode *p=pRoot;
        TreeNode *resNode;
		if(p==NULL || k==0)  return NULL;
		stack<TreeNode *> st;
		unsigned int count=0;

	while(!st.empty() || p != NULL)
	{
		if(p != NULL)
		{
			st.push(p);
			p=p->left;
		}
		if(p == NULL)
		{
			p=st.top();  // 取当前节点
			count++;
			if(count==k)  resNode=p;
			st.pop();
			p=p->right;
		}
	}
        return resNode;
    }
};

// 以下为测试
int main()
{
	Solution sol;
	TreeNode* root = new TreeNode(6);
	root->left = new TreeNode(3);
	root->left->left = new TreeNode(2);
	root->left->right = new TreeNode(5);
	root->right = new TreeNode(8);
	root->right->left = new TreeNode(7);
	root->right->right = new TreeNode(9);
	TreeNode* p=sol.KthNode(root, 3);
	printf("The value of Kth Node is: %d\n", p->val);
	return 0;
}

而提交同样作用的代码到牛客网OJ却报错了： control may reach end of non-void function [-Werror,-Wreturn-type， 本地在Visual Studio和Dev C++上都测试通过的...

意思好像是没有在函数最外层写统一的返回值，改了就AC了...

class Solution {
public:
    TreeNode* KthNode(TreeNode* pRoot, unsigned int k)
    {
        TreeNode *p=pRoot;
		if(p==NULL || k==0)  return NULL;
		stack<TreeNode *> st;
		unsigned int count=0;

	while(!st.empty() || p != NULL)
	{
		if(p != NULL)
		{
			st.push(p);
			p=p->left;
		}
		if(p == NULL)
		{
			p=st.top();  // 取当前节点
			count++;
			if(count==k)  return p;
			st.pop();
			p=p->right;
		}
	}
    }
};