清北学堂（2019 4 28 ） part 2

主要内容数据结构：

1.二叉搜索树

　　一棵二叉树，对于包括根节点在内的节点，所有该节点左儿子比此节点小，所有该节点右儿子比该节点大，（感觉好像二分...）

　　每个节点包含一个指向父亲的指针，和两个指向儿子的指针。如果没有则为空。每个节点还包含一个key值，代表他本身这个点的权值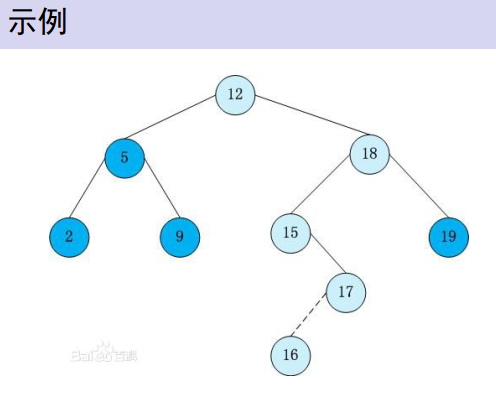

常用操作：

插入一个数，删除一个数，询问最大/最小值，询问第k大值。

插入操作：

现在我们要插入一个权值为x的节点。
为了方便，我们插入的方式要能不改变之前整棵树的形态。
首先找到根，比较一下key[root]和x,如果key[root] < x,节点应该插在root右侧，否则再左侧。看看root有没有右儿子，如果没有，那么直接把root的右儿子赋成x就完事了。
否则，为了不改变树的形态，我们要去右儿子所在的子树里继续这一操作，直到可以插入为止。

删除操作：

要删掉一个权值，首先要知道这个点在哪。

从root开始，像是插入一样找权值为x的点在哪。

定义x的后继y，是x右子树中所有点里，权值最小的点。
找这个点可以x先走一次右儿子，再不停走左儿子。
如果y是x的右儿子，那么直接把y的左儿子赋成原来x的左儿子，然后用y代替x的位置。

找第k大的数：

对每个节点在多记一个size[x]表示x这个节点子树里节点的个数。

从根开始，如果右子树的size ≥ k,就说明第k大值在右侧，往右边走。

如果右子树size + 1 = k,那么说明当前这个点就是第k大值。

否则，把k减去右子树size + 1,然后递归到左子树继续操作。

那么为什么呢？

证明：

　　由二叉搜索树性质可得，左边字数一定比其父节点小，右边则反之

　　看看正在处理的点的右子树根节点，对于其“size”，即节点个数，如果大于k，说明要找的树（或地址）肯定在右边

　　因为左边的恒比右边小，如果此时size>=k，说明右面至少还有k个没找过的数，我们要找的是第k大的数，并不能允许右边有多于k个比目标大的数，那么向右找

　　当找到当前节点的右子树根节点size+1=k时，说明这个数底下（包括自身）有k-1个比当前处理节点大的数，那么当前处理节点就是第k大的

　　如果没等找到size+1=k就size<k了怎么办？

　　说明右边比当前处理节点大的数并不足k，此时应向左找，找比当前节点小的数，也许时不时地向右子树找一下，最终找到第k大的数

　　（我因为仔细读问题，没看见第k“大”的数...当第k个（小）的数证的，百思不得其解...）

2.二叉堆

一只神仙提前讲过，我之前也整过，然而用的优先队列，因为对就是棵完全二叉树，（看题目，“二叉”堆吖~）

一直没有手写堆，今天试试。

代码：

#include<bits/stdc++.h>        //本代码致力于维护小根堆
using namespace std;
int a[100005];
int n;
int size;
inline void up(int t){         //把数据上浮
    while(a[t]<a[t>>1]&&t){
        swap(a[t],a[t>>1]);
        t>>=1;
    }
}
inline void down(int t){       //下沉
    while((t<<1)<=size){
        int l=t*2;
        int r=t*2+1;
        if(r>size){            //对于某些奇怪的只有左儿子的树的特判
            if(a[t]>a[l]){
                swap(a[t],a[l]);
                t=l;
            }
            break;
        }
        if(a[t]<=a[l]&&a[t]<=a[r])break;
        else if(a[l]<a[r]){    //判断把哪个儿子拿上来当爹
            swap(a[t],a[l]);
            t=l;
        }
        else{
            swap(a[t],a[r]);
            t=r;
        }
    }
}
inline void pop(){     //弹出堆顶
    swap(a[1],a[size]);
    size--;
    down(1);
}
inline void add(int now){ //添加新元素
    a[++size]=now;
    up(size);
}
int main(){
    scanf("%d",&n);
    while(n){
        n--;
        int x;
        scanf("%d",&x);
        add(x);
    }
    while(size){
        printf("%d ",a[1]);
        pop();
    }
    return 0;
}
p.s.我为了确保这玩意对，特意又交了一遍快排模板

（我写这玩意用了一晚上（并不怕笑话...），老师说下课时我差点脏话出口...我发誓这种情况不多见）

3.区间RMQ问题

举个例子（例题）：

给出一个序列，每次询问区间最大值.

看上去暴力模拟能过吖...

然而
N ≤ 100000, Q ≤ 1000000.

所以我们需要一套好算法，比如这个RMBRMQ，

主要思路是将总区间不断二分，根据这些区间进行计算，如图：

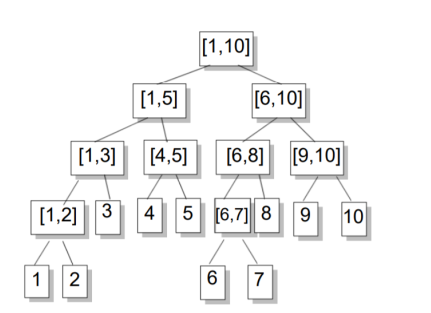
然后将所需访问区间拆分，但能保留的尽量大的区间一定要保留，因为大区间问问可以表示成许多小区间，只算大区间显然更快

延迟更新：

信息更新时，未必要真的做彻底的更新，可以只是将应该如何更新记录下来，等到真正需要查询准确信息时，才去更新 足以应付查询的部分。
在区间增加时，如果要加的区间正好覆盖一个节点，则增加其节 点的inc值和sum值，不再往下走.在区间询问时,还是采取正常的区间分解.
在上述两种操作中,如果我们到了区间[L, R]还要接着往下走,并且inc非0,说明子区间的信息是不对的,我们将inc传送到左儿子和右儿子上,并将inc赋成0，即完成了一次更新.

延迟更新可避免每次都赋值的麻烦情况，可极大省时

4.并查集

等我做出来村村通再整...

先整下按秩合并：

对每个顶点，再多记录一个当前整个结构中最深的点到根的深度deepx.
注意到两个顶点合并时,如果把比较浅的点接到比较深的节点上.
如果两个点深度不同，那么新的深度是原来较深的一个.
只有当两个点深度相同时，新的深度是原来的深度+1.
注意到一个深度为x的顶点下面至少有2x个点,所以x至多为log N.
那么在暴力向上走的时候,要访问的节点至多只有log个 。

然而路径压缩更好...虽有两种算法一起用的sao操作，但为了避免一种“玄学错误”（？？？）而并不这么用（起码用的肥肠少...）

5.树及LCA问题

在一棵有根树中,树上两点x, y的LCA指的是x, y向根方向遇到到第一个相同的点.
我们记每一个点到根的距离为deepx.
注意到x, y之间的路径长度就是deepx + deepy - 2 * deepLCA

两个点到根路径一定是前面一段不一样，（汇合）后面都一样.
注意到LCA的深度一定比x, y都要小.
利用deep，把比较深的点往父亲跳一格，直到x, y跳到同一个点上.
这样做复杂度是O(len).


首先不妨假设deepx < deepy.
为了后续处理起来方便，我们先把x跳到和y一样深度的地方.
如果x和y已经相同了,就直接退出.
否则,由于x和y到LCA的距离相同,倒着枚举步长,如果x, y的第2j个父亲不同，就跳上去.这样，最后两个点都会跳到离LCA距离为1的地方，在跳一步就行了.
时间复杂度O(N log N).

我..累了（QAQ）