PID控制器开发笔记之八：带死区的PID控制器的实现

　　在计算机控制系统中，由于系统特性和计算精度等问题，致使系统偏差总是存在，系统总是频繁动作不能稳定。为了解决这种情况，我们可以引入带死区的PID算法。

1、带死区PID的基本思想

　　带死区的PID控制算法就是检测偏差值，若是偏差值达到一定程度，就进行调节。若是偏差值较小，就认为没有偏差。用公式表示如下：

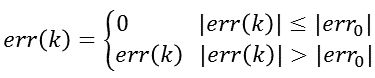
　　其中的死区值得选择需要根据具体对象认真考虑，因为该值太小就起不到作用，该值选取过大则可能造成大滞后。

　　带死区的PID算法，对无论位置型还是增量型的表达式没有影响，不过它是一个非线性系统。

　　除以上描述之外还有一个问题，在零点附近时，若偏差很小，进入死去后，偏差置0会造成积分消失，如是系统存在静差将不能消除，所以需要人为处理这一点。

2、算法实现

　　前面我们描述了带死区的PID控制的基本思想。在接下来我们来实现这一思想，同样是按位置型和增量型来分别实现。

（1）位置型PID算法实现

　　前面我们对微分项、积分项采用的不同的优化算法，他们都可以与死区一起作用于PID控制。这一节我们就来实现一个采用抗积分饱和、梯形积分、变积分算法以及不完全微分算法和死区控制的PID算法。首先依然是定义一个PID结构体。

 /*定义结构体和公用体*/
 
 typedef struct
 {
   float setpoint;               /*设定值*/
   float kp;                     /*比例系数*/
   float ki;                     /*积分系数*/
   float kd;                     /*微分系数*/
   float lasterror;              /*前一拍偏差*/
   float preerror;               /*前两拍偏差*/
   float deadband;               /*死区*/
   float result;                 /*PID控制器计算结果*/
   float output;                 /*输出值0-100%*/
   float maximum;                /*输出值上限*/
   float minimum;                /*输出值下限*/
   float errorabsmax;            /*偏差绝对值最大值*/
   float errorabsmin;            /*偏差绝对值最小值*/
   float alpha;                  /*不完全微分系数*/
   float derivative;              /*微分项*/
   float integralValue;          /*积分累计量*/
 }CLASSICPID;

　　接下来我们实现带死区、抗积分饱和、梯形积分、变积分算法以及不完全微分算法的增量型PID控制器。

 void PIDRegulator(CLASSICPID vPID,float pv)
 {
   float thisError;
   float result;
   float factor;
 
   thisError=vPID->setpoint-pv; //得到偏差值
   result=vPID->result;
 
   if (fabs(thisError)>vPID->deadband)
   {
     vPID-> integralValue= vPID-> integralValue+ thisError;
 
     //变积分系数获取
     factor=VariableIntegralCoefficient(thisError,vPID->errorabsmax,vPID->errorabsmin);
 
     //计算微分项增量带不完全微分
     vPID-> derivative =kd*(-vPID->alpha)* (thisError-vPID->lasterror +vPID->alpha*vPID-> derivative;
 
 result=vPID->kp*thisError+vPID->ki*vPID-> integralValue +vPID-> derivative;
   }
   else
   {
     if((abs(vPID->setpoint-vPID->minimum)<vPID->deadband)&&(abs(pv-vPID->minimum)<vPID->deadband))
     {
       result=vPID->minimum;
     }
   }
 
   /*对输出限值，避免超调和积分饱和问题*/
   if(result>=vPID->maximum)
   {
     result=vPID->maximum;
   }
 
   if(result<=vPID->minimum)
   {
     result=vPID->minimum;
   } 
 
   vPID->preerror=vPID->lasterror;  //存放偏差用于下次运算
   vPID->lasterror=thisError;
   vPID->result=result;
 
   vPID->output=((result-vPID->minimum)/(vPID->maximum-vPID->minimum))*100.0;
 }

（2）增量型PID算法实现

　　在位置型PID中我们实现了比较全面的PID控制器，对于增量型PID我们也相应的实现这样一个控制器。除了这些结合外，其他的优化算法也可以结合使用，可以根据具体的需要来实现。首先依然是定义一个PID结构体。

 /*定义结构体和公用体*/
 typedef struct
 {
   float setpoint;               /*设定值*/
   float kp;                     /*比例系数*/
   float ki;                     /*积分系数*/
   float kd;                     /*微分系数*/
   float lasterror;              /*前一拍偏差*/
   float preerror;               /*前两拍偏差*/
   float deadband;               /*死区*/
   float result;                 /*PID控制器计算结果*/
   float output;                 /*输出值0-100%*/
   float maximum;                /*输出值上限*/
   float minimum;                /*输出值下限*/
   float errorabsmax;            /*偏差绝对值最大值*/
   float errorabsmin;            /*偏差绝对值最小值*/
   float alpha;                  /*不完全微分系数*/
   float deltadiff;              /*微分增量*/
 }CLASSICPID;

　　接下来我们实现带死区、抗积分饱和、梯形积分、变积分算法以及不完全微分算法的增量型PID控制器。

 void PIDRegulator(CLASSICPID vPID,float pv)
 {
   float thisError;
   float result;
   float factor;
   float increment;
   float pError,dError,iError;
 
   thisError=vPID->setpoint-pv; //得到偏差值
   result=vPID->result;
 
   if (fabs(thisError)>vPID->deadband)
   {
     pError=thisError-vPID->lasterror;
     iError=(thisError+vPID->lasterror)/2.0;
     dError=thisError-*(vPID->lasterror)+vPID->preerror;
 
     //变积分系数获取
     factor=VariableIntegralCoefficient(thisError,vPID->errorabsmax,vPID->errorabsmin);
 
     //计算微分项增量带不完全微分
     vPID->deltadiff=kd*(-vPID->alpha)*dError+vPID->alpha*vPID->deltadiff;
 
     increment=vPID->kp*pError+vPID->ki*factor*iError+vPID->deltadiff;   //增量计算
   }
   else
   {
     if((fabs(vPID->setpoint-vPID->minimum)<vPID->deadband)&&(fabs(pv-vPID->minimum)<vPID->deadband))
     {
       result=vPID->minimum;
     }
     increment=0.0;
   }
 
   result=result+increment;
 
   /*对输出限值，避免超调和积分饱和问题*/
   if(result>=vPID->maximum)
   {
     result=vPID->maximum;
   }
 
   if(result<=vPID->minimum)
   {
     result=vPID->minimum;
   } 
 
   vPID->preerror=vPID->lasterror;  //存放偏差用于下次运算
   vPID->lasterror=thisError;
   vPID->result=result;
 
   vPID->output=((result-vPID->minimum)/(vPID->maximum-vPID->minimum))*100.0;
 }

3、总结

　　引入死区的主要目的是消除稳定点附近的波动，由于测量值的测量精度和干扰的影响，实际系统中测量值不会真正稳定在某一个具体的值，而与设定值之间总会存在偏差，而这一偏差并不是系统真实控制过程的反应，所以引入死区就能较好的消除这一点。

　　当然，死区的大小对系统的影响是不同的。太小可能达不到预期的效果，而太大则可能对系统的正常变化造成严重滞后，需要根据具体的系统对象来设定。

欢迎关注：