tensorflow--logistic regression
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
mnist=input_data.read_data_sets("tmp/data", one_hot=True) learning_rate=0.01
training_epochs=25
batch_size=100
display_step=1 # placeholder x,y 用来存储输入,输入图像x构成一个2维的浮点张量,[None,784]是简单的平铺图,'None'代表处理的批次大小,是任意大小
x=tf.placeholder(tf.float32,[None,784])
y=tf.placeholder(tf.float32,[None,10]) # variables 为模型定义权重和偏置
w=tf.Variable(tf.zeros([784,10]))
b=tf.Variable(tf.zeros([10])) pred=tf.nn.softmax(tf.matmul(x,w)+b) # w*x+b要加上softmax函数 # reduce_sum 对所有类别求和,reduce_mean 对和取平均
cost=tf.reduce_mean(-tf.reduce_sum(y*tf.log(pred),reduction_indices=1)) # 往graph中添加新的操作,计算梯度,计算参数的更新
optimizer=tf.train.GradientDescentOptimizer(learning_rate).minimize(cost) init=tf.initialize_all_variables() with tf.Session() as sess:
sess.run(init)
for epoch in range(training_epochs):
total_batch=int(mnist.train.num_examples/batch_size)
for i in range(total_batch):
batch_xs,batch_ys=mnist.train.next_batch(batch_size)
sess.run(optimizer,feed_dict={x:batch_xs,y:batch_ys})
if( epoch+1)%display_step==0:
print "cost=", sess.run(cost,feed_dict={x:batch_xs,y:batch_ys}) prediction=tf.equal(tf.argmax(pred,1),tf.argmax(y,1))
accuracy=tf.reduce_mean(tf.cast(prediction,tf.float32))
print "Accuracy:" ,accuracy.eval({x:mnist.test.image,y:mnist.test.labels})
logistic 函数:
二分类问题
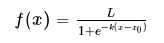
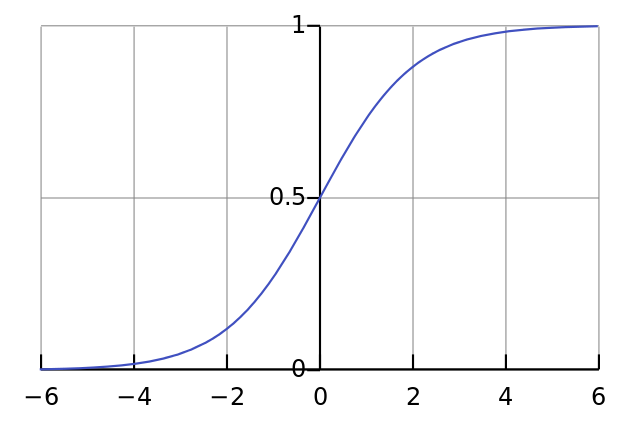
softmax 函数:
将k维向量压缩成另一个k维向量,进行多分类,logistic 是softmax的一个例外
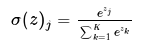
tensorflow--logistic regression的更多相关文章
- Linear and Logistic Regression in TensorFlow
Linear and Logistic Regression in TensorFlow Graphs and sessions TF Ops: constants, variables, funct ...
- 逻辑回归 Logistic Regression
逻辑回归(Logistic Regression)是广义线性回归的一种.逻辑回归是用来做分类任务的常用算法.分类任务的目标是找一个函数,把观测值匹配到相关的类和标签上.比如一个人有没有病,又因为噪声的 ...
- logistic regression与SVM
Logistic模型和SVM都是用于二分类,现在大概说一下两者的区别 ① 寻找最优超平面的方法不同 形象点说,Logistic模型找的那个超平面,是尽量让所有点都远离它,而SVM寻找的那个超平面,是只 ...
- Logistic Regression - Formula Deduction
Sigmoid Function \[ \sigma(z)=\frac{1}{1+e^{(-z)}} \] feature: axial symmetry: \[ \sigma(z)+ \sigma( ...
- SparkMLlib之 logistic regression源码分析
最近在研究机器学习,使用的工具是spark,本文是针对spar最新的源码Spark1.6.0的MLlib中的logistic regression, linear regression进行源码分析,其 ...
- [OpenCV] Samples 06: [ML] logistic regression
logistic regression,这个算法只能解决简单的线性二分类,在众多的机器学习分类算法中并不出众,但它能被改进为多分类,并换了另外一个名字softmax, 这可是深度学习中响当当的分类算法 ...
- Stanford机器学习笔记-2.Logistic Regression
Content: 2 Logistic Regression. 2.1 Classification. 2.2 Hypothesis representation. 2.2.1 Interpretin ...
- Logistic Regression vs Decision Trees vs SVM: Part II
This is the 2nd part of the series. Read the first part here: Logistic Regression Vs Decision Trees ...
- Logistic Regression Vs Decision Trees Vs SVM: Part I
Classification is one of the major problems that we solve while working on standard business problem ...
- Logistic Regression逻辑回归
参考自: http://blog.sina.com.cn/s/blog_74cf26810100ypzf.html http://blog.sina.com.cn/s/blog_64ecfc2f010 ...
随机推荐
- PWM实现ADC和DAC
一.PWM实现AD 利用普通单片机的2个IO及一个运算放大器即可实现AD转换电路,而且很容易扩展成多通道.其占用资源少,成本低,AD 转换精度可以达到8位甚至更高,因此具有一定的实用价值. 1.1 硬 ...
- 【165223&165218】结对感想——论如何与队友完美配合
★ 为什么要结对编程? 一.结对编程的优势 搭档的形式 平等.互补 高效率.共分享 相互影响.督促学习 方便复审与反馈 二.结对编程的方式 互换的角色 相同的目的 结对编程中有两个角色: (a)驾驶员 ...
- Go 语言和 Scala 语言对比
我在Google写过Go(自己的业余时间),也在LinkedIn写过Scala.两者都是具有一流的并发特性的现代语言. 下面的回答是基于我编写大规模的软件的经验得出. Go是一种开发模式严格固定,并且 ...
- Nginx宣布正式支持gRPC,附示例代码
原创 2018-03-20 薛命灯 聊聊架构 作者|Owen Garrett编辑|薛命灯 NGINX 官方博客正式宣布 NGINX 支持原生的 gPRC,现在就可以从代码仓库拉取快照版本.该特性将会被 ...
- js jquery数组去重
数组去重建议直接使用jquery的 $.unique(arr);方法,此外比较好的方法是本文中的unique3方法比较快用了一个hash表,就是所谓的空间换时间.本文还提供了很多其他写法,都是大同小异 ...
- ONI无法启动: Uh oh! Unable to launch Neovim...
问题描述 在终端中是可以打开nvim的,ONI无法正确找到位置 解决方法 修改配置文件,指定nvim的路径 终端中输入which nvim定位所在位置,这里返回的结果是/usr/local/bin/n ...
- 【洛谷P3901】数列找不同
题目大意:给定一个长度为 N 的序列,每个点被染了一个颜色.现有 M 个询问,每个询问查询区间 [l,r] 内的点是否颜色都是不同的. 题解:莫队裸题. 直接维护区间颜色数,用 cnt[] 记录下区间 ...
- java面试——多线程
背景:java知识比较宽泛,最好对每一类知识点进行分类总结,方便后面学习查看.该文主要用来总结多线程方面的知识点. 并发与并行的概念 并发性(concurrency)和并行性(parallel)是两个 ...
- 线程相关函数(1)-pthread_create(), pthread_join(), pthread_exit(), pthread_cancel() 创建取消线程
一. pthread_create() #include <pthread.h> int pthread_create(pthread_t *thread, const pthread_a ...
- ZooKeeper集群详细安装教程
1. 安装JDK 1.1 官网下载JDK 进入网址<a href="http://www.oracle.com/technetwork/java/javase/downloads/jd ...
