「HDU6158」 The Designer（圆的反演）

题目链接多校8-1009 HDU - 6158 The Designer

题意

T（<=1200）组，如图在半径R1、R2相内切的圆的差集位置依次绘制1,2,3,到n号圆，求面积之和（n<=1e7)。

题解

圆的反演：

（圆的反演就是半径为R，圆心O的圆为反演中心，点P的反演点就是在射线OP上满足\(|OP’|*|OP|=R^2\)的点P‘）

设切点为O，以O为圆心半径R的圆为反演点。将圆R1和R2反演得到两条直线，和两条直线相切的圆反演回去的圆就是1～n号圆的圆心。

那么它们的直径就是这些小圆的圆心和O的连线与小圆的交点反演回去的点的距离差。



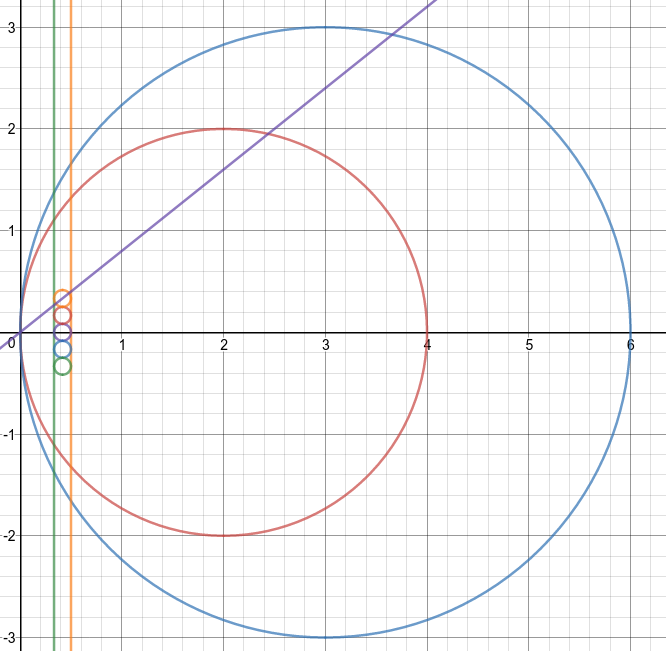
再扔一次画图工具Desmos

比赛的时候想到这里就以为复杂度太高，不知道怎么预处理。其实到后面圆面积会收敛得很快。精度只要1e-5,就可以及时break掉。

代码

#include <bits/stdc++.h>
using namespace std;
const double pi = acos(-1);
const double R = 1;
int t,r1,r2,n;
double r0,d,a,b,r,s;
double ans;
int main() {
    scanf("%d",&t);
    while(t--){
        scanf("%d%d%d",&r1,&r2,&n);
        if(r2<r1)swap(r1,r2);
        d=R*(r1+r2)/r2/r1/4;
        r0=d-R/2/r1;
        r=r2-r1;
        ans=pi*r*r;
        for(int i=1;i<=n/2;++i){
            a=sqrt(d*d+i*r0*i*r0*4)-r0,b=a+r0*2;
            r=(R/a-R/b)/2;
            s=pi*r*r;
            ans+=s;
            if(i*2<n)ans+=s;
            if(s*(n-i*2)<1e-6){
                break;
            }
        }
        printf("%.5f\n",ans);
    }
    return 0;
}