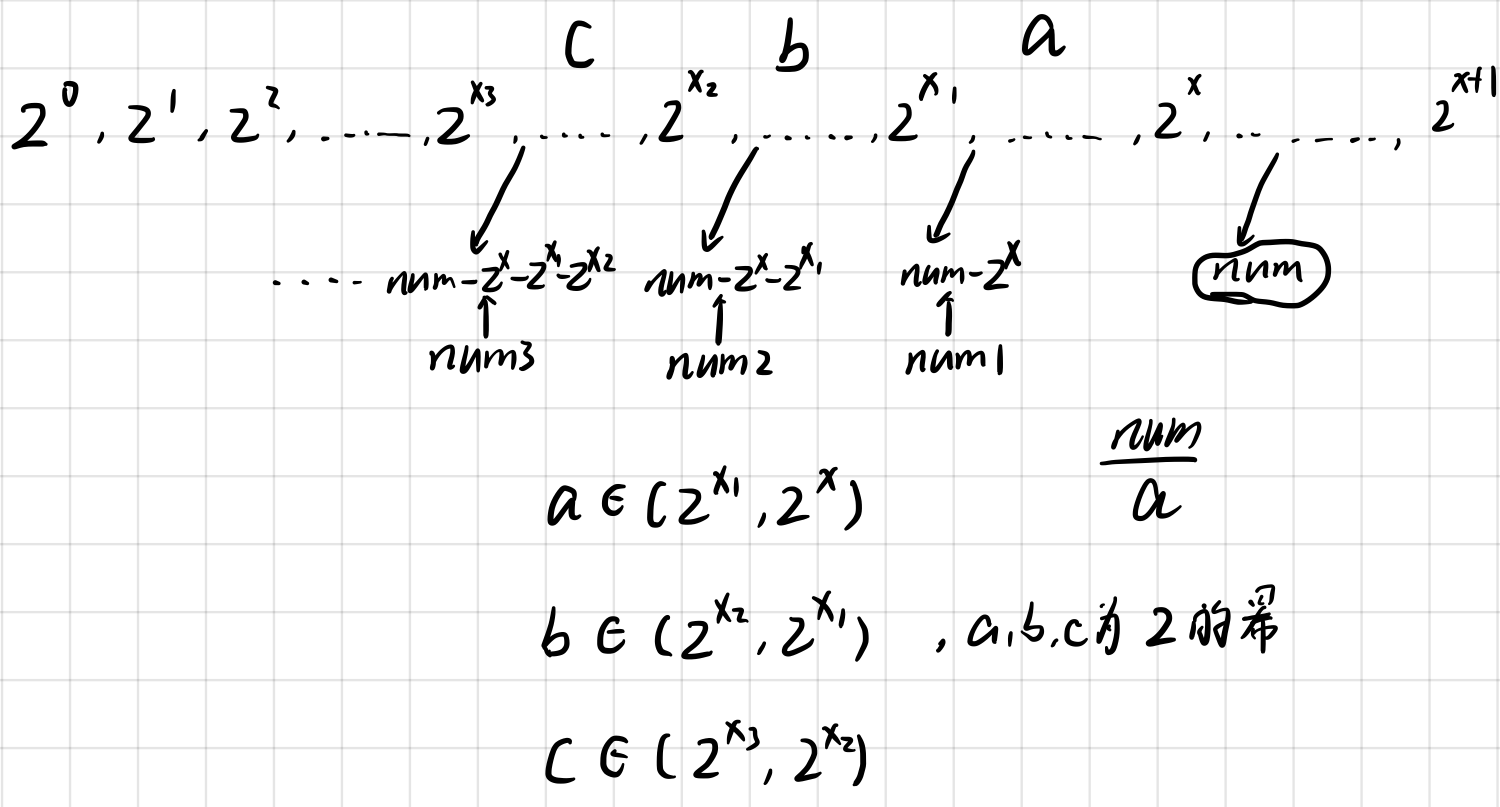Codeforces Round #529 (Div. 3) C. Powers Of Two(数学????)
•题意
给出一个整数 n ,问能否将 n 分解成 k 个数之和,且这 k 个数必须是 2 的幂。
如果可以,输出"YES",并打印出任意一组解,反之输出"NO";
•题解
预备知识补充:如何求出数 num 最少需要多少个 2的幂之和?
例如 :
num = 3 = 20+21至少需要两个
num = 4 = 22 至少需要一个
num = 17 = 24+20 至少需要两个
根据贪心的思想 :
令 2x ≤ num,求出最大的 x ,那么此时num可以表示为 num = 2x+num1 ( num1 = num-2x );
num1接着重复上述过程,求出 ≤num1 的最近的2x1,num1 = 2x1+num2 ( num2 = num1-2x1 );
那么num最少的2的幂之和就为 : 2x+2x1+2x2+.......;
如何求出x,x1,x2,......呢?
2x : ≤ num 的距num最近的2的幂
2x1 : ≤ num1 的距num1最近的2的幂
2x2 : ≤ num2 的距num2最近的2的幂
2x3 : ≤ num3 的距num3最近的2的幂
易得 :
(1) : num / 2x = oddNum , num / 2x1 = oddNum , num / 2x2 = oddNum ,......
(2) : num / a = evenNum , num / b = evenNum , num / c = evenNum ,........
(1)证明 :
num / 2x = 1;
num1 / 2x1 = 1 → (num-2x) / 2x1 = 1 → num / 2x1 - 2x / 2x1 = num / 2x1 - 2x-x1 = 1 → num / 2x1 = 1 + 2x-x1 = oddNum ( 奇+偶 );
num2 / 2x2 = 1 → (num-2x-2x1) / 2x2 = 1 → num / 2x1 - 2x / 2x2- 2x1 / 2x2 = 1 → num / 2x1 = 1 + 2x-x2+2x1-x2 = oddNum ( 奇+偶+偶 );
.................
(2)证明 :
num / a = (num1+2x) / a = num1 / a + 2x / a = 0+偶 = evenNum;( 2x1 ≤ num1 < a )
..................
所以说:
for i: to k
if(num/(^i)为奇数)
那么2^i就为num最少需要的2的幂之和的成员之一并且,$2^i$ 等价于 两个 $2^{i-1}$,所以,可以通过 $2^i$ 转化为 $2^{i-1}$ 开填充;
•Code
#include<iostream>
#include<cstdio>
using namespace std; int n,k;
int e[];//e[i] : num需要e[i]个2^i void Solve()
{
int curK=;
for(int i=;(<<i) <= n;++i)
if(n>>i&)
{
e[i]=;
curK++;
}
//最少需要curK个2的幂
if(k < curK || k > n)
{
printf("NO\n");
return ;
}
printf("YES\n");
for(int i=;~i;--i)
{
if(!e[i])
continue;
if(curK == k)
break;
int x=min(e[i],k-curK);
e[i] -= x;//减少x个2^i
e[i-] += *x;//增加2*x个2^(i-1)
curK += x;//比之前多了x个
}
for(int i=;i <= ;++i)
for(int j=;j < e[i];++j)
printf("%d ",<<i);
}
int main()
{
scanf("%d%d",&n,&k);
Solve();
return ;
}
•感悟
其实,在比赛时,并没有做出这道题,不过也有点小想法,还不成熟;
赛后看排名,无意间看到了hdu大神Claris的排名,然后,看了一下Claris的提交代码,哇,真简洁,
是我目前无法达到的。
大约花费了一个多小时的时间才理解了%%%%%%%%%%%%
分割线2019.5.23
重新温习了一下这道题;
假设 n 最少由 k 个2的幂组成:
n = 2x1 + 2x2 +.......+ 2xk;
那么 n / 2xi 为奇数;
今天重新想了一下这个,没有像之前那么繁琐的推公式,一想就想到;
如果 n / 2xi 为偶数,那么 2xi 可以变为 2xi+1 使得组成 n 这个幂值更大,那么,肯定比2xi所需的2的幂少,与假设矛盾;
再次分割2019.10.24
二进制思想;
十进制数 n 对应的二进制的第 i 位如果为 1,那么 $2^i$ 就是二进制转十进制 n 的组成部分;
那么,也即是说,n 对应的二进制有多少个 1,n 就至少需要多少个 2 的幂之和;
如果这些不够 k 个,那么就通过一个 $2^i$ 可以转化为两个 $2^{i-1}$ 的形式来增加幂之和的个数;
Codeforces Round #529 (Div. 3) C. Powers Of Two(数学????)的更多相关文章
- Codeforces Round #529 (Div. 3) C. Powers Of Two
http://codeforces.com/contest/1095/problem/C 题意:给n找出k个2的幂,加起来正好等于n.例如 9,4:9 = 1 + 2 + 2 + 4 思路:首先任何数 ...
- Codeforces Round #529 (Div. 3) C. Powers Of Two (二进制)
题意:给你一个数\(n\),问是否能有\(k\)个\(2\)次方的数构成,若满足,输出一种合法的情况. 题解:从高到低枚举二进制的每一位,求出\(n\)的二进制的\(1\)的位置放进优先队列中,因为\ ...
- # Codeforces Round #529(Div.3)个人题解
Codeforces Round #529(Div.3)个人题解 前言: 闲来无事补了前天的cf,想着最近刷题有点点怠惰,就直接一场cf一场cf的刷算了,以后的题解也都会以每场的形式写出来 A. Re ...
- Codeforces Round #529 (Div. 3) E. Almost Regular Bracket Sequence (思维)
Codeforces Round #529 (Div. 3) 题目传送门 题意: 给你由左右括号组成的字符串,问你有多少处括号翻转过来是合法的序列 思路: 这么考虑: 如果是左括号 1)整个序列左括号 ...
- Codeforces Round #368 (Div. 2) C. Pythagorean Triples(数学)
Pythagorean Triples 题目链接: http://codeforces.com/contest/707/problem/C Description Katya studies in a ...
- Codeforces Round #622 (Div. 2) B. Different Rules(数学)
Codeforces Round #622 (Div. 2) B. Different Rules 题意: 你在参加一个比赛,最终按两场分赛的排名之和排名,每场分赛中不存在名次并列,给出参赛人数 n ...
- Codeforces Round #284 (Div. 2)A B C 模拟 数学
A. Watching a movie time limit per test 1 second memory limit per test 256 megabytes input standard ...
- CodeForces Round #529 Div.3
http://codeforces.com/contest/1095 A. Repeating Cipher #include <bits/stdc++.h> using namespac ...
- Codeforces Round #529 (Div. 3) 题解
生病康复中,心情很不好,下午回苏州. 刷了一套题散散心,Div 3,全部是 1 A,感觉比以前慢了好多好多啊. 这几天也整理了一下自己要做的事情,工作上要努力... ... 晚上还是要认认真真背英语的 ...
随机推荐
- 微信小程序wxml無法實現頁面跳轉的問題
wxml的 navigator的url設置后無法跳轉? 檢查要跳轉的頁面是否是在APP.json的tabBar里註冊過,如果是tabBar頁面是不能用wx.navigateTo和wx.Redirect ...
- 四、Mysql主从同步
一.MySQL Replication介绍 MySQL Replication 官方文档 Replication可以实现将数据从一台数据库服务器(master)复制到一或多台数据库服务器(slave) ...
- commons-lang
今天在编码的过程中,对于null,采用==null进行判断.并且为了过滤"",使用了str.trim().length()==0,当str为null时,报空指针异常. 于是决定使用 ...
- window.onpopstate
概述 window.onpopstate是popstate事件在window对象上的事件句柄. 每当处于激活状态的历史记录条目发生变化时,popstate事件就会在对应window对象上触发. 如果当 ...
- hdu-1814(2-sat)
题意:给你n个组,m条规则,每组有俩个人,这两个人不能同时出现,然后m条规则代表着有两个人,这两个人也不能同时出现,问你是否存在每组都能出现一人的选择方案 解题思路:因为这个需要字典序输出,所以只能用 ...
- Facebook开源最先进的语音系统wav2letter++
最近,Facebook AI Research(FAIR)宣布了第一个全收敛语音识别工具包wav2letter++.该系统基于完全卷积方法进行语音识别,训练语音识别端到端神经网络的速度是其他框架的两倍 ...
- 前端es6基础语法
1.let.const.var var是声明全局的变量,作用域是全局,const是声明全局的常量,不能修改,而let是块级变量只在当前声明的作用域中生效: { var a = 10; let b = ...
- Cetos 中添加bbr服务
说明:此方法只适用于KVM架构的,OpenVZ平台无法使用: 一:安装bbr服务: # wget --no-check-certificate https://github.com/teddysun/ ...
- 给 Haproxy 创建日志文件
背景介绍:默认下的Haproxy配置是不会生成日志文件的,而无运行日志,无法确定系统运行是否流畅,无法提起预判可能发生的故障 创建Haproxy日志文件的步骤如下vi /etc/rsyslog.con ...
- 多项式细节梳理&模板(多项式)
基础 很久以前的多项式总结 现在的码风又变了... FFT和NTT的板子 typedef complex<double> C; const double PI=acos(-1); void ...