Codeforces 555C Case of Chocolate 其他

原文链接https://www.cnblogs.com/zhouzhendong/p/9272797.html

题目传送门 - CF555C

题意

　　给定一个 $n\times n(n\leq 10^9)$ 的方格阵列。

　　接下来，我们将从该方阵的副对角线开始进行一些操作。

　　操作 $"y\ x\ U"或"y\ x\ L"$ 分别表示一个人从第 $x$ 行第 $y$ 列开始走，$U$ 表示向上，$L$ 表示向左。保证初始位置在副对角线上面。

　　已经有人走过的不能再走，每次操作走到不能走为止。对于每次操作，输出能走几格。

　　下面是样例：

input

6 5
3 4 U
6 1 L
2 5 L
1 6 U
4 3 U

output

4
3
2
1
2

input

10 6
2 9 U
10 1 U
1 10 U
8 3 L
10 1 L
6 5 U

output

9
1
10
6
0
2

Note

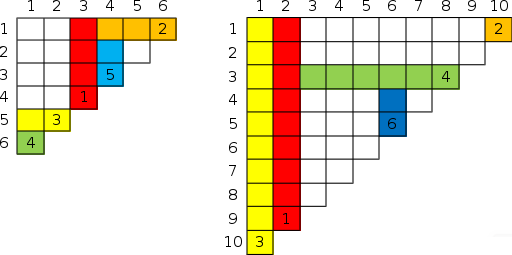
Pictures to the sample tests:

题解

　　由于向上和向左走是差不多的，所以我们这里只讲向上时的做法。

　　首先我们考虑特殊情况：

　　如果当前起始各自已经走过人了，那么输出 $0$ 。这个用 map 可以搞定。

　　对于向上的，我们在这个格子的左边分别找到离他最近的向上的和向左的行走记录。

　　考虑分两种情况讨论：

　　

　　

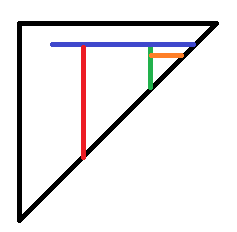
　　其中红色为当前位置，绿色为当前位置右侧第一个向上的记录。橙色为当前位置右侧的第一个向左记录。

　　蓝色为拦住绿色线段的线段。

　　这个只需要 set + lower_bound 就可以了。

　　代码还是比较短的。

代码

#include <bits/stdc++.h>
#define y1 __y1
using namespace std;
const int N=200005;
int n,q;
set <int> U,L;
map <int,int> u,l;
int main(){
	scanf("%d%d",&n,&q);
	U.clear(),L.clear(),u.clear(),l.clear();
	U.insert(0),L.insert(0);
	U.insert(n+1),L.insert(n+1);
	u[0]=l[0]=n+1,u[n+1]=l[n+1]=0;
	for (int i=1;i<=q;i++){
		int x,y;
		char ch[2];
		scanf("%d%d%s",&y,&x,ch);
		if (ch[0]=='L'){
			if (u[y]||l[x]){
				puts("0");
				continue;
			}
			int x1=*L.upper_bound(x),y1=n+1-x1;
			int y2=*--U.upper_bound(y),x2=n+1-y2;
			if (y1<y2)
				l[x]=x2-x;
			else
				l[x]=l[x1]+x1-x;
			printf("%d\n",l[x]);
			L.insert(x);
		}
		else {
			if (l[x]||u[y]){
				puts("0");
				continue;
			}
			int x1=*--L.upper_bound(x),y1=n+1-x1;
			int y2=*U.upper_bound(y),x2=n+1-y2;
			if (x1>x2)
				u[y]=y1-y;
			else
				u[y]=u[y2]+y2-y;
			printf("%d\n",u[y]);
			U.insert(y);
		}
	}
	return 0;
}