SVN快速入门笔记【转】

1. SVN版本控制软件目的

• 协作开发

• 远程开发

• 版本回退

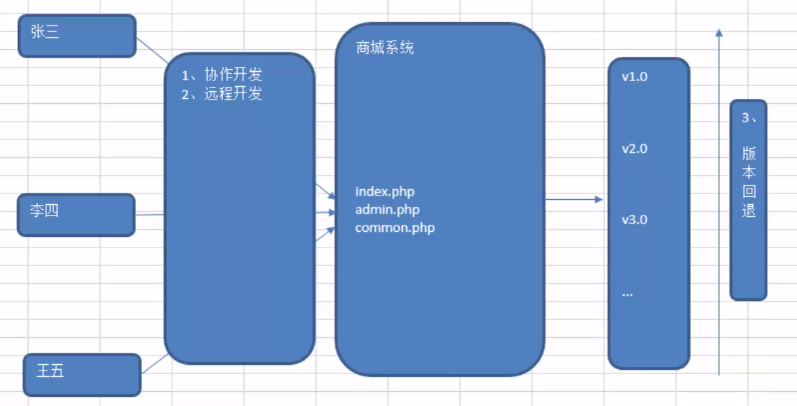
2. 什么是SVN

• subVersion

• 支持平台操作

• 支持版本回退

3. 获取SVN软件

属于C/S结构软件（客户端与服务端）

• server：VisualSVN

• client：Tortoisesvn

4. 使用SVN

4.1 将文件checkout到本地目录

• svn checkout path (path是服务器上的目录)

svn checkout svn://192.168.0.1/base/trunk/beamform-lz
svn co svn://192.168.0.1/base/trunk/beamform-lz  //简写

4.2 往版本库中添加新文件

• svn add file

svn add mycpp.cpp      // 添加mycpp.cpp
svn add ./pro/*.cpp    // 添加pro文件夹下所有cpp文件

4.3 将改动的文件提交到版本库

• svn commit -m "mycomment"  [-N][--no-unlock] PATH (如果选择了保持锁,就使用--no-unlock)

svn commit -m "change test.cpp add fun" test.cpp
svn ci -m "change test.cpp add fun" test.cpp  // 简写

4.4 加锁/解锁

• svn lock -m "lockInfo" [--force] PATH

svn lock -m "lock test file" test.cpp
svn unlock PATH   // 解锁

4.5 更新到某个版本

• svn update -r 版本号 path

svn update   //如果后面没有目录，默认将当前目录以及子目录下的所有文件都更新到最新的版本
svn update -r  test.cpp  // 将版本库中的文件test.cpp还原到版本10
svn update test.cpp        //更新，于版本库同步。如果提交的时候提示过期的话，是因为冲突，需要先update, 修改文件，然后清除svn resolved ,最后再提交commit
svn up                     //简写

4.6 查看文件或者目录状态

• svn status path    (目录下的文件和子目录的状态，正常状态不显示)

• svn status -v path (显示文件和子目录状态)

第一列保持相同，第二列显示工作版本号，第三和第四列显示最后一次修改的版本号和修改人

svn status
svn diff
svn revert
简写: svn st

4.7 删除文件

• svn delete path/file -m "delete test.cpp"

svn delete test.cpp  ==>  svn ci -m "delete test.cpp"  //推荐这种
svn del(rm/remove)   //简写

4.8 查看日志

• svn log path

svn log test.cpp   //显示这个文件的所有修改记录，及其版本好的变化

4.9 查看文件详细信息

• svn info path

svn info test.cpp

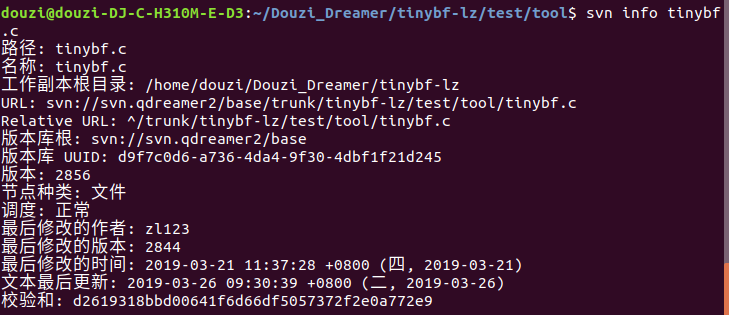
4.10 比较差异

• svn diff path (将修改的文件与基础版本比较)

svn diff test.cpp

• svn diff -r m:n path(对版本m和版本n比较差异)

svn diff -r : test.cpp
svn di    //简写

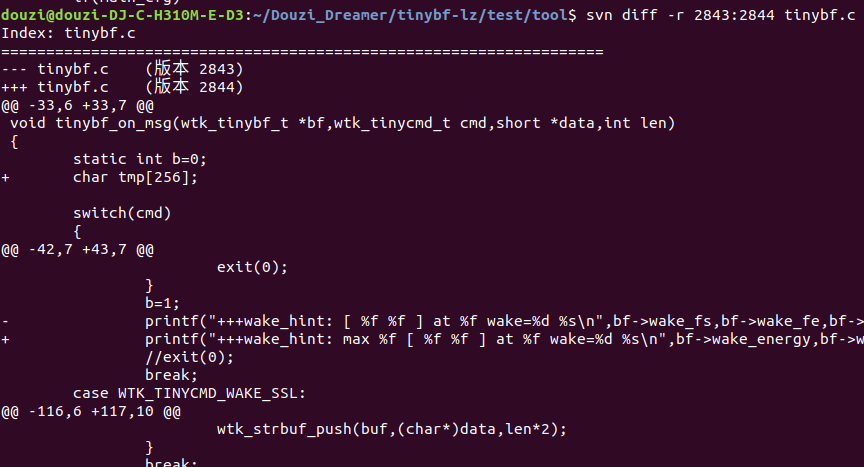
4.11 将两个版本之间的差异合并到当前文件

• svn merge -r m:n path

svn merge -r  : test.cpp  //将版本2043与2044之间的差异合并到当前文件，但是一般都会产生冲突，需要处理一下

4.12 svn帮助

svn help
svn help ci

5. 遇到问题

5.1 解决冲突

• svn resolved：移除工作副本的目录或文件的“冲突”状态

svn resolved

摘抄自：https://www.cnblogs.com/puloieswind/p/6150432.html

用来复习笔记，侵删