cf869C组合计数问题

如果在两个区域里连点，两个区域内选的点数一定要相等

即a中选出i个点，必须与b中选出i个点相连

连接种类数为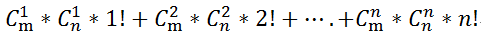 

然后我们再来看，如果ab中有两点相连，其中一点再与c相连会出事吗？

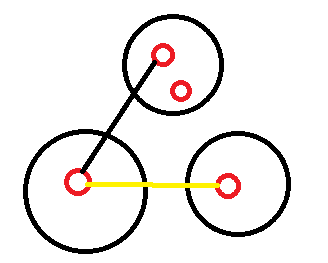
很显然不会对答案产生任何影响

所以我们可以得出另外一个结论

a-b b-c c-a所连的边无论如何都是两两独立的

也就是说，如果a-b连边的可能数为x，b-c连边的可能数为y，c-a连边的可能数为z

#include<bits/stdc++.h>
using namespace std;
#define maxn 5005
#define mod 998244353
#define ll long long
ll n,a,b,c,ans1,ans2,ans3;
ll C[maxn][maxn],f[maxn];
void init(){
    memset(C,,sizeof C);
    f[]=f[]=;
    for(int i=;i<=;i++)f[i]=f[i-]*i%mod;
    for(int i=;i<=;i++)C[i][]=C[i][i]=;
    for(int i=;i<=;i++)
        for(int j=;j<i;j++)
            C[i][j]=(C[i-][j]+C[i-][j-])%mod;
}
int main(){
    init();
    cin>>a>>b>>c;
    int k=min(a,b);
    for(int i=;i<=k;i++)
        ans1=(ans1+(f[i]*C[a][i]%mod)*C[b][i])%mod;
    k=min(b,c);
    for(int i=;i<=k;i++)
        ans2=(ans2+(f[i]*C[b][i]%mod)*C[c][i])%mod;
    k=min(c,a);
    for(int i=;i<=k;i++)
        ans3=(ans3+(f[i]*C[a][i]%mod)*C[c][i])%mod;
    cout<<(ans1*ans2)%mod*ans3%mod<<endl;
}