Noip模拟8 2021.6.17

T1 星际旅行

仔细一看，发现像一个欧拉路（简称一笔画）。

满足“可以一笔画”的条件是：

1.所有点都有偶数条连边;

2.有偶数个点连奇数条边;

满足以上两个条件的任意一个即可一笔画。

然而还要保证图的联通性。就是说如果有一个图，有一些点是孤立的，按照题意也是可行的。但是如果图像是两个不同的区域，每个区域的点互不连

这种情况就是假的，直接输出零。

因为双向边，我们不妨把每条边看作有两条。那么满足题目情况有三种：

1.去掉任意两个自环;

2.去掉一个自环和任意一条边;

3.去掉连在一个点上的任意两条边;

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4 const int NN=100005;
 5 int n,m,cnt,ans,out[NN];
 6 bool vis[NN];
 7 struct SNOW{int to,next;}; SNOW e[NN<<1]; int r[NN<<1],tot;
 8 inline void add(int x,int y){e[++tot]=(SNOW){y,r[x]}; r[x]=tot;}
 9 inline void dfs(int x){
10     vis[x]=true;
11     for(int i=r[x];i;i=e[i].next)
12         if(!vis[e[i].to]) dfs(e[i].to);
13 }
14 namespace WSN{
15     inline int main(){
16         scanf("%lld%lld",&n,&m);
17         for(int i=1,x,y;i<=m;i++){
18             scanf("%lld%lld",&x,&y);
19             if(x==y) {cnt++;continue;}
20             add(x,y); add(y,x);
21             out[x]++; out[y]++;
22         }
23         ans+=cnt*(cnt-1)/2+cnt*tot/2;
24         for(int i=1;i<=n;i++) if(out[i]) {dfs(i);break;}
25         if(!tot) {cout<<0<<endl; return 0;}
26         for(int i=1;i<=n;i++) if(!vis[i] && out[i]){cout<<0<<endl; return 0;}
27         for(int i=1;i<=n;i++) ans+=out[i]*(out[i]-1)/2;
28         printf("%lld\n",ans);
29         return 0;
30     }
31 }
32 signed main(){return WSN::main();}

T2 砍树

一看这题发现暴力很好打，就飞快得抡了一发暴力上去，但是循环范围开小了（重点是后来不知咋的发现好像没有排序的必要，把排序delete掉了），所以真正的暴力能拿到10分，然而在打暴力时发现二分并无正确性（因为没有单调性，可能每四天比每五天优，而第六天比第四天更优，这也是我第一层循环到头不停的理由），然而二分却能拿到30。。。。小马瞬间meng bi 好吧

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4 const int NN=101;
 5 int n,K,tr[NN],ans;
 6 namespace WSN{
 7     inline int main(){
 8         scanf("%lld%lld",&n,&K);
 9         for(int i=1;i<=n;i++) scanf("%lld",&tr[i]);
10         sort(tr+1,tr+n+1);
11         for(int i=1;i<=tr[1]+K;i++){
12             int tmp=0,vis[NN]={};
13             for(int j=i;j<=tr[1]+K;j+=i){
14                 for(int k=1;k<=n;k++){
15                     if(tr[k]<=j && !vis[k]){
16                         tmp+=j-tr[k];
17                         vis[k]=true;
18                     }
19                     if(tmp>K) break;
20                 }
21                 if(tmp>K) break;
22             }
23             if(tmp<K) ans=i;
24         }
25         printf("%lld\n",ans);
26         return 0;
27     }
28 }
29 signed main(){return WSN::main();}

可以对拍的正确暴力

然而正解是推一个柿子：

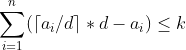
预处理一个：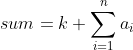

则柿子转化为：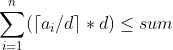

看出这是一个天花板函数，图像很好画，他的每一定值区域的最右端点就是天数的最优解（用右端点坐标结论），还要满足小于等于sum

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4 const int NN=101;
 5 int n,K,tr[NN],ans,tot,l,r;
 6 inline bool judge(int d){
 7     int cnt=0;
 8     for(int i=1;i<=n;i++) cnt+=ceil((double)tr[i]/d);
 9     if(cnt*d>tot) return 0;
10     else return 1;
11 }
12 namespace WSN{
13     inline int main(){
14         scanf("%lld%lld",&n,&K);
15         for(int i=1;i<=n;i++) scanf("%lld",&tr[i]),tot+=tr[i];
16         tot+=K;
17         for(l=1;l<=tot;l=r+1){
18             r=tot/(tot/l);
19             if(judge(r)) ans=r;
20         }
21         printf("%lld\n",ans);
22         return 0;
23     }
24 }
25 signed main(){return WSN::main();}

T3 超级树

一看题，看不懂，考场上打了个预处理就跳走了，拿了个小点儿分，当时想着估计是个dp，后来也没多想，光看第四题有无问题了，结果。。。

设dp[i][j]表示i_超级树有j条点不重复路径的方案数。考虑dp[1]对dp[i+1]的贡献。

首先设l表示左子树的合法路径条数，r同理。记录一个num=dp[i][l]*dp[i][r]。

有非常容易想到的几种情况：

1.什么也不做 dp[i+1][l+r]+=num
2.根自己作为一条新路径 dp[i+1][l+r+1]+=num
3.根连接到左子树(或右子树)的某条路径上 dp[i+1][l+r]+=2*num*(l+r)
4.根连接左子树和右子树的各一条路径 dp[i+1][l+r-1]+=2*num*l*r
5.根连接左子树(或右子树)的两条路径 dp[i+1][l+r-1]+=num*(l*(l-1)+r*(r-1))

起始：dp[1][0]=dp[1][1]=1;

目标：dp[k][1];

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4 int k,p,dp[301][301];
 5 namespace WSN{
 6     inline int main(){
 7         scanf("%lld%lld",&k,&p);
 8         dp[1][0]=dp[1][1]=1;
 9         for(int i=0;i<k;i++)
10             for(int j=0;j<k;j++)
11                 for(int l=0;l<=j;l++){
12                     int r=j-l,num=dp[i][l]*dp[i][r]%p;
13                     dp[i+1][l+r]=(dp[i+1][l+r]+num+2*num*(l+r))%p;
14                     dp[i+1][l+r+1]=(dp[i+1][l+r+1]+num)%p;
15                     dp[i+1][l+r-1]=(dp[i+1][l+r-1]+num*(l*(l-1)+r*(r-1))+2*num*l*r)%p;
16                 }
17         printf("%lld\n",dp[k][1]);
18         return 0;
19     }
20 }
21 signed main(){return WSN::main();}

T4 求和

本次考试败点，傻der的一批

一看第四题，挺可做的，（前提是前二道题抡上部分分，第三题不太可做），就是lca板子忘了，不过好说，还有dfs，可以暴力求解，但是太慢了怎么办，可以特判几种情况加速：

1.有一个点是1，直接找爹推到根;

2.x=y，直接快速幂

3.如果x，y深度一样，lca就是他们上一层。。。。。。（哎，我当时咋没有举出反例呢？多组数据查询，好，于是就这样爆零了）

样例里不是满二叉树，这样的话3情况是假的无法可知，试了样例中树的各种lca，就是没换一个树试试，然后就痛失100分呗。

再就是lca板子一直打的是在线算法，四个函数，倍增处理循环还贼麻烦，要是当时打雨天的尾巴用树链剖分或者树上倍增，就不用费劲特判了

哎，还是做题的时候要好好做，用一些自己背过的板子。。。。草

这里给出树上倍增的lca

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4 inline int read(){
 5     int x=0,f=1; char ch=getchar();
 6     while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
 7     while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
 8     return x*f;
 9 }
10
11 const int NN=3000005,p=998244353;
12 int n,m,d[NN],f[NN][20],t;
13 queue<int> q;
14 struct SNOW{int to,next;}; SNOW e[NN<<1]; int r[NN<<1],tot;
15 inline void add(int x,int y){e[++tot]=(SNOW){y,r[x]}; r[x]=tot;}
16 inline int qmo(int a,int b){
17     int ans=1; a%=p;
18     while(b){
19         if(b&1) ans=(ans*a)%p;
20         b>>=1; a=(a*a)%p;
21     } return ans;
22 }
23 inline void bfs(){
24     q.push(1); d[1]=0;
25     while(!q.empty()){
26         int x=q.front(); q.pop();
27         for(int i=r[x];i;i=e[i].next){
28             int y=e[i].to;
29             if(y==1||d[y]) continue;
30             d[y]=d[x]+1;
31             f[y][0]=x;
32             for(int j=1;j<=t;j++)
33                 f[y][j]=f[f[y][j-1]][j-1];
34             q.push(y);
35         }
36     }
37 }
38 inline int lca(int x,int y){
39     if(x==1||y==1) return 1;
40     if(d[x]>d[y]) swap(x,y);
41     for(int i=t;i>=0;i--)
42         if(d[f[y][i]]>=d[x]) y=f[y][i];
43     if(x==y) return x;
44     for(int i=t;i>=0;i--)
45         if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
46     return f[x][0];
47 }
48 namespace WSN{
49     inline int main(){
50         n=read();
51         for(int i=1,x,y;i<n;i++){
52             x=read(),y=read();
53             add(x,y); add(y,x);
54         }
55         t=(int)(log(n)/log(2))+1;
56         bfs();
57         m=read();
58         while(m--){
59             int x=read(),y=read(),z=read();
60             int LCA=lca(x,y),ans=0;
61             for(int i=d[LCA];i<=d[x];i++) ans=(ans+qmo(i,z))%p;
62             for(int i=d[LCA]+1;i<=d[y];i++) ans=(ans+qmo(i,z))%p;
63             printf("%lld\n",ans);
64         }
65         return 0;
66     }
67 }
68 signed main(){return WSN::main();}